
假期復習第九天―――等差、等比數列的性質,數列求和
一.這幾個性質你掌握了嗎?請回顧一遍:
1.等差數列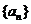 的任意連續
的任意連續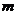 項的和構成的數列
項的和構成的數列 仍為等差數列.
仍為等差數列.
2.等差數列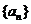 中,若
中,若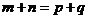 ,則
,則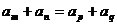
3.等比數列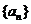 中,若
中,若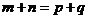 ,則
,則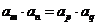
4.等比數列{an}的任意連續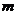 項的和構成的數列
項的和構成的數列 仍為等比數列.
仍為等比數列.
5.兩個等差數列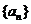 與
與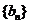 的和差的數列
的和差的數列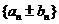 仍為等差數列.
仍為等差數列.
6.兩個等比數列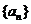 與
與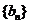 的積、商、倒數的數列
的積、商、倒數的數列 、
、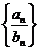 、
、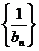 仍為等比數列.
仍為等比數列.
7.運用倒序相加、錯位相減、拆項相消等重要的數學方法進行求和運算。
二.特別要注意下列方法:
1.解決等差數列和等比數列的問題時,通常考慮兩類方法:①基本量法:即運用條件轉化為關于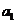 和
和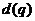 的方程;②巧妙運用等差數列和等比數列的性質,一般地運用性質可以化繁為簡,減少運算量.
的方程;②巧妙運用等差數列和等比數列的性質,一般地運用性質可以化繁為簡,減少運算量.
2.求數列的和注意方法的選取:關鍵是看數列的通項公式; 求和過程中注意分類討論思想的運用;
三.下列習題你必須掌握:
1.各項都是正數的等比數列{ }的公比q≠1,且
}的公比q≠1,且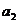 ,
, ,
,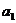 成等差數列,則
成等差數列,則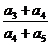 的值為( )
的值為( )
A.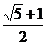 B.
B.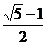 C.
C.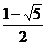 D.
D.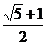 或
或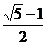
解析: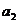 ,
, ,
,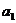 成等差數列得到了關于首項和公差的關系,帶入到所求式子可以減少未知數。
成等差數列得到了關于首項和公差的關系,帶入到所求式子可以減少未知數。
2.設等差數列{an}的前n項的和為Sn,若a1>0,S4=S8,則當Sn取得最大值時,n的值為
A.5 B.
3.設數列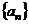 是等差數列,且
是等差數列,且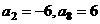 ,
,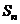 是數列
是數列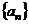 的前
的前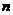 項和,則( )
項和,則( )
A、 B、
B、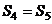 C、
C、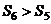 D、
D、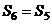
解析:2,3兩道題都要用函數的思想來解決,注意到等差數列的前n項和是關于n的二次函數,找出對稱軸。
4.若一等數列的前7項的和為48, 前14項的和為72, 則它的前21項的和為 ( )
A. 96 B.
5.已知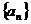 為等比數列,
為等比數列, ,
,
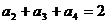 ,那么,
,那么,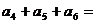 。
。
6.求下列數列的前n項和:
(1)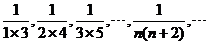 ;
;
(2)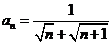 ;
;
(3)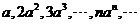 ;
;
7.已知數列{an}為等差數列,公差d≠0,其中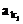 ,
,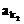 ,…,
,…,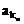 恰為等比數列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
恰為等比數列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com