
題目列表(包括答案和解析)
11 (文)命題“若
(文)命題“若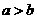 ,則
,則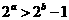 ”的否命題為
”的否命題為

(理)如果橢圓的對稱軸為坐標軸,短軸的一個端點與兩焦點組成一正三角形,焦點在y軸上,且a-c=,
那么橢圓的方程是

12 (文)
(文)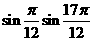 的值是
的值是

(理)函數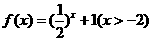 的反函數
的反函數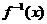 是
是
13 (文)如果橢圓的對稱軸為坐標軸,短軸的一個端點與兩焦點組成一正三角形,焦點在y軸上,且a-c=,
那么橢圓的方程是
(文)如果橢圓的對稱軸為坐標軸,短軸的一個端點與兩焦點組成一正三角形,焦點在y軸上,且a-c=,
那么橢圓的方程是 
(理)已知直線ax+by+c=0被圓M: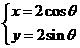 所截得的弦AB的長為
所截得的弦AB的長為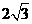 ,那么
,那么
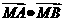 的值等于
的值等于

14 已知直線ax+by+c=0被圓M:
已知直線ax+by+c=0被圓M: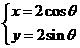 所截得的弦AB的長為
所截得的弦AB的長為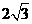 ,那么
,那么
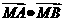 的值等于
的值等于

15 已知函數
已知函數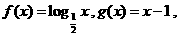 設
設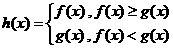 ,則使
,則使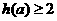 成立的
成立的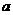 的范圍是
的范圍是

16 有 以下幾個命題
有 以下幾個命題
①曲線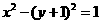 按
按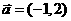 平移可得曲線
平移可得曲線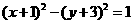 ;
;
②若|x|+|y|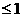 ,則使x+y取得最大值和最小值的最優解都有無數多個;
,則使x+y取得最大值和最小值的最優解都有無數多個;
③設A、B為兩個定點,為常數 ,
,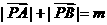 ,則動點P的軌跡為橢圓;
,則動點P的軌跡為橢圓;
④若橢圓的左、右焦點分別為F1、F2,P是該橢圓上的任意一點,則點F2關于“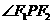 的外角平分線”的對稱點M的軌跡是圓
的外角平分線”的對稱點M的軌跡是圓
其中真命題的序號為
;(寫出所有真命題的序號)
1 設集合P={直線的傾斜角},Q={兩個向量的夾角},R={兩條直線的夾角},M={直線l1到l2的角}則必有
設集合P={直線的傾斜角},Q={兩個向量的夾角},R={兩條直線的夾角},M={直線l1到l2的角}則必有
A Q
Q R=P
R=P M
B
M
B R
R M
M P
P Q
Q
C Q=R
Q=R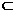 M=P
D
M=P
D R
R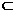 P
P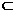 M
M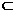 Q
Q
2 在等差數列
在等差數列 中,若
中,若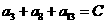 ,則其前n項和
,則其前n項和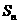 的值等于5C的是
的值等于5C的是
A
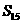 B
B
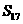 C
C
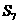 D
D
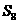
3 (文)若點B分
(文)若點B分 的比為
的比為 ,且有
,且有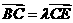 ,則
,則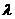 等于
等于
A 2
B
2
B
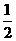 C
C 1
D
1
D -1
-1
(理)函數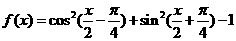 是
是
A 周期為
周期為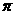 的奇函數
B
的奇函數
B 周期為
周期為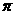 的偶函數
的偶函數
C 周期為
周期為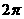 的奇函數
D
的奇函數
D 周期為
周期為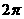 的偶函數
的偶函數
4 過點(-4,0)作直線L與圓x2+y2+2x-4y-20=0交于A、B兩點,如果|AB|=8,
過點(-4,0)作直線L與圓x2+y2+2x-4y-20=0交于A、B兩點,如果|AB|=8,
則L的方程為
A 5x+12y+20=0
B
5x+12y+20=0
B 5x-12y+20=0
5x-12y+20=0
C 5x-12y+20=0或x+4=0
D
5x-12y+20=0或x+4=0
D 5x+12y+20=0或x+4=0
5x+12y+20=0或x+4=0
5 (文)已知p,
q, p+q是等差數列,p ,q ,pq是等比數列,則橢圓
(文)已知p,
q, p+q是等差數列,p ,q ,pq是等比數列,則橢圓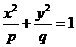 的準線方程是
的準線方程是
A
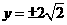 B
B
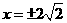 C
C
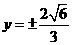 D
D
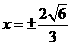
(理)已知命題P:關于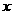 的不等式
的不等式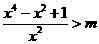 的解集為
的解集為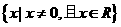 ;命題Q:
;命題Q: 是減函數
是減函數 若P或Q為真命題,P且Q為假命題,則實數
若P或Q為真命題,P且Q為假命題,則實數 的取值范圍是
的取值范圍是
A (1,2)
B
(1,2)
B
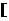 1,2)
C
1,2)
C (-
(- ,1
,1 D
D (-
(- ,1)
,1)
6 (文)已知命題P:關于
(文)已知命題P:關于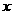 的不等式
的不等式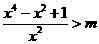 的解集為
的解集為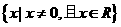 ;命題Q:
;命題Q: 是減函數
是減函數 若P或Q為真命題,P且Q為假命題,則實數
若P或Q為真命題,P且Q為假命題,則實數 的取值范圍是
的取值范圍是
A (1,2)
B
(1,2)
B
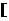 1,2)
C
1,2)
C (-
(- ,1
,1 D
D (-
(- ,1)
,1)
(理)若點B分 的比為
的比為 ,且有
,且有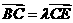 ,則
,則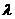 等于
等于
A 2
B
2
B
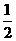 C
C 1
D
1
D -1
-1
7 (文)函數
(文)函數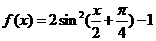 是
是
A 周期為
周期為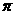 的奇函數
B
的奇函數
B 周期為
周期為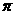 的偶函數
的偶函數
C 周期為
周期為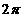 的奇函數
D
的奇函數
D 周期為
周期為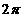 的偶函數
的偶函數
(理)若 ,對任意實數
,對任意實數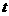 都有
都有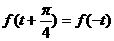 ,且
,且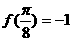 , 則實數
, 則實數 的值等于
的值等于
A
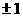 B
B
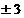 C
C -3或1 D
-3或1 D -1或3
-1或3
8 (文)若
(文)若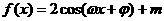 ,對任意實數
,對任意實數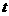 都有
都有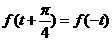 ,且
,且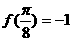 , 則實數
, 則實數 的值等于
的值等于
A
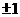 B
B
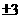 C
C -3或1 D
-3或1 D -1或3
-1或3
(理)設函數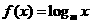 ,數列
,數列 是公比為
是公比為 的等比數列,若
的等比數列,若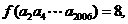 則
則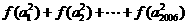 的值等于
的值等于
A -1974
B
-1974
B -1990
C
-1990
C 2022
D
2022
D 2038
2038
9 (文)設函數
(文)設函數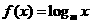 ,數列
,數列 是公比為
是公比為 的等比數列,若
的等比數列,若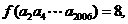 則
則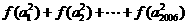 的值等于
的值等于
A -1974
B
-1974
B -1990
C
-1990
C 2022
D
2022
D 2038
2038
(理)函數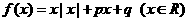 是奇函數,且在R上是增函數的充要條件是
是奇函數,且在R上是增函數的充要條件是
A p>0 ,q=0
B
p>0 ,q=0
B p<0 ,q=0 C
p<0 ,q=0 C p≤0,q=0 D
p≤0,q=0 D p≥0,q=0
p≥0,q=0
10 (文)函數
(文)函數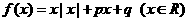 是奇函數,且在R上是增函數的充要條件是
是奇函數,且在R上是增函數的充要條件是
A p>0 ,q=0
B
p>0 ,q=0
B p<0 ,q=0 C
p<0 ,q=0 C p≤0,q=0 D
p≤0,q=0 D p≥0,q=0
p≥0,q=0
(理)已知函數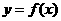 滿足:①
滿足:①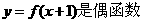 ;②在
;②在 上為增函數
上為增函數
若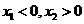 ,且
,且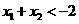 ,則
,則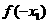 與
與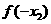 的大小關系是
的大小關系是
A
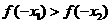 B
B
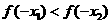
C
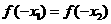 D
D 無法確定
無法確定
第Ⅱ卷 (非選擇題,共100分)
1 第Ⅱ共6頁,用藍、黑色的鋼筆或圓珠筆直接答在試卷中
第Ⅱ共6頁,用藍、黑色的鋼筆或圓珠筆直接答在試卷中
2 答卷前,請將密封線內的項目填寫清楚
答卷前,請將密封線內的項目填寫清楚
21、(I)當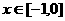 時,
時,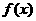 上的點P(
上的點P(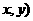 與
與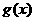 上的點Q(
上的點Q(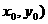
關于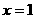 對稱,則
對稱,則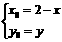 此時
此時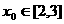 代入
代入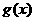
得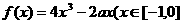 )
)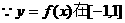 上是偶函數
上是偶函數
 當
當 時,
時,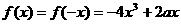
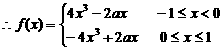 ………………………………5分
………………………………5分
(II)命題條件等價于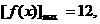 因為
因為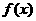 為偶函數,所以只需考慮
為偶函數,所以只需考慮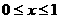 的情況.
的情況.
求導
由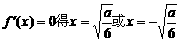 (舍)…………………………8分
(舍)…………………………8分
①當0<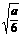 <1,即
<1,即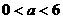 時
時
 |
0 |
(0,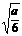 ) ) |
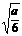 |
(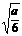 ,1) ,1) |
1 |
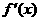 |
|
+ |
|
- |
|
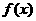 |
0 |
 |
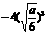 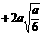 |
 |
-4+2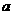 |
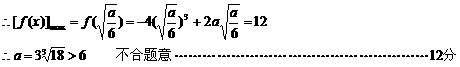
②當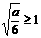 ,即
,即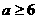 時,
時,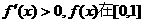 上單調遞增
上單調遞增

綜上,存在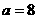 使得
使得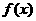 的圖象的最高點在直線
的圖象的最高點在直線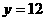 上.……………14分
上.……………14分
21. (本小題滿分14分)
設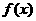 是定義在[-1,1]上的偶函數,
是定義在[-1,1]上的偶函數,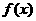 ,
,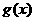 的圖象關于直線
的圖象關于直線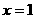 對稱,且當
對稱,且當
x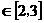 時,
時,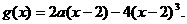
(1)求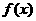 的表達式;
的表達式;
(2)是否存在正實數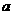 ,使函數
,使函數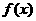 的圖象的最高點在直線
的圖象的最高點在直線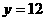 上,若存在,求出正實數
上,若存在,求出正實數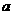 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
20. (本小題滿分14分)
函數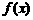 的定義域為R,并滿足以下條件:
的定義域為R,并滿足以下條件:
①對任意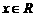 ,有
,有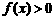 ;
;
②對任意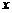 、
、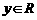 ,有
,有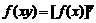 ;
;
③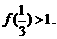
(Ⅰ)求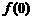 的值;
的值;
(Ⅱ)求證: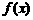 在R上是單調增函數;
在R上是單調增函數;
(Ⅲ)若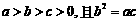 ,求證:
,求證: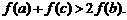
解法一:(1)令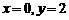 ,得:
,得: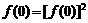

(2)任取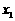 、
、 ,且
,且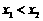 .設
.設 則
則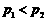
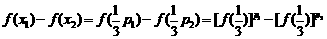
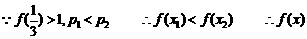 在R上是單調增函數
在R上是單調增函數
(3)由(1)(2)知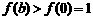
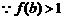
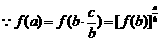
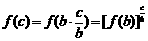
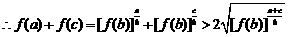
而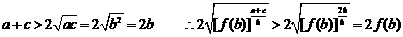
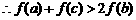
解法二:(1)∵對任意x、y∈R,有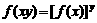
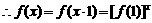
∴當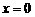 時
時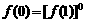
∵任意x∈R, 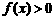
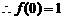
(2)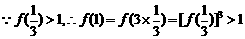
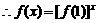 是R上單調增函數
即
是R上單調增函數
即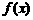 是R上單調增函數;
是R上單調增函數;
(3)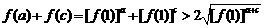
而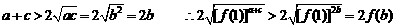
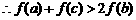
19. (本小題滿分14分)
已知f (x)=x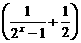 ,
,
(1) 證明:f (x)>0;
(2) 設F(x)=f(x+t)-f (x-t) (t≠o),試判斷F(x)的奇偶性。
解:(1) 函數f (x)的定義域是{x| x∈R且x≠0}, 且f (-x)=(-x)·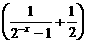 =f (x),
=f (x),
∴ f (x)是偶函數。當x>0時, 2x>1, 2x-1>0, ∴ f (x)>0,
當x<0時, -x>0, f (x)=f (-x)>0, ∴ 對所有定義域內的x的值,都有f (x)>0.
(2) F(-x)=f (-x+t)-f (-x-t)=f (x-t)-f (x+t)=-F(x), ∴ 函數是奇函數。
18. (本小題滿分14分)
統計表明,某種型號的汽車在勻速行駛中每小時耗油量y(升)關于行駛速度x(千米/小時)的函數解析式可以表示為:y=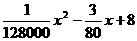 (0<x≤120).已知甲、乙兩地相距100千米。
(0<x≤120).已知甲、乙兩地相距100千米。
(Ⅰ)當汽車以40千米/小時的速度勻速行駛時,從甲地到乙地要耗油多少升?
(Ⅱ)當汽車以多大的速度勻速行駛時,從甲地到乙地耗油最少?最少為多少升?
解:(I)當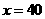 時,汽車從甲地到乙地行駛了
時,汽車從甲地到乙地行駛了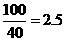 小時,
小時,
要耗沒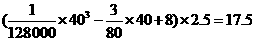 (升)。
(升)。
答:當汽車以40千米/小時的速度勻速行駛時,從甲地到乙地耗油17.5升。
(II)當速度為 千米/小時時,汽車從甲地到乙地行駛了
千米/小時時,汽車從甲地到乙地行駛了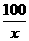 小時,設耗油量為
小時,設耗油量為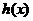 升,
升,
依題意得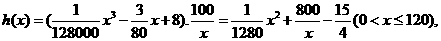
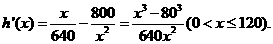
令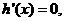 得
得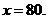
當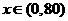 時,
時,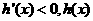 是減函數;
是減函數;
當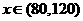 時,
時,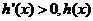 是增函數。
是增函數。
 當
當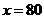 時,
時,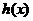 取到極小值
取到極小值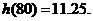
因為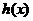 在
在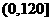 上只有一個極值,所以它是最小值。
上只有一個極值,所以它是最小值。
答:當汽車以80千米/小時的速度勻速行駛時,從甲地到乙地耗油最少,最少為11.25升。
17.(本小題滿分12分)
若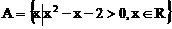 ,
,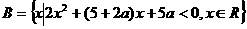 ,
,
且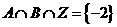 ,其中Z為整數集,求實數
,其中Z為整數集,求實數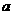 的取值范圍。
的取值范圍。
解:.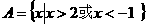 ,
,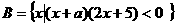 (………………2分)
(………………2分)
(1)當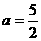 時,
時,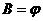 不符合題意.(…………………5分)
不符合題意.(…………………5分)
(2)當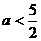 時,
時, 得
得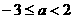 (……………………9分)
(……………………9分)
(3)當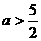 時,
時,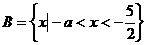 不符合題意。(…………………12分)
不符合題意。(…………………12分)
綜上所得 (…………………14)
(…………………14)
16.(本題滿分12分)
解:(1)1,37 (2)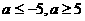
16.(本小題滿分12分)
已知函數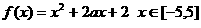
(1)當a=-1時,求函數f (x)的最大值和最小值.
(2)求實數a的取值范圍,使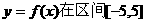 上是單調函數.
上是單調函數.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com