
題目列表(包括答案和解析)
已知數列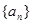 的前n項和
的前n項和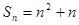 ,數列
,數列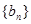 有
有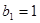 ,
,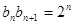
(1)求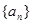 的通項;
的通項;
(2)若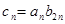 ,求數列
,求數列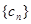 的前n項和
的前n項和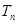 .
.
【解析】第一問中,利用當n=1時,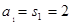
當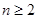 時,
時,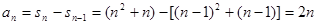
得到通項公式
第二問中,∵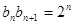 ∴
∴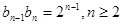 ∴數列
∴數列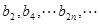 是以2為首項,2為公比的等比數列,利用錯位相減法得到。
是以2為首項,2為公比的等比數列,利用錯位相減法得到。
解:(1)當n=1時,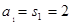 ……………………1分
……………………1分
當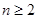 時,
時,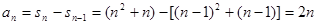 ……4分
……4分
又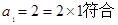
∴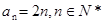 ……………………5分
……………………5分
(2)∵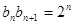 ∴
∴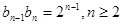
∴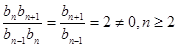 ……………………7分
……………………7分
又∵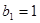 ,
,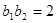 ∴
∴ 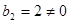
∴數列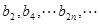 是以2為首項,2為公比的等比數列,
是以2為首項,2為公比的等比數列,
∴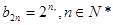 ……………………9分
……………………9分
∴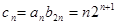
∴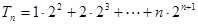 ①
①
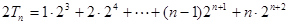 ②
②
①-②得: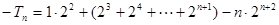
∴
已知二項式
(1)當n=4時,寫出該二項式的展開式;
(2)若展開式的前三項的二項式系數的和等于79,則展開式中第幾項的二項式系數最大?
設![]() 是各項均不為零的等差數列
是各項均不為零的等差數列![]() ,且公差
,且公差![]() ,若將此數列刪去某一項得到的數列(按原來的順序)是等比數列。
,若將此數列刪去某一項得到的數列(按原來的順序)是等比數列。
(1)當n=4時,求![]() 的數值;w.w.w.k.s.5.u.c.o.m
的數值;w.w.w.k.s.5.u.c.o.m ![]()
(2)求n的所有可能值。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com