
題目列表(包括答案和解析)
已知數(shù)列 的前
的前 項和為
項和為 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通項公式;
的通項公式;
(Ⅱ) 設(shè) (
( N*).
N*).
①證明:  ;
;
② 求證: .
.
【解析】本試題主要考查了數(shù)列的通項公式的求解和運用。運用 關(guān)系式,表示通項公式,然后得到第一問,第二問中利用放縮法得到
關(guān)系式,表示通項公式,然后得到第一問,第二問中利用放縮法得到 ,②由于
,②由于 ,
,
所以 利用放縮法,從此得到結(jié)論。
利用放縮法,從此得到結(jié)論。
解:(Ⅰ)當 時,由
時,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
從而有 ,與
,與 矛盾,所以
矛盾,所以 .
.
從而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①證明:
證法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
證法二: ,下同證法一.
……10分
,下同證法一.
……10分
證法三:(利用對偶式)設(shè) ,
, ,
,
則 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因為
,又因為 ,所以
,所以 .即
.即
 ………10分
………10分
證法四:(數(shù)學歸納法)①當 時,
時,  ,命題成立;
,命題成立;
②假設(shè) 時,命題成立,即
時,命題成立,即 ,
,
則當 時,
時,

 即
即
即
故當 時,命題成立.
時,命題成立.
綜上可知,對一切非零自然數(shù) ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
從而 .
.
也即
設(shè)f (x)=sin 2x+ (sin x-cos x)(sin x+cos x),其中x∈R.
(sin x-cos x)(sin x+cos x),其中x∈R.
(Ⅰ) 該函數(shù)的圖象可由
 的圖象經(jīng)過怎樣的平移和伸縮變換得到?
的圖象經(jīng)過怎樣的平移和伸縮變換得到?
(Ⅱ)若f (θ)= ,其中
,其中 ,求cos(θ+
,求cos(θ+ )的值;
)的值;
【解析】第一問中,
即 變換分為三步,①把函數(shù)
變換分為三步,①把函數(shù) 的圖象向右平移
的圖象向右平移 ,得到函數(shù)
,得到函數(shù) 的圖象;
的圖象;
②令所得的圖象上各點的縱坐標不變,把橫坐標縮短到原來的 倍,得到函數(shù)
倍,得到函數(shù) 的圖象;
的圖象;
③令所得的圖象上各點的橫坐標不變,把縱坐標伸長到原來的2倍,得到函數(shù) 的圖象;
的圖象;
第二問中因為 ,所以
,所以 ,則
,則 ,又
,又
 ,
, ,從而
,從而
進而得到結(jié)論。
(Ⅰ) 解:
即 。…………………………………3分
。…………………………………3分
變換的步驟是:
①把函數(shù) 的圖象向右平移
的圖象向右平移 ,得到函數(shù)
,得到函數(shù) 的圖象;
的圖象;
②令所得的圖象上各點的縱坐標不變,把橫坐標縮短到原來的 倍,得到函數(shù)
倍,得到函數(shù) 的圖象;
的圖象;
③令所得的圖象上各點的橫坐標不變,把縱坐標伸長到原來的2倍,得到函數(shù) 的圖象;…………………………………3分
的圖象;…………………………………3分
(Ⅱ) 解:因為 ,所以
,所以 ,則
,則 ,又
,又
 ,
, ,從而
,從而 ……2分
……2分
(1)當 時,
時, ;…………2分
;…………2分
(2)當 時;
時;
若函數(shù)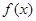 在定義域內(nèi)存在區(qū)間
在定義域內(nèi)存在區(qū)間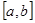 ,滿足
,滿足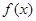 在
在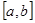 上的值域為
上的值域為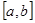 ,則稱這樣的函數(shù)
,則稱這樣的函數(shù)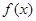 為“優(yōu)美函數(shù)”.
為“優(yōu)美函數(shù)”.
(Ⅰ)判斷函數(shù)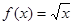 是否為“優(yōu)美函數(shù)”?若是,求出
是否為“優(yōu)美函數(shù)”?若是,求出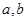 ;若不是,說明理由;
;若不是,說明理由;
(Ⅱ)若函數(shù)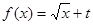 為“優(yōu)美函數(shù)”,求實數(shù)
為“優(yōu)美函數(shù)”,求實數(shù)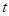 的取值范圍.
的取值范圍.
【解析】第一問中,利用定義,判定由題意得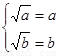 ,由
,由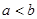 ,所以
,所以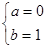
第二問中, 由題意得方程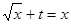 有兩實根
有兩實根
設(shè)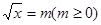 所以關(guān)于m的方程
所以關(guān)于m的方程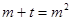 在
在 有兩實根,
有兩實根,
即函數(shù)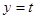 與函數(shù)
與函數(shù)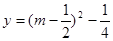 的圖像在
的圖像在 上有兩個不同交點,從而得到t的范圍。
上有兩個不同交點,從而得到t的范圍。
解(I)由題意得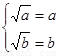 ,由
,由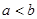 ,所以
,所以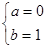 (6分)
(6分)
(II)由題意得方程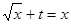 有兩實根
有兩實根
設(shè)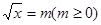 所以關(guān)于m的方程
所以關(guān)于m的方程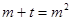 在
在 有兩實根,
有兩實根,
即函數(shù)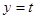 與函數(shù)
與函數(shù)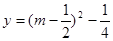 的圖像在
的圖像在 上有兩個不同交點。
上有兩個不同交點。
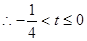
設(shè)數(shù)列 的各項均為正數(shù).若對任意的
的各項均為正數(shù).若對任意的 ,存在
,存在 ,使得
,使得 成立,則稱數(shù)列
成立,則稱數(shù)列 為“Jk型”數(shù)列.
為“Jk型”數(shù)列.
(1)若數(shù)列 是“J2型”數(shù)列,且
是“J2型”數(shù)列,且 ,
, ,求
,求 ;
;
(2)若數(shù)列 既是“J3型”數(shù)列,又是“J4型”數(shù)列,證明:數(shù)列
既是“J3型”數(shù)列,又是“J4型”數(shù)列,證明:數(shù)列 是等比數(shù)列.
是等比數(shù)列.
【解析】1)中由題意,得 ,
, ,
, ,
, ,…成等比數(shù)列,且公比
,…成等比數(shù)列,且公比 ,
,
所以.
(2)中證明:由{ }是“j4型”數(shù)列,得
}是“j4型”數(shù)列,得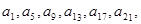 ,…成等比數(shù)列,設(shè)公比為t. 由{
,…成等比數(shù)列,設(shè)公比為t. 由{ }是“j3型”數(shù)列,得
}是“j3型”數(shù)列,得
 ,…成等比數(shù)列,設(shè)公比為
,…成等比數(shù)列,設(shè)公比為 ;
;
 ,…成等比數(shù)列,設(shè)公比為
,…成等比數(shù)列,設(shè)公比為 ;
;
 …成等比數(shù)列,設(shè)公比為
…成等比數(shù)列,設(shè)公比為 ;
;
如圖,四棱柱 中,
中,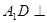 平面
平面 ,底面
,底面 是邊長為
是邊長為 的正方形,側(cè)棱
的正方形,側(cè)棱 .
.

(1)求三棱錐 的體積;
的體積;
(2)求直線 與平面
與平面 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一點
上存在一點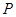 ,使得
,使得 ,當二面角
,當二面角 的大小為
的大小為 時,求實數(shù)
時,求實數(shù) 的值.
的值.
【解析】(1)在 中,
中,
 .
(3’)
.
(3’)
(2)以點D為坐標原點,建立如圖所示的空間直角坐標系 ,則
,則
 (4’)
(4’)
 ,設(shè)平面
,設(shè)平面 的法向量為
的法向量為 ,
,
由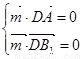 得
得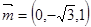 ,
(5’)
,
(5’)
則 ,
,
 . (7’)
. (7’)
(3)
設(shè)平面 的法向量為
的法向量為 ,由
,由 得
得 ,
(10’)
,
(10’)

國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com