
題目列表(包括答案和解析)
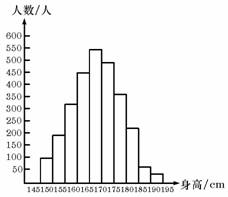
上面左圖是某縣參加2007年高考的學生身高條形統(tǒng)計圖,從左到右的各條形表示的學生人數(shù)依次記為A1、A2、…、A10(如A2表示身高(單位:cm)(150,155)內(nèi)的學生人數(shù)).右圖是統(tǒng)計左圖中身高在一定范圍內(nèi)學生人數(shù)的一個算法流程圖.現(xiàn)要統(tǒng)計身高在160~180cm(含160cm,不含180cm)的學生人數(shù),那么在流程圖中的判斷框內(nèi)應填寫的條件是( )
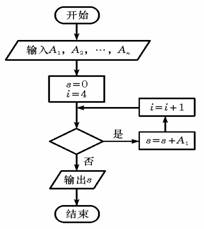 A.i<6 B. i<7 C. i<8 D. i<9
A.i<6 B. i<7 C. i<8 D. i<9
第二部分 非選擇題(共100分)
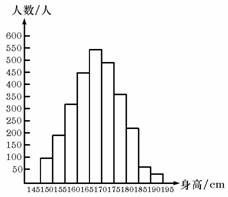
上面左圖是某縣參加2007年高考的學生身高條形統(tǒng)計圖,從左到右的各條形表示的學生人數(shù)依次記為A1、A2、…、A10(如A2表示身高(單位:cm)(150,155)內(nèi)的學生人數(shù)).右圖是統(tǒng)計左圖中身高在一定范圍內(nèi)學生人數(shù)的一個算法流程圖.現(xiàn)要統(tǒng)計身高在160~180cm(含160cm,不含180cm)的學生人數(shù),那么在流程圖中的判斷框內(nèi)應填寫的條件是( )
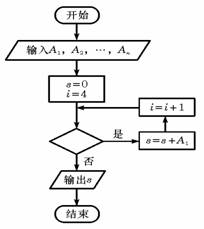 A.i<6 B. i<7 C. i<8 D. i<9
A.i<6 B. i<7 C. i<8 D. i<9
第二部分 非選擇題(共100分)
一、選擇題:本大題每小題5分,滿分50分.
1
2
3
4
5
6
7
8
9
10
C
A
A
C
B
A
B
D
D
B
二、填空題:本大題共5小題,每小題5分,滿分20分,其中14,15題是選做題,考生只能選做一題,,若兩題全都做的,只計算前一題的得分.
11.(2,+∞) 12.量檢測數(shù)學(文科)試題.files/image298.gif) 13. 4 14.
13. 4 14.量檢測數(shù)學(文科)試題.files/image300.gif) 15. 9
15. 9
三、解答題:本大題共6小題,滿分80分.解答須寫出文字說明、證明過程或演算步驟.
16.(本小題滿分12分)
解:(Ⅰ)∵
量檢測數(shù)學(文科)試題.files/image302.gif) , ………………1分
, ………………1分
(Ⅱ)由量檢測數(shù)學(文科)試題.files/image310.gif) 且
且量檢測數(shù)學(文科)試題.files/image312.gif) ,…………………7分
,…………………7分
量檢測數(shù)學(文科)試題.files/image320.gif) 17.(本小題滿分13分)
17.(本小題滿分13分)
證明: (1) ∵ 三棱柱量檢測數(shù)學(文科)試題.files/image205.gif) 為直三棱柱,
為直三棱柱,
∴ 量檢測數(shù)學(文科)試題.files/image322.gif) 平面
平面量檢測數(shù)學(文科)試題.files/image324.gif) , ∴
, ∴量檢測數(shù)學(文科)試題.files/image326.gif) ,
,
∵ 量檢測數(shù)學(文科)試題.files/image207.gif) ,
, 量檢測數(shù)學(文科)試題.files/image209.gif) ,
, 量檢測數(shù)學(文科)試題.files/image211.gif) ,
,
∴ 量檢測數(shù)學(文科)試題.files/image328.gif) ,
,
∴ 量檢測數(shù)學(文科)試題.files/image330.gif) , 又
, 又 量檢測數(shù)學(文科)試題.files/image332.gif) ,
,
∴ 量檢測數(shù)學(文科)試題.files/image334.gif) 平面
平面量檢測數(shù)學(文科)試題.files/image336.gif) ,
,
∴ 量檢測數(shù)學(文科)試題.files/image217.gif) ……………………………………7分
……………………………………7分
(2) 令量檢測數(shù)學(文科)試題.files/image338.gif) 與
與量檢測數(shù)學(文科)試題.files/image340.gif) 的交點為
的交點為量檢測數(shù)學(文科)試題.files/image122.gif) , 連結
, 連結量檢測數(shù)學(文科)試題.files/image343.gif) .
.
∵ 量檢測數(shù)學(文科)試題.files/image182.gif) 是
是量檢測數(shù)學(文科)試題.files/image126.gif) 的中點,
的中點, 量檢測數(shù)學(文科)試題.files/image122.gif) 為
為量檢測數(shù)學(文科)試題.files/image338.gif) 的中點, ∴
的中點, ∴ 量檢測數(shù)學(文科)試題.files/image343.gif) ∥
∥量檢測數(shù)學(文科)試題.files/image219.gif) .
.
又 ∵量檢測數(shù)學(文科)試題.files/image219.gif)
量檢測數(shù)學(文科)試題.files/image347.gif) 平面
平面量檢測數(shù)學(文科)試題.files/image221.gif) ,
, 量檢測數(shù)學(文科)試題.files/image343.gif)
量檢測數(shù)學(文科)試題.files/image350.gif) 平面
平面量檢測數(shù)學(文科)試題.files/image221.gif) ,
,
∴量檢測數(shù)學(文科)試題.files/image219.gif) ∥平面
∥平面量檢測數(shù)學(文科)試題.files/image221.gif) . ………………………13分
. ………………………13分
18.(本小題滿分13分)
解: (1) 由題意得 量檢測數(shù)學(文科)試題.files/image352.gif) , 即
, 即 量檢測數(shù)學(文科)試題.files/image354.gif) ,…………………1分
,…………………1分
當量檢測數(shù)學(文科)試題.files/image356.gif) 時 ,
時 , 量檢測數(shù)學(文科)試題.files/image358.gif) ,…………4分
,…………4分
當量檢測數(shù)學(文科)試題.files/image360.gif) 時,
時, 量檢測數(shù)學(文科)試題.files/image362.gif) , ………………5分
, ………………5分
∴ 量檢測數(shù)學(文科)試題.files/image364.gif) , ……………………6分
, ……………………6分
(2) 由(1)得量檢測數(shù)學(文科)試題.files/image366.gif) ,…………………8分
,…………………8分
∴ 量檢測數(shù)學(文科)試題.files/image368.gif)
量檢測數(shù)學(文科)試題.files/image370.gif) . ……………………11分
. ……………………11分
因此,使得量檢測數(shù)學(文科)試題.files/image372.gif) 成立的
成立的量檢測數(shù)學(文科)試題.files/image108.gif) 必須且只需滿足
必須且只需滿足量檢測數(shù)學(文科)試題.files/image374.gif) , 即
, 即量檢測數(shù)學(文科)試題.files/image376.gif) ,
,
故滿足要求的的最小正整數(shù)量檢測數(shù)學(文科)試題.files/image378.gif) ………………13分
………………13分
19.(本小題滿分14分)
解: (1)設圓量檢測數(shù)學(文科)試題.files/image177.gif) 的圓心為
的圓心為量檢測數(shù)學(文科)試題.files/image380.gif) ,
,
依題意圓的半徑 量檢測數(shù)學(文科)試題.files/image382.gif) ……………… 2分
……………… 2分
∵ 圓量檢測數(shù)學(文科)試題.files/image177.gif) 在
在量檢測數(shù)學(文科)試題.files/image159.gif) 軸上截得的弦
軸上截得的弦量檢測數(shù)學(文科)試題.files/image250.gif) 的長為
的長為量檢測數(shù)學(文科)試題.files/image252.gif) .
.
∴ 量檢測數(shù)學(文科)試題.files/image384.gif)
故 量檢測數(shù)學(文科)試題.files/image386.gif) …………………………
4分
…………………………
4分
∴
量檢測數(shù)學(文科)試題.files/image388.gif)
∴ 圓量檢測數(shù)學(文科)試題.files/image177.gif) 的圓心的軌跡方程為
的圓心的軌跡方程為量檢測數(shù)學(文科)試題.files/image388.gif) ………………… 6分
………………… 6分
(2) ∵
量檢測數(shù)學(文科)試題.files/image254.gif) , ∴
, ∴ 量檢測數(shù)學(文科)試題.files/image390.gif) ……………………… 9分
……………………… 9分
令圓量檢測數(shù)學(文科)試題.files/image177.gif) 的圓心為
的圓心為量檢測數(shù)學(文科)試題.files/image392.gif) , 則有
, 則有量檢測數(shù)學(文科)試題.files/image394.gif) (
(量檢測數(shù)學(文科)試題.files/image396.gif) ) ,…………… 10分
) ,…………… 10分
又
∵ 量檢測數(shù)學(文科)試題.files/image398.gif) …………………… 11分
…………………… 11分
∴ 量檢測數(shù)學(文科)試題.files/image400.gif) ……………………… 12分
……………………… 12分
∴ 量檢測數(shù)學(文科)試題.files/image402.gif) ………………………
13分
………………………
13分
∴ 圓量檢測數(shù)學(文科)試題.files/image177.gif) 的方程為
的方程為 量檢測數(shù)學(文科)試題.files/image404.gif) …………………… 14分
…………………… 14分
21.(本小題滿分14分)
解:(Ⅰ)由已知量檢測數(shù)學(文科)試題.files/image406.gif)
解得量檢測數(shù)學(文科)試題.files/image289.gif) ,
,量檢測數(shù)學(文科)試題.files/image409.gif) ,
…………………2分
,
…………………2分
∴ 量檢測數(shù)學(文科)試題.files/image411.gif) , ∴
, ∴ 量檢測數(shù)學(文科)試題.files/image413.gif) …………4分
…………4分
∴ 量檢測數(shù)學(文科)試題.files/image415.gif) . ……………………5分
. ……………………5分
(Ⅱ)在(Ⅰ)條件下,量檢測數(shù)學(文科)試題.files/image268.gif) 在區(qū)間
在區(qū)間量檢測數(shù)學(文科)試題.files/image270.gif) 恒成立,即
恒成立,即量檢測數(shù)學(文科)試題.files/image417.gif) 在區(qū)間
在區(qū)間量檢測數(shù)學(文科)試題.files/image270.gif) 恒成立,
恒成立,
從而量檢測數(shù)學(文科)試題.files/image419.gif) 在區(qū)間
在區(qū)間量檢測數(shù)學(文科)試題.files/image270.gif) 上恒成立,…………………8分
上恒成立,…………………8分
令函數(shù)量檢測數(shù)學(文科)試題.files/image422.gif) ,
,
則函數(shù)量檢測數(shù)學(文科)試題.files/image422.gif) 在區(qū)間
在區(qū)間量檢測數(shù)學(文科)試題.files/image270.gif) 上是減函數(shù),且其最小值
上是減函數(shù),且其最小值量檢測數(shù)學(文科)試題.files/image425.gif) ,
,
∴ 量檢測數(shù)學(文科)試題.files/image272.gif) 的取值范圍為
的取值范圍為量檢測數(shù)學(文科)試題.files/image428.gif) …………………………10分
…………………………10分
(Ⅲ)由量檢測數(shù)學(文科)試題.files/image276.gif) ,得
,得量檢測數(shù)學(文科)試題.files/image431.gif) ,
,
∵
量檢測數(shù)學(文科)試題.files/image433.gif) ∴
∴量檢測數(shù)學(文科)試題.files/image435.gif) ,………………11分
,………………11分
設方程量檢測數(shù)學(文科)試題.files/image437.gif) 的兩根為
的兩根為量檢測數(shù)學(文科)試題.files/image439.gif) ,則
,則量檢測數(shù)學(文科)試題.files/image441.gif) ,
,量檢測數(shù)學(文科)試題.files/image443.gif) ,
,
∴量檢測數(shù)學(文科)試題.files/image445.gif) ,
,
∵
量檢測數(shù)學(文科)試題.files/image281.gif) , ∴
, ∴ 量檢測數(shù)學(文科)試題.files/image447.gif) , ∴
, ∴量檢測數(shù)學(文科)試題.files/image449.gif) ,
,
∵
量檢測數(shù)學(文科)試題.files/image433.gif) 且
且量檢測數(shù)學(文科)試題.files/image452.gif) , ∴
, ∴ 量檢測數(shù)學(文科)試題.files/image454.gif) ,
,
∴
量檢測數(shù)學(文科)試題.files/image456.gif) ……………14分
……………14分
21.(本小題滿分14分)
解: (Ⅰ)解:當量檢測數(shù)學(文科)試題.files/image289.gif) 時,
時,量檢測數(shù)學(文科)試題.files/image459.gif) ,
,量檢測數(shù)學(文科)試題.files/image461.gif) ,……………1分
,……………1分
又量檢測數(shù)學(文科)試題.files/image463.gif) ,則
,則量檢測數(shù)學(文科)試題.files/image465.gif) .…………………3分
.…………………3分
所以,曲線量檢測數(shù)學(文科)試題.files/image291.gif) 在點
在點量檢測數(shù)學(文科)試題.files/image293.gif) 處的切線方程為
處的切線方程為量檢測數(shù)學(文科)試題.files/image469.gif) ,
,
即量檢測數(shù)學(文科)試題.files/image471.gif) .……………4分
.……………4分
(Ⅱ)解:量檢測數(shù)學(文科)試題.files/image473.gif) .…………6分
.…………6分
由于量檢測數(shù)學(文科)試題.files/image295.gif) ,以下分兩種情況討論.
,以下分兩種情況討論.
(1)當量檢測數(shù)學(文科)試題.files/image433.gif) 時,令
時,令量檢測數(shù)學(文科)試題.files/image477.gif) ,得到
,得到量檢測數(shù)學(文科)試題.files/image479.gif) ,
,量檢測數(shù)學(文科)試題.files/image481.gif) ,
,
當量檢測數(shù)學(文科)試題.files/image159.gif) 變化時,
變化時,量檢測數(shù)學(文科)試題.files/image484.gif) 的變化情況如下表:
的變化情況如下表:
量檢測數(shù)學(文科)試題.files/image159.gif)
量檢測數(shù)學(文科)試題.files/image487.gif)
量檢測數(shù)學(文科)試題.files/image489.gif)
量檢測數(shù)學(文科)試題.files/image491.gif)
量檢測數(shù)學(文科)試題.files/image063.gif)
量檢測數(shù)學(文科)試題.files/image494.gif)
量檢測數(shù)學(文科)試題.files/image496.gif)
量檢測數(shù)學(文科)試題.files/image498.gif)
0
量檢測數(shù)學(文科)試題.files/image500.gif)
0
量檢測數(shù)學(文科)試題.files/image498.gif)
量檢測數(shù)學(文科)試題.files/image260.gif)
量檢測數(shù)學(文科)試題.files/image504.gif)
極小值
量檢測數(shù)學(文科)試題.files/image506.gif)
極大值
量檢測數(shù)學(文科)試題.files/image504.gif)
所以量檢測數(shù)學(文科)試題.files/image260.gif) 在區(qū)間
在區(qū)間量檢測數(shù)學(文科)試題.files/image509.gif) ,
,量檢測數(shù)學(文科)試題.files/image511.gif) 內(nèi)為減函數(shù),在區(qū)間
內(nèi)為減函數(shù),在區(qū)間量檢測數(shù)學(文科)試題.files/image513.gif) 內(nèi)為增函數(shù)
內(nèi)為增函數(shù)
故函數(shù)量檢測數(shù)學(文科)試題.files/image260.gif) 在點
在點量檢測數(shù)學(文科)試題.files/image479.gif) 處取得極小值
處取得極小值量檢測數(shù)學(文科)試題.files/image517.gif) ,且
,且量檢測數(shù)學(文科)試題.files/image519.gif) ,
,
函數(shù)量檢測數(shù)學(文科)試題.files/image260.gif) 在點
在點量檢測數(shù)學(文科)試題.files/image481.gif) 處取得極大值
處取得極大值量檢測數(shù)學(文科)試題.files/image523.gif) ,且
,且量檢測數(shù)學(文科)試題.files/image525.gif) .…………………10分
.…………………10分
(2)當量檢測數(shù)學(文科)試題.files/image527.gif) 時,令
時,令量檢測數(shù)學(文科)試題.files/image477.gif) ,得到
,得到量檢測數(shù)學(文科)試題.files/image530.gif) ,
,
當量檢測數(shù)學(文科)試題.files/image159.gif) 變化時,
變化時,量檢測數(shù)學(文科)試題.files/image484.gif) 的變化情況如下表:
的變化情況如下表:
量檢測數(shù)學(文科)試題.files/image159.gif)
量檢測數(shù)學(文科)試題.files/image533.gif)
量檢測數(shù)學(文科)試題.files/image063.gif)
量檢測數(shù)學(文科)試題.files/image536.gif)
量檢測數(shù)學(文科)試題.files/image489.gif)
量檢測數(shù)學(文科)試題.files/image539.gif)
量檢測數(shù)學(文科)試題.files/image496.gif)
量檢測數(shù)學(文科)試題.files/image500.gif)
0
量檢測數(shù)學(文科)試題.files/image498.gif)
0
量檢測數(shù)學(文科)試題.files/image500.gif)
量檢測數(shù)學(文科)試題.files/image260.gif)
量檢測數(shù)學(文科)試題.files/image506.gif)
極大值
量檢測數(shù)學(文科)試題.files/image504.gif)
極小值
量檢測數(shù)學(文科)試題.files/image506.gif)
所以量檢測數(shù)學(文科)試題.files/image260.gif) 在區(qū)間
在區(qū)間量檢測數(shù)學(文科)試題.files/image542.gif) ,
,量檢測數(shù)學(文科)試題.files/image543.gif) 內(nèi)為增函數(shù),在區(qū)間
內(nèi)為增函數(shù),在區(qū)間量檢測數(shù)學(文科)試題.files/image544.gif) 內(nèi)為減函數(shù).
內(nèi)為減函數(shù).
函數(shù)量檢測數(shù)學(文科)試題.files/image260.gif) 在
在量檢測數(shù)學(文科)試題.files/image546.gif) 處取得極大值
處取得極大值量檢測數(shù)學(文科)試題.files/image523.gif) ,且
,且量檢測數(shù)學(文科)試題.files/image525.gif) .
.
函數(shù)量檢測數(shù)學(文科)試題.files/image260.gif) 在
在量檢測數(shù)學(文科)試題.files/image550.gif) 處取得極小值
處取得極小值量檢測數(shù)學(文科)試題.files/image517.gif) ,且
,且量檢測數(shù)學(文科)試題.files/image519.gif) .………………14分
.………………14分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com