題目列表(包括答案和解析)
已知數(shù)列
的前
項和為
，且
(
N*),其中
．
(Ⅰ) 求的通項公式；
(Ⅱ) 設(shè)
(
N*).
①證明： 
；
② 求證：
.
【解析】本試題主要考查了數(shù)列的通項公式的求解和運用。運用
關(guān)系式，表示通項公式，然后得到第一問，第二問中利用放縮法得到
，②由于
，
所以
利用放縮法，從此得到結(jié)論。
解：(Ⅰ)當(dāng)
時，由
得
. ……2分
若存在
由
得
，
從而有
，與矛盾，所以
.
從而由得
得
. ……6分
(Ⅱ)①證明：
證法一：∵
∴
∴
∴
.…………10分
證法二：
，下同證法一.
……10分
證法三：（利用對偶式）設(shè)
，
，
則
.又
，也即
，所以
，也即
，又因為
，所以
.即
………10分
證法四：（數(shù)學(xué)歸納法）①當(dāng)
時, 
,命題成立;
②假設(shè)
時,命題成立,即
,
則當(dāng)
時,
即
即
故當(dāng)時，命題成立.
綜上可知，對一切非零自然數(shù)，不等式②成立. ………………10分
②由于，
所以，
從而
.
也即
已知遞增等差數(shù)列
滿足：
，且
成等比數(shù)列．
（1）求數(shù)列的通項公式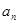
；
（2）若不等式
對任意
恒成立，試猜想出實數(shù)
的最小值，并證明．
【解析】本試題主要考查了數(shù)列的通項公式的運用以及數(shù)列求和的運用。第一問中，利用設(shè)數(shù)列公差為
，
由題意可知
，即
，解得d，得到通項公式，第二問中，不等式等價于
，利用當(dāng)
時，
；當(dāng)
時，
；而
，所以猜想，的最小值為
然后加以證明即可。
解：（1）設(shè)數(shù)列公差為，由題意可知，即，
解得
或
（舍去）． …………3分
所以，
． …………6分
（2）不等式等價于，
當(dāng)時，；當(dāng)時，；
而，所以猜想，的最小值為． …………8分
下證不等式
對任意恒成立．
方法一：數(shù)學(xué)歸納法．
當(dāng)時，
，成立．
假設(shè)當(dāng)
時，不等式
成立，
當(dāng)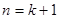
時，
，
…………10分
只要證 
，只要證 
，
只要證 
，只要證 
，
只要證 
，顯然成立．所以，對任意，不等式恒成立．…14分
方法二：單調(diào)性證明．
要證
只要證 
，
設(shè)數(shù)列
的通項公式
， …………10分
， …………12分
所以對
，都有
，可知數(shù)列為單調(diào)遞減數(shù)列．
而
，所以
恒成立，
故的最小值為．
中國籃球職業(yè)聯(lián)賽某賽季的總決賽在某兩隊之間角逐，采用七局四勝制，即若有一隊先勝四場，則此隊獲勝，比賽就此結(jié)束．因兩隊實力相當(dāng)，每場比賽獲勝的可能性相等．據(jù)以往資料統(tǒng)計，第一場比賽組織者可獲門票收入30萬元，以后每場比賽門票收入都比上一場增加10萬元，當(dāng)兩隊決出勝負(fù)后．問：
(1)組織者在此次決賽中要獲得門票收入為180萬元須比賽多少場？
(2)組織者在此次決賽中獲得門票收入不少于330萬元的概率為多少？
分析：本題是一個概率與數(shù)列的綜合試題，可以首先求出收入的通項公式，從而得出比賽的場數(shù)，再確定其概率．
2007年12月29日第十屆全國人大常委會第三十一次會議表決通過了《關(guān)于修改〈中華人民共和國個人所得稅法〉的決定》，將個人所得稅工資、薪金所得減除費用標(biāo)準(zhǔn)由每月1600元提高到每月2000元，同時明確自2008年3月1日起施行．即公民全月工資，薪金所得不超過2000元的部分不必納稅，超過2000元的部分應(yīng)納稅，此項稅款按下表分段累進計算：
注明：上表中“全月應(yīng)納稅所得額”是從月工資、薪金收入中減去2000元后的余額．例如某人月工資、薪金收入為3000元，減去2000元，應(yīng)納稅所得額為1000元，由稅率表知其中500元稅率為5％，另外500元的稅率為10％，所以此人應(yīng)納個人所得稅為500×5％＋500×10％＝75元．
(1)請寫出月工資，薪金的個人所得稅y關(guān)于工資，薪金收入x(0＜x≤5000)的函數(shù)表達式；
(2)某高中數(shù)學(xué)教師在2008年10月份繳納的個人所得稅是40元，試求他這個月的工資，薪金收入是多少？
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com