
題目列表(包括答案和解析)
下列命題中正確的是 ( )
A.若p∨q為真命題,則p∧q為真命題
B.“x=5”是“x2-4x-5=0”的充分不必要條件
C.命題“若x<-1,則x2-2x-3>0”的否定為:“若x≥-1,則x2-2x-3≤0”
D.已知命題p:∃x∈R,x2+x-1<0,則綈p:∃x∈R,x2+x-1≥0
已知 是公差為d的等差數列,
是公差為d的等差數列, 是公比為q的等比數列
是公比為q的等比數列
(Ⅰ)若  ,是否存在
,是否存在 ,有
,有 ?請說明理由;
?請說明理由;
(Ⅱ)若 (a、q為常數,且aq
(a、q為常數,且aq 0)對任意m存在k,有
0)對任意m存在k,有 ,試求a、q滿足的充要條件;
,試求a、q滿足的充要條件;
(Ⅲ)若 試確定所有的p,使數列
試確定所有的p,使數列 中存在某個連續p項的和式數列中
中存在某個連續p項的和式數列中 的一項,請證明.
的一項,請證明.
【解析】第一問中,由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 為整數
為整數 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)中當 時,則
時,則
 即
即 ,其中
,其中 是大于等于
是大于等于 的整數
的整數
反之當 時,其中
時,其中 是大于等于
是大于等于 的整數,則
的整數,則 ,
,
顯然 ,其中
,其中

 、
、 滿足的充要條件是
滿足的充要條件是 ,其中
,其中 是大于等于
是大于等于 的整數
的整數
(3)中設 當
當 為偶數時,
為偶數時, 式左邊為偶數,右邊為奇數,
式左邊為偶數,右邊為奇數,
當 為偶數時,
為偶數時, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
當 時,符合題意。當
時,符合題意。當 ,
, 為奇數時,
為奇數時,
結合二項式定理得到結論。
解(1)由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 為整數
為整數 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)當 時,則
時,則
 即
即 ,其中
,其中 是大于等于
是大于等于 的整數反之當
的整數反之當 時,其中
時,其中 是大于等于
是大于等于 的整數,則
的整數,則 ,
,
顯然 ,其中
,其中

 、
、 滿足的充要條件是
滿足的充要條件是 ,其中
,其中 是大于等于
是大于等于 的整數
的整數
(3)設 當
當 為偶數時,
為偶數時, 式左邊為偶數,右邊為奇數,
式左邊為偶數,右邊為奇數,
當 為偶數時,
為偶數時, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
當 時,符合題意。當
時,符合題意。當 ,
, 為奇數時,
為奇數時,

 由
由 ,得
,得

 當
當 為奇數時,此時,一定有
為奇數時,此時,一定有 和
和 使上式一定成立。
使上式一定成立。 當
當 為奇數時,命題都成立
為奇數時,命題都成立
已知 ,
, 是橢圓
是橢圓
 左右焦點,它的離心率
左右焦點,它的離心率 ,且被直線
,且被直線 所截得的線段的中點的橫坐標為
所截得的線段的中點的橫坐標為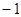
(Ⅰ)求橢圓的標準方程;
(Ⅱ)設 是其橢圓上的任意一點,當
是其橢圓上的任意一點,當 為鈍角時,求
為鈍角時,求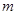 的取值范圍。
的取值范圍。
【解析】解:因為第一問中,利用橢圓的性質由 得
得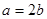 所以橢圓方程可設為:
所以橢圓方程可設為: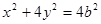 ,然后利用
,然后利用
得 得
得


 橢圓方程為
橢圓方程為
第二問中,當 為鈍角時,
為鈍角時, ,
得
,
得
所以 得
得
解:(Ⅰ)由 得
得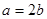 所以橢圓方程可設為:
所以橢圓方程可設為: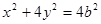
 3分
3分
得 得
得


 橢圓方程為
橢圓方程為 3分
3分
(Ⅱ)當 為鈍角時,
為鈍角時, ,
得
,
得 3分
3分
所以 得
得
設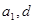 為實數,首項為
為實數,首項為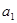 ,公差為
,公差為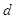 的等差數列
的等差數列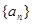 的前n項和為
的前n項和為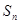 ,滿足
,滿足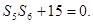
(1)若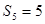 ,求
,求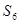 及
及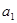 ;
;
(2)求d的取值范圍.
【解析】本試題主要考查了數列的求和的運用以及通項公式的運用。第一問中,利用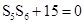 和已知的
和已知的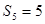 ,得到結論
,得到結論
第二問中,利用首項和公差表示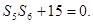 ,則方程是一個有解的方程,因此判別式大于等于零,因此得到d的范圍。
,則方程是一個有解的方程,因此判別式大于等于零,因此得到d的范圍。
解:(1)因為設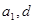 為實數,首項為
為實數,首項為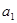 ,公差為
,公差為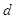 的等差數列
的等差數列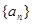 的前n項和為
的前n項和為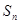 ,滿足
,滿足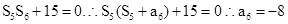
所以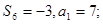
(2)因為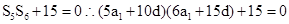
得到關于首項的一個二次方程,則方程必定有解,結合判別式求解得到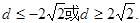
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com