无码精品日韩专区第一页,亚洲国产一区二区我是潘金莲,大香蕉在线视频观看地址

(2) 的最大值和最小值. (三) 【查看更多】

題目列表(包括答案和解析)

(本小題滿分12分)
在某校組織的一次籃球定點(diǎn)投籃訓(xùn)練中，規(guī)定每人最多投3次；在A處每投進(jìn)一球得3分，在B處每投進(jìn)一球得2分；如果前兩次得分之和超過(guò)3分即停止投籃，否則投第三次，某同學(xué)在A處的命中率q

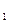為0.25，在B處的命中率為q

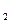，該同學(xué)選擇先在A處投一球，以后都在B處投，用

表示該同學(xué)投籃訓(xùn)練結(jié)束后所得的總分，其分布列為

	0	2	3	4	5
p	0.03	P₁	P₂	P₃	P₄

（1）求q

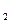的值；
（2）求隨機(jī)變量

的數(shù)學(xué)期望E

;
（3）試比較該同學(xué)選擇都在B處投籃得分超過(guò)3分與選擇上述方式投籃得分超過(guò)3分的概率的大小。

查看答案和解析>>

（本小題滿分10分）

在某學(xué)校組織的一次藍(lán)球定點(diǎn)投藍(lán)訓(xùn)練中，規(guī)定每人最多投3次；在A處每投進(jìn)一球得3分，在B處每投進(jìn)一球得2分；如果前兩次得分之和超過(guò)3分即停止投籃，否則投三次。某同學(xué)在A處的命中率為0.25，在B處的命中率為.該同學(xué)選擇先在A處投一球，以后都在B處投，用表示該同學(xué)投籃訓(xùn)練結(jié)束后所得的總分，其分布列為

	0	2	3	4	5
	0．03

求的值；

求隨機(jī)變量的數(shù)學(xué)期量；

試比較該同學(xué)選擇都在B處投籃得分超過(guò)3分與選擇上述方式投籃得分超過(guò)3分的概率的大小。

查看答案和解析>>

設(shè)函數(shù)。

（Ⅰ）求函數(shù)的最大值和最小正周期；w.w.w.k.s.5.u.c.o.m

（Ⅱ）設(shè)A，B，C為的三個(gè)內(nèi)角，若，且C為銳角，求

查看答案和解析>>

設(shè)函數(shù).
（1）求函數(shù)f(x)的最大值和最小正周期。
（2）設(shè)A、B、C為⊿ABC的三個(gè)內(nèi)角，若，，且C為銳角，求.

查看答案和解析>>

在某校組織的一次籃球定點(diǎn)投籃訓(xùn)練中，規(guī)定每人最多投3次；在A處每投進(jìn)一球得3分，在B處每投進(jìn)一球得2分；如果前兩次得分之和超過(guò)3分即停止投籃，否則投第三次，某同學(xué)在A處的命中率q為0.25，在B處的命中率為q，該同學(xué)選擇先在A處投一球，以后都在B處投，用表示該同學(xué)投籃訓(xùn)練結(jié)束后所得的總分，其分布列為

	0	2	3	4	5
w.w.w.k.s.5.u.c.o.m p	0.03	P₁	P₂	P₃	P₄

（1）求q的值；w.w.w.k.s.5.u.c.o.m

（2）求隨機(jī)變量的數(shù)學(xué)期望E;

（3）試比較該同學(xué)選擇都在B處投籃得分超過(guò)3分與選擇上述方式投籃得分超過(guò)3分的概率的大小。

查看答案和解析>>

天津精通高考復(fù)讀學(xué)校數(shù)學(xué)教研組組長(zhǎng) 么世濤

一、選擇題：1-4， BBBB ；5-8，DABD。

提示：1.

3.用代替得

4．

5.,或

7．略

8．

二、填空題：9.60； 10. 15：10：20 ； 11.； 12.；

13.0.74 ； 14. ①、；②、圓；③.

提示： 9.

10．，，

11．，

12．，，，

，

13．

14．略

三、解答題

15. 解：(1).

(2)設(shè)抽取件產(chǎn)品作檢驗(yàn)，則，

，得：，即

故至少應(yīng)抽取8件產(chǎn)品才能滿足題意.

16. 解：由題意得，，原式可化為,

而

故原式=.

17. 解：(1)顯然，連接，∵，，

∴.由已知，∴，.

∵∽，，

∴ 即 .

∴.

(2)

當(dāng)且僅當(dāng)時(shí)，等號(hào)成立.此時(shí)，即為的中點(diǎn).于是由，知平面，是其交線，則過(guò)作

。

∴就是與平面所成的角.由已知得，，

∴， , .

(3) 設(shè)三棱錐的內(nèi)切球半徑為，則

∵，，，，，

∴.

18. 解： (1) ，

(2) ∵ ，

∴當(dāng)時(shí)，

∴當(dāng)時(shí)，，

∵,,,.

∴ 的最大值為或中的最大者．

∵

∴ 當(dāng)時(shí)，有最大值為．

19.(1)解：∵函數(shù)的圖象過(guò)原點(diǎn)，

∴即，

∴.

又函數(shù)的圖象關(guān)于點(diǎn)成中心對(duì)稱，

∴， .

(2)解：由題意有即，

即，即.

∴數(shù)列{}是以1為首項(xiàng)，1為公差的等差數(shù)列.

∴，即. ∴.

∴ ，，，.

(3)證明：當(dāng)時(shí)，

故

20. (1)解：∵，又，

∴. 又∵

，且

∴ .

(2)解：由，，猜想

(3)證明：用數(shù)學(xué)歸納法證明：

①當(dāng)時(shí)，，猜想正確；

②假設(shè)時(shí)，猜想正確，即

1°若為正奇數(shù)，則為正偶數(shù)，為正整數(shù)，

2°若為正偶數(shù)，則為正整數(shù)，

，又，且

所以

即當(dāng)時(shí)，猜想也正確

由①，②可知，成立.

（二）

一、1-4，AABB,5-8,CDCB；

提示： 1. 即

2．即

3．即，也就是，

4．先確定是哪兩個(gè)人的編號(hào)與座位號(hào)一致，有種情況，如編號(hào)為1的人坐1號(hào)座位，且編號(hào)為2的人坐2號(hào)座位有以下情形：

人的編號(hào)

座位號(hào)

人的編號(hào)

座位號(hào)

所以，符合條件的共有10×2=20種。

5．，又，所以

又，且，所以

6．略

7．略

8．密文shxc中的s對(duì)應(yīng)的數(shù)字為19，按照變換公式：

，原文對(duì)應(yīng)的數(shù)字是12，對(duì)應(yīng)的字母是；

密文shxc中的h對(duì)應(yīng)的數(shù)字為8，按照變換公式：

，原文對(duì)應(yīng)的數(shù)字是15，對(duì)應(yīng)的字母是；

二、9．； 10.2；11.-48； 12. ； 13、5； 14、①3，②，③

提示：

9. ，，

10. 數(shù)列是首相為，公差為的等差數(shù)列，于是

又，所以

11. 特殊值法。取通徑，則，，

。

12．因，，所以同解于

又

所以。

13．略。

14、（1）如圖：∵

∴∠1＝∠2＝∠3＝∠P＋∠PFD

＝∠FEO＋∠EFO

∴∠FEO＝∠P，可證△OEF∽△DPF

即有，又根據(jù)相交弦定理DF?EF＝BF?AF

可推出，從而

∴PF＝3

（2） ∵PFQF，　　∴　　∴

(3)略。

三、15．解：(1) 依題知，得

文本框: 子曰：三人行，必有我?guī)熝桑簱衿渖普叨鴱闹洳簧普叨闹＞▋?nèi)部學(xué)員使用么老師答疑電話
13702071025 又所以

(2) 由(1)得

∴

故的值域?yàn)?sub>。

16．解：設(shè)飛機(jī)A能安全飛行的概率為，飛機(jī)B能安全飛行的概率為，則

又所以

當(dāng)時(shí)，，，；

故當(dāng)時(shí)，飛機(jī)A安全；當(dāng)時(shí)，飛機(jī)A與飛機(jī)B一樣安全；當(dāng)時(shí)，飛機(jī)B安全。

17．(1) 證明：以D為坐標(biāo)原點(diǎn)，DA所在的直線x

軸，建立空間直角坐標(biāo)系如圖。

設(shè),則

，，，

，

又，所以

即，也就是

又，所以，即。

(2)解：方法1、找出二面角，再計(jì)算。

方法2、由(1)得：(當(dāng)且僅當(dāng)取等號(hào))

即分別為的中點(diǎn)，于是，。

又，所以，

設(shè)是平面的一個(gè)法向量，則

即也就是

取

易知是平面的一個(gè)法向量，

18．(1) 證明：依題知得：

整理，得

又所以即

故數(shù)列是等差數(shù)列。

(2) 由(1)得即 ()

又所以

故

19．解：(1) 依題知得

欲使函數(shù)在是增函數(shù)，僅須或

同步練習(xí)冊(cè)答案

國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表

湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)

違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
版權(quán)聲明：本站所有文章，圖片來(lái)源于網(wǎng)絡(luò)，著作權(quán)及版權(quán)歸原作者所有，轉(zhuǎn)載無(wú)意侵犯版權(quán)，如有侵權(quán)，請(qǐng)作者速來(lái)函告知，我們將盡快處理，聯(lián)系qq：3310059649。
ICP備案序號(hào): 滬ICP備07509807號(hào)-10 鄂公網(wǎng)安備42018502000812號(hào)

国产日韩欧美一线二线,美女好全身无遮掩免费网战,亚洲欧美另类卡通乱,日韩av日日夜夜澡,女生抽打女生大骚逼,国产精品99久久…,五月婷婷六月丁香亚洲天堂,中文无码精品一区二区三,日本日p视频免费在线观看

練習(xí)冊(cè)

高中

初中

小學(xué)