
題目列表(包括答案和解析)
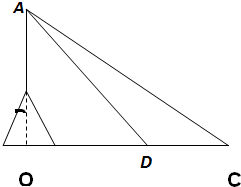 如圖,某海域內(nèi)的島嶼上有一直立信號塔AB,設AB延長線與海平面交于點O.測量船在點O的正東方向點C處,測得塔頂A的仰角為30°,然后測量船沿CO方向航行至D處,當CD=100(
如圖,某海域內(nèi)的島嶼上有一直立信號塔AB,設AB延長線與海平面交于點O.測量船在點O的正東方向點C處,測得塔頂A的仰角為30°,然后測量船沿CO方向航行至D處,當CD=100(| 3 |
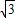 -1)米時,測得塔頂A的仰角為45°.
-1)米時,測得塔頂A的仰角為45°.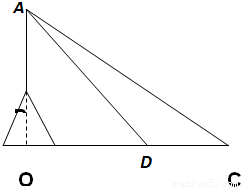
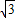 -1)米時,測得塔頂A的仰角為45°.
-1)米時,測得塔頂A的仰角為45°.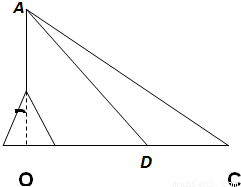
已知拋物線![]() (
(![]() 為非零常數(shù))的焦點為
為非零常數(shù))的焦點為![]() ,點
,點![]() 為拋物線
為拋物線![]() 上一個動點,過點
上一個動點,過點![]() 且與拋物線
且與拋物線![]() 相切的直線記為
相切的直線記為![]() .
.
(1)求![]() 的坐標;
的坐標;
(2)當點![]() 在何處時,點
在何處時,點![]() 到直線
到直線![]() 的距離最小?
的距離最小?
已知拋物線![]() (
(![]() 為非零常數(shù))的焦點為
為非零常數(shù))的焦點為![]() ,點
,點![]() 為拋物線
為拋物線![]() 上一個動點,過點
上一個動點,過點![]() 且與拋物線
且與拋物線![]() 相切的直線記為
相切的直線記為![]() .
.
(1)求![]() 的坐標;
的坐標;
(2)當點![]() 在何處時,點
在何處時,點![]() 到直線
到直線![]() 的距離最小?
的距離最小?
一、選擇題:本大題共8小題,每小題5分,滿分40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.D 2.B 3.D 4.A 5.C 6.D 7.C 8.A
二、填空題:本大題共7小題,每小題5分,滿分30分.其中13~15題是選做題,考生只能選做二題,三題全答的,只計算前兩題得分.
9.學試卷_理.files/image258.gif) 10.
10.學試卷_理.files/image260.gif) (或
(或學試卷_理.files/image262.gif) ) 11.
) 11.學試卷_理.files/image264.gif)
12.學試卷_理.files/image036.gif) 13.
13.學試卷_理.files/image024.gif) 14.
14.學試卷_理.files/image268.gif)
15.學試卷_理.files/image270.gif)
三、解答題:本大題共6小題,滿分80分.解答須寫出文字說明、證明過程和演算步驟.
16.(本小題滿分12分)
解:學試卷_理.files/image272.gif) ,……………………………………………… 3分
,……………………………………………… 3分
學試卷_理.files/image274.gif) ,……………………… 3分
,……………………… 3分
(1)學試卷_理.files/image276.gif) ;……………………………………………………. 2分
;……………………………………………………. 2分
(2)因為學試卷_理.files/image162.gif) 的解集為
的解集為學試卷_理.files/image278.gif) ,
,
所以學試卷_理.files/image280.gif) 為
為學試卷_理.files/image282.gif) 的兩根,……………………………………… 2分
的兩根,……………………………………… 2分
故學試卷_理.files/image284.gif) ,所以
,所以學試卷_理.files/image286.gif) ,
,學試卷_理.files/image288.gif) .……………………………………. 2分
.……………………………………. 2分
17.(本小題滿分12分)
解: 學試卷_理.files/image290.gif) ………………………………………… 2分
………………………………………… 2分
學試卷_理.files/image292.gif)
學試卷_理.files/image294.gif) ………………………………………… 2分
………………………………………… 2分
學試卷_理.files/image296.gif) ……………………………………………………. 2分
……………………………………………………. 2分
(1)學試卷_理.files/image069.gif) 的最大值為
的最大值為學試卷_理.files/image024.gif) 、最小值為
、最小值為學試卷_理.files/image300.gif) ;……………………………………………… 2分
;……………………………………………… 2分
(2)學試卷_理.files/image069.gif) 單調(diào)增,故
單調(diào)增,故學試卷_理.files/image302.gif) ,…………………………… 2分
,…………………………… 2分
即學試卷_理.files/image304.gif) ,
,
從而學試卷_理.files/image069.gif) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為學試卷_理.files/image306.gif) .…………………… 2分
.…………………… 2分
18.(本小題滿分14分)
(1)證明:學試卷_理.files/image177.gif) 底面
底面學試卷_理.files/image179.gif) ,
,學試卷_理.files/image308.gif)
又學試卷_理.files/image310.gif) ,
,學試卷_理.files/image312.gif) ,故
,故學試卷_理.files/image314.gif) 面
面學試卷_理.files/image316.gif)
學試卷_理.files/image318.gif) 面
面學試卷_理.files/image316.gif) ,故
,故學試卷_理.files/image193.gif) ………………………………………………… 4分
………………………………………………… 4分
(2)證明:學試卷_理.files/image187.gif) ,
,學試卷_理.files/image185.gif) ,故
,故學試卷_理.files/image321.gif)
學試卷_理.files/image189.gif) 是
是學試卷_理.files/image191.gif) 的中點,故
的中點,故學試卷_理.files/image323.gif)
由(1)知學試卷_理.files/image193.gif) ,從而
,從而學試卷_理.files/image325.gif) 面
面學試卷_理.files/image327.gif) ,故
,故學試卷_理.files/image329.gif)
易知學試卷_理.files/image331.gif) ,故
,故學試卷_理.files/image195.gif) 面
面學試卷_理.files/image197.gif) ……………………………………………… 5分
……………………………………………… 5分
(3)過點學試卷_理.files/image333.gif) 作
作學試卷_理.files/image335.gif) ,垂足為
,垂足為學試卷_理.files/image204.gif) ,連結(jié)
,連結(jié)學試卷_理.files/image338.gif) .
.
由(2)知,學試卷_理.files/image325.gif) 面
面學試卷_理.files/image327.gif) ,故
,故學試卷_理.files/image340.gif) 是二面角
是二面角學試卷_理.files/image199.gif) 的一個平面角.
的一個平面角.
設學試卷_理.files/image342.gif) ,則
,則學試卷_理.files/image344.gif) ,
,學試卷_理.files/image346.gif) ,
,學試卷_理.files/image348.gif)
從而學試卷_理.files/image350.gif) ,故
,故學試卷_理.files/image352.gif) .……………… 5分
.……………… 5分
說明:如學生用向量法解題,則建立坐標系給2分,寫出相關點的坐標給2分,第(1)問正確給2分,第(2)問正確給4分,第(3)問正確給4分。
19.(本小題滿分14分)
解:(1)拋物線方程為學試卷_理.files/image354.gif) ……………………………………………………… 2分
……………………………………………………… 2分
故焦點學試卷_理.files/image204.gif) 的坐標為
的坐標為學試卷_理.files/image357.gif) ………………………………………………………… 2分
………………………………………………………… 2分
(2)設學試卷_理.files/image359.gif)
學試卷_理.files/image361.gif)
學試卷_理.files/image363.gif)
學試卷_理.files/image365.gif)
學試卷_理.files/image367.gif)
學試卷_理.files/image369.gif)
學試卷_理.files/image371.gif)
學試卷_理.files/image373.gif)
20.(本小題滿分14分)
解:(1)當學試卷_理.files/image375.gif) 時,
時,學試卷_理.files/image377.gif) ,
,
學試卷_理.files/image379.gif)
當學試卷_理.files/image381.gif) 時,
時,學試卷_理.files/image383.gif)
學試卷_理.files/image385.gif)
學試卷_理.files/image387.gif)
學試卷_理.files/image389.gif)
所以學試卷_理.files/image391.gif)
學試卷_理.files/image393.gif) ;…………………… 4分
;…………………… 4分
(2)因為學試卷_理.files/image395.gif) ,
,
所以學試卷_理.files/image397.gif)
學試卷_理.files/image399.gif)
當學試卷_理.files/image401.gif) 時,
時,學試卷_理.files/image403.gif) ,
,學試卷_理.files/image405.gif)
當學試卷_理.files/image407.gif) 時,
時,學試卷_理.files/image409.gif) ,
,學試卷_理.files/image411.gif)
所以當學試卷_理.files/image230.gif) ,
,學試卷_理.files/image232.gif) 且
且學試卷_理.files/image234.gif) 時,
時,學試卷_理.files/image413.gif) ,即
,即學試卷_理.files/image415.gif) ;………… 5分
;………… 5分
(3)因為學試卷_理.files/image381.gif) ,
,學試卷_理.files/image418.gif) ,所以
,所以學試卷_理.files/image395.gif) ,
,
因為學試卷_理.files/image421.gif) 為等比數(shù)列,則
為等比數(shù)列,則學試卷_理.files/image423.gif) 或
或學試卷_理.files/image425.gif) ,
,
所以學試卷_理.files/image427.gif) 或
或學試卷_理.files/image429.gif) (舍去),所以
(舍去),所以學試卷_理.files/image427.gif) .………………………… 5分
.………………………… 5分
21.(本小題滿分14分)
解:(1)由題意知,學試卷_理.files/image069.gif) 的定義域為
的定義域為學試卷_理.files/image432.gif) ,
,
學試卷_理.files/image434.gif) …… 1分
…… 1分
學試卷_理.files/image436.gif) 當
當學試卷_理.files/image249.gif) 時,
時, 學試卷_理.files/image439.gif) ,函數(shù)
,函數(shù)學試卷_理.files/image069.gif) 在定義域
在定義域學試卷_理.files/image432.gif) 上單調(diào)遞增. …… 2分
上單調(diào)遞增. …… 2分
(2)①由(Ⅰ)得,當學試卷_理.files/image443.gif) 時,函數(shù)
時,函數(shù)學試卷_理.files/image069.gif) 無極值點.
無極值點.
②學試卷_理.files/image446.gif) 時,
時,學試卷_理.files/image448.gif) 有兩個相同的解
有兩個相同的解學試卷_理.files/image450.gif) ,
,
學試卷_理.files/image452.gif) 時,
時,
學試卷_理.files/image454.gif) 時,函數(shù)
時,函數(shù)學試卷_理.files/image069.gif) 在
在學試卷_理.files/image457.gif) 上無極值點.
…… 3分
上無極值點.
…… 3分
③當學試卷_理.files/image459.gif) 時,
時,學試卷_理.files/image461.gif) 有兩個不同解,
有兩個不同解,
學試卷_理.files/image463.gif)
學試卷_理.files/image465.gif)
學試卷_理.files/image467.gif) 時,
時,學試卷_理.files/image469.gif) ,
,
學試卷_理.files/image471.gif) ,
,
此時 學試卷_理.files/image473.gif) ,
,學試卷_理.files/image069.gif) 隨
隨學試卷_理.files/image143.gif) 在定義域上的變化情況如下表:
在定義域上的變化情況如下表:
學試卷_理.files/image143.gif)
學試卷_理.files/image478.gif)
學試卷_理.files/image480.gif)
學試卷_理.files/image482.gif)
學試卷_理.files/image473.gif)
學試卷_理.files/image485.gif)
學試卷_理.files/image300.gif)
學試卷_理.files/image488.gif)
學試卷_理.files/image069.gif)
減
極小值
增
由此表可知:學試卷_理.files/image491.gif) 時,
時,學試卷_理.files/image069.gif) 有惟一極小值點
有惟一極小值點學試卷_理.files/image494.gif) ,
…… 5分
,
…… 5分
ii) 當學試卷_理.files/image496.gif) 時,0<
時,0<學試卷_理.files/image498.gif) <1
<1
此時,學試卷_理.files/image473.gif) ,
,學試卷_理.files/image069.gif) 隨
隨學試卷_理.files/image143.gif) 的變化情況如下表:
的變化情況如下表:
學試卷_理.files/image143.gif)
學試卷_理.files/image504.gif)
學試卷_理.files/image506.gif)
學試卷_理.files/image508.gif)
學試卷_理.files/image480.gif)
學試卷_理.files/image482.gif)
學試卷_理.files/image473.gif)
學試卷_理.files/image488.gif)
學試卷_理.files/image300.gif)
學試卷_理.files/image485.gif)
學試卷_理.files/image300.gif)
學試卷_理.files/image488.gif)
學試卷_理.files/image069.gif)
增
極大值
減
極小值
增
由此表可知:學試卷_理.files/image496.gif) 時,
時,學試卷_理.files/image069.gif) 有一個極大值
有一個極大值學試卷_理.files/image463.gif) 和一個極小值點
和一個極小值點學試卷_理.files/image519.gif) ;
……
7分
;
……
7分
綜上所述:
當且僅當學試卷_理.files/image521.gif) 時
時學試卷_理.files/image069.gif) 有極值點;
…… 8分
有極值點;
…… 8分
當學試卷_理.files/image524.gif) 時,
時,學試卷_理.files/image069.gif) 有惟一最小值點
有惟一最小值點學試卷_理.files/image526.gif) ;
;
當學試卷_理.files/image496.gif) 時,
時,學試卷_理.files/image069.gif) 有一個極大值點
有一個極大值點學試卷_理.files/image530.gif) 和一個極小值點
和一個極小值點學試卷_理.files/image532.gif)
(3)由(2)可知當學試卷_理.files/image534.gif) 時,函數(shù)
時,函數(shù)學試卷_理.files/image536.gif) ,
,
此時學試卷_理.files/image069.gif) 有惟一極小值點
有惟一極小值點學試卷_理.files/image538.gif)
且學試卷_理.files/image540.gif) …… 9分
…… 9分
學試卷_理.files/image542.gif) …… 11分
…… 11分
令函數(shù)學試卷_理.files/image544.gif)
學試卷_理.files/image546.gif) …… 12分
…… 12分
學試卷_理.files/image548.gif) …… 14分
…… 14分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com