
題目列表(包括答案和解析)
| |||||
 ,動點N(x,y),設直線NP,NQ的斜率分別記為k1,k2,記
,動點N(x,y),設直線NP,NQ的斜率分別記為k1,k2,記 (其中“?”可以是四則運算加、減、乘、除中的任意一種運算),坐標原點為O,點M(2,1).
(其中“?”可以是四則運算加、減、乘、除中的任意一種運算),坐標原點為O,點M(2,1).已知拋物線C:![]() ,過C上一點M,且與M處的切線垂直的直線稱為C在點M的法線.若C在點M的法線的斜率為
,過C上一點M,且與M處的切線垂直的直線稱為C在點M的法線.若C在點M的法線的斜率為![]() ,求點M的坐標(x0,y0);
,求點M的坐標(x0,y0);
已知拋物線C: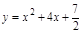 ,過C上一點M,且與M處的切線垂直的直線稱為C在點M的法線.若C在點M的法線的斜率為
,過C上一點M,且與M處的切線垂直的直線稱為C在點M的法線.若C在點M的法線的斜率為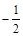 ,求點M的坐標(x0,y0)
,求點M的坐標(x0,y0)
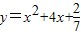 ,過C上一點M,且與M處的切線垂直的直線稱為C在點M的法線.
,過C上一點M,且與M處的切線垂直的直線稱為C在點M的法線. ,求點M的坐標(x,y);
,求點M的坐標(x,y);一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
答案
D
A
A
D
B
C
C
B
C
D
二、填空題
11.
cosx+sinx _ 12.
13._____ -1____________ 14.
15. 16.
16.
17.
三、解答題
18.解:由橢圓的標準方程知橢圓的焦點為 ,離心率為
,離心率為 ………………3分
………………3分
因為雙曲線與橢圓有相同的焦點,所以,雙曲線焦點在x軸上,c=4,………………2分
又雙曲線與橢圓的離心率之和為 ,故雙曲線的離心率為2,所以a=2………………4分
,故雙曲線的離心率為2,所以a=2………………4分
又b2=c2-a2=16-4=12。………………………………………………………………………2分
所以雙曲線的標準方程為 。………………………………………………1分
。………………………………………………1分
19.解:p真:m<0…………………………………………………………………………2分
q真: ……………………………………………………………2分
……………………………………………………………2分
故-1<m<1。…………………………………………………………………………………2分
由 和
和 都是假命題知:p真q假,………………………………………………4分
都是假命題知:p真q假,………………………………………………4分
故 。………………………………4分
。………………………………4分
20.解:(1)設|PF2|=x,則|PF1|=2a-x……………………………………………………2分
∵ ,∴
,∴ , ∴
, ∴ …………1分
…………1分
∴ ,……………………………………………………………………2分
,……………………………………………………………………2分
 ………………………………2分
………………………………2分
(2)由題知a=4, ,故
,故 ………………………………………………1分
………………………………………………1分
由 得
得 ,…………………………………………………………………1分
,…………………………………………………………………1分
又 ……………………………………2分
……………………………………2分
故 ,代入橢圓方程得
,代入橢圓方程得 ,………………………………………2分
,………………………………………2分
故Q點的坐標為 ,
, ,
, ,
, 。
。
…………………………………………………………………………………………………2分
21.解:(1)由函數 ,求導數得
,求導數得 ,…1分
,…1分
由題知點P在切線上,故f(1)=4,…………………………………………………………1分
又切點在曲線上,故1+a+b+c=4①…………………………………………………………1分
且 ,故3+2a+b=3②………………………………………………………………1分
,故3+2a+b=3②………………………………………………………………1分
 ③……………………2分
③……………………2分
 故
故 ……………………1分
……………………1分
(2) …………………………1分
…………………………1分
x

-2




+
0
-
0
+


極大值

極小值

有表格或者分析說明…………………………………………………………………………3分

 ,…………………………………………………………2分
,…………………………………………………………2分
∴f(x)在[-3,1]上最大值為13。故m的取值范圍為{m|m>13}………………………2分
22.解:(1)由題意設過點M的切線方程為: ,…………………………1分
,…………………………1分
代入C得 ,則
,則 ,………………2分
,………………2分
 ,即M(-1,
,即M(-1, ).………………………………………2分
).………………………………………2分
另解:由題意得過點M的切線方程的斜率k=2,…………………………………………1分
設M(x0,y0), ,………………………………………………………………1分
,………………………………………………………………1分
由導數的幾何意義可知2x0+4=2,故x0= -1,……………………………………………2分
代入拋物線可得y0= ,點M的坐標為(-1,
,點M的坐標為(-1, )……………………………………1分
)……………………………………1分
(2)假設在C上存在點 滿足條件.設過Q的切線方程為:
滿足條件.設過Q的切線方程為: ,代入
,代入
 ,
,
則 ,
,
且
 .………………………………………………………2分
.………………………………………………………2分
若 時,由于
時,由于 ,…………………2分
,…………………2分
當a>0時,有
∴  或
或  ;……………………………………2分
;……………………………………2分
當a≤0時,∵k≠0,故 k無解。……………………………………………………1分
若k=0時,顯然 也滿足要求.…………………………………………1分
也滿足要求.…………………………………………1分
綜上,當a>0時,有三個點(-2+ ,
, ),(-2-
),(-2- ,
, )及(-2,-
)及(-2,- ),且過這三點的法線過點P(-2,a),其方程分別為:
),且過這三點的法線過點P(-2,a),其方程分別為:
x+2 y+2-2a
y+2-2a =0,x-2
=0,x-2 y+2+2a
y+2+2a =0,x=-2。
=0,x=-2。
當a≤0時,在C上有一個點(-2,- ),在這點的法線過點P(-2,a),其方程為:x=-2。……………………………………………………………………………………3分
),在這點的法線過點P(-2,a),其方程為:x=-2。……………………………………………………………………………………3分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com