
題目列表(包括答案和解析)

解:(1)點C的坐標為![]() .
.
∵ 點A、B的坐標分別為![]() ,
,
∴ 可設過A、B、C三點的拋物線的解析式為![]() .
.
將![]() 代入拋物線的解析式,得
代入拋物線的解析式,得![]() .
.
∴ 過A、B、C三點的拋物線的解析式為![]() .
.
 (2)可得拋物線的對稱軸為
(2)可得拋物線的對稱軸為![]() ,頂點D的坐標為
,頂點D的坐標為
![]() ,設拋物線的對稱軸與x軸的交點為G.
,設拋物線的對稱軸與x軸的交點為G.
直線BC的解析式為![]() .
.
設點P的坐標為![]() .
.
解法一:如圖8,作OP∥AD交直線BC于點P,
連結AP,作PM⊥x軸于點M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即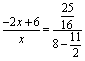 .
.
解得![]() . 經檢驗
. 經檢驗![]() 是原方程的解.
是原方程的解.
此時點P的坐標為![]() .
.
但此時![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四邊形的對邊OP與AD平行但不相等,
∴ 直線BC上不存在符合條件的點P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如圖9,取OA的中點E,作點D關于點E的對稱點P,作PN⊥x軸于
點N. 則∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E點的坐標為
,可得E點的坐標為![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 點P的坐標為![]() .∵ x=
.∵ x=![]() 時,
時,![]() ,
,
∴ 點P不在直線BC上.
∴ 直線BC上不存在符合條件的點P .

(3)![]() 的取值范圍是
的取值范圍是![]() .
.
小明和同桌小聰在課后做作業時,對課本中的一道作業題,進行了認真探索.
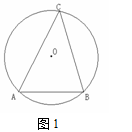
【作業題】如圖1,一個半徑為100m的圓形人工湖如圖所示,弦AB是湖上的一座橋,測得圓周角∠C=45°,求橋AB的長.

小明和小聰經過交流,得到了如下的兩種解決方法:
方法一:延長BO交⊙O與點E,連接AE,得 Rt△ABE,∠E=∠C,∴AB= ;
;
方法二:作AB的弦心距OH,連接OB,
∴∠BOH=∠C,解Rt△OHB,
∴HB= ,∴AB=
,∴AB= .
.
感悟:圓內接三角形的一邊和這邊的對銳角、圓的半徑(或直徑)這三者關系,可構成直角三角形,從而把一邊和這邊的對銳角﹑半徑建立一個關系式.
(1)問題解決:受到(1)的啟發,請你解下面命題:如圖2,點A(3,0)、B(0, ),C為直線AB上一點,過A、O、C的⊙E的半徑為2.求線段OC的長.
),C為直線AB上一點,過A、O、C的⊙E的半徑為2.求線段OC的長.

(2)問題拓展:如圖3,△ABC中,∠ ACB=75°,∠ABC=45°,AB= ,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連結EF, 設⊙O半徑為x, EF為y.①y關于x的函數關系式;②求線段EF長度的最小值.
,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連結EF, 設⊙O半徑為x, EF為y.①y關于x的函數關系式;②求線段EF長度的最小值.

 ;
; ,∴AB=
,∴AB= .
. ),C為直線AB上一點,過A、O、C的⊙E的半徑為2.求線段OC的長.
),C為直線AB上一點,過A、O、C的⊙E的半徑為2.求線段OC的長.
 ,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連結EF, 設⊙O半徑為x, EF為y.①y關于x的函數關系式;②求線段EF長度的最小值.
,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連結EF, 設⊙O半徑為x, EF為y.①y關于x的函數關系式;②求線段EF長度的最小值.
小明和同桌小聰在課后做作業時,對課本中的一道作業題,進行了認真探索。
【作業題】如圖1,一個半徑為100m的圓形人工湖如圖所示,弦AB是湖上的一座橋,測得圓周角∠C=45°,求橋AB的長。
小明和小聰經過交流,得到了如下的兩種解決方法:
方法一:延長BO交⊙O與點E,連接AE,得 Rt△ABE,∠E=∠C,∴AB=100![]() ;
;
方法二:作AB的弦心距OH,連接OB, ∴∠BOH=∠C,解Rt△OHB, ∴HB=50![]() ,
,
∴AB=100![]() 。
。
 感悟:圓內接三角形的一邊和這邊的對銳角、圓的半徑(或直徑)這三者關系,
感悟:圓內接三角形的一邊和這邊的對銳角、圓的半徑(或直徑)這三者關系,
可構成直角三角形,從而把一邊和這邊的對銳角﹑半徑建立一個關系式。
(1)問題解決:受到(1)的啟發,請你解下面命題:如圖2,點A(3,0)、B(0,![]() ),C為直線AB上一點,過A、O、C的⊙E的半徑為2. 求線段OC的長。
),C為直線AB上一點,過A、O、C的⊙E的半徑為2. 求線段OC的長。
(2)問題拓展:如圖3,△ABC中,∠ ACB=75°,∠ABC=45°,AB=2![]() ,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連結EF, 設⊙O半徑為x, EF為y.
,D是線段BC上的一個動點,以AD為直徑畫⊙O分別交AB,AC于E,F,連結EF, 設⊙O半徑為x, EF為y.
① y關于x的函數關系式;②求線段EF長度的最小值。

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com