国产日韩欧美一线二线,美女好全身无遮掩免费网战,亚洲欧美另类卡通乱,日韩av日日夜夜澡,女生抽打女生大骚逼,国产精品99久久…,五月婷婷六月丁香亚洲天堂,中文无码精品一区二区三,日本日p视频免费在线观看

19C.解：由得，所以，所以，因為f(x)=x，所以解得x=-1或-2或2，所以選C

調查某醫院某段時間內嬰兒出生時間與性別的關系，得到以下數據。

	晚上	白天	合計
男嬰	24	31	55
女嬰	8	26	34
合計	32	57	89

試問有多大把握認為嬰兒的性別與出生時間有關系？

已知數列的前項和為，且 (N^*),其中．

(Ⅰ) 求的通項公式；

(Ⅱ) 設 (N^*).

①證明： ；

② 求證：.

【解析】本試題主要考查了數列的通項公式的求解和運用。運用關系式，表示通項公式，然后得到第一問，第二問中利用放縮法得到，②由于，

所以利用放縮法，從此得到結論。

解：(Ⅰ)當時，由得.  ……2分

若存在由得，

從而有，與矛盾，所以.

從而由得得.  ……6分

 (Ⅱ)①證明：

證法一：∵∴

∴ 

∴.…………10分

證法二：，下同證法一.           ……10分

證法三：（利用對偶式）設，，

則.又，也即，所以，也即，又因為，所以.即

                    ………10分

證法四：（數學歸納法）①當時, ,命題成立;

   ②假設時,命題成立,即,

   則當時,

    即

即

故當時，命題成立.

綜上可知，對一切非零自然數，不等式②成立.           ………………10分

②由于，

所以，

從而.

也即

 

⊙O₁和⊙O₂的極坐標方程分別為，．

⑴把⊙O₁和⊙O₂的極坐標方程化為直角坐標方程；

⑵求經過⊙O₁，⊙O₂交點的直線的直角坐標方程．

【解析】本試題主要是考查了極坐標的返程和直角坐標方程的轉化和簡單的圓冤啊位置關系的運用

（1）中，借助于公式，，將極坐標方程化為普通方程即可。

（2）中，根據上一問中的圓的方程，然后作差得到交線所在的直線的普通方程。

解：以極點為原點，極軸為x軸正半軸，建立平面直角坐標系，兩坐標系中取相同的長度單位．

(I)，，由得．所以．

即為⊙O₁的直角坐標方程．

同理為⊙O₂的直角坐標方程．

(II)解法一:由解得，

即⊙O₁，⊙O₂交于點(0,0)和(2,－2)．過交點的直線的直角坐標方程為y=－x．

解法二: 由,兩式相減得－4x-4y=0,即過交點的直線的直角坐標方程為y=－x

 

已知向量，且，A為銳角，求：

（1）角A的大小；

（2）求函數的單調遞增區間和值域．

【解析】第一問中利用，解得   又A為銳角                 

      

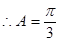
第二問中，

由 解得單調遞增區間為

解：（1）        ……………………3分

   又A為銳角                 

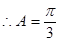                              ……………………5分

（2）

                                                  ……………………8分

  由 解得單調遞增區間為

                                                  ……………………10分

 

 

（天津卷理12）一個正方體的各定點均在同一球的球面上，若該球的體積為，則該正方體的表面積為                    .

解析：由得，所以，表面積為.