
題目列表(包括答案和解析)
已知集合A={y|y=log2x, x>1},B={y|y=(![]() )x, 0<x<1},則A∩B等于 ( )
)x, 0<x<1},則A∩B等于 ( )
A.{y|0<y<![]() } B.{y|0<y<1} C.{y|
} B.{y|0<y<1} C.{y|![]() <y<1} D.
<y<1} D. ![]()
函數(shù)y=![]() 的定義域是:
的定義域是:
A.{x|0<x<2} B.{x|0<x<1或1<x≤2} C.{x|0<x≤2} D.{x|0<x<1或1<x<2}
已知集合A={x|-l≤x≤3},集合B=|x|log2x<2},則A B=
B=
A.{x|1≤x≤3} B.{x|-1≤x≤3}
C.{x| 0<x≤3} D.{x|-1≤x<0}
若f (x)是偶函數(shù),且當(dāng)x∈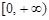 時(shí),f
(x) = x-1,則f (x-1) < 0的解集是( )
時(shí),f
(x) = x-1,則f (x-1) < 0的解集是( )
A.{x |-1 < x < 0} B.{x | x < 0或1< x < 2}
C.{x | 0 < x < 2} D.{x | 1 < x < 2}
不等式|2x -l|-x<1的解集是
A.{x|0<x<2} B.{x|l<x<2} C.{x|0<x<1} D.{x|l<x<3}
x+2y >1
一、1. A 2.B 3.B 4.C 5.A 6.D 7.A 8.C 9.B 10.A 11.D 12.D
二、13.1 14.1 15.r≥6 16.81
三、
縣一中2006年高考數(shù)學(xué)模擬卷.files\image169.gif) 18. (1)設(shè) A為
“甲預(yù)報(bào)站預(yù)報(bào)準(zhǔn)確”B為“乙預(yù)報(bào)站預(yù)報(bào)準(zhǔn)確”則在同一時(shí)間段里至少
18. (1)設(shè) A為
“甲預(yù)報(bào)站預(yù)報(bào)準(zhǔn)確”B為“乙預(yù)報(bào)站預(yù)報(bào)準(zhǔn)確”則在同一時(shí)間段里至少
有一個(gè)預(yù)報(bào)準(zhǔn)確的概率為縣一中2006年高考數(shù)學(xué)模擬卷.files\image171.gif) -------4分
-------4分
(2)①縣一中2006年高考數(shù)學(xué)模擬卷.files\image173.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image121.gif) 的分布列為
的分布列為
縣一中2006年高考數(shù)學(xué)模擬卷.files\image121.gif)
0
1
2
3
p
0.008
0.096
0.384
0.512
縣一中2006年高考數(shù)學(xué)模擬卷.files\image175.gif) 分
分
②由縣一中2006年高考數(shù)學(xué)模擬卷.files\image123.gif) 在
在縣一中2006年高考數(shù)學(xué)模擬卷.files\image125.gif) 上的值恒為正值得
上的值恒為正值得縣一中2006年高考數(shù)學(xué)模擬卷.files\image178.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image180.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image182.gif) ---12分
---12分
19. 解法一
(1)證明:連AC交DB于點(diǎn)O,
由正四棱柱性質(zhì)可知AA1⊥底面ABCD,AC⊥BD,∴A
又∵A1B1⊥側(cè)面BC1且BC1⊥BE ∴A
又∵BD∩BE=B,∴A
(2)設(shè)A
在側(cè)面BC1中,BE⊥B
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image184.gif) 又BC=2,BB1=4,∴CE=1.
又BC=2,BB1=4,∴CE=1.
連OE,則OE為平面ACC
在RtㄓECO中,縣一中2006年高考數(shù)學(xué)模擬卷.files\image186.gif) ,∴
,∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image188.gif)
又縣一中2006年高考數(shù)學(xué)模擬卷.files\image190.gif) ∵
∵縣一中2006年高考數(shù)學(xué)模擬卷.files\image192.gif)
又縣一中2006年高考數(shù)學(xué)模擬卷.files\image194.gif) ,∴
,∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image196.gif) 在RtㄓA1BK中,
在RtㄓA1BK中,縣一中2006年高考數(shù)學(xué)模擬卷.files\image198.gif) ,即為A1B與平面BDE所成的角的正弦值.
,即為A1B與平面BDE所成的角的正弦值.
解法二:
(1) 以D為原點(diǎn),DA、DC、DD1所在的直線分別為x,y,z軸建立空間直角坐標(biāo)系縣一中2006年高考數(shù)學(xué)模擬卷.files\image200.gif) .
.
D(0,0,0), A(2,0,0),B(2,2,0),C(0,2,0)
A1(2,0,4),B1(2,2,4),C1(0,2,4),D1(0,0,4),設(shè)點(diǎn)E(0,2,t)
∵BE⊥B縣一中2006年高考數(shù)學(xué)模擬卷.files\image202.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image204.gif) ,∴E(0,2,1)
,∴E(0,2,1)
又縣一中2006年高考數(shù)學(xué)模擬卷.files\image206.gif) ,
,縣一中2006年高考數(shù)學(xué)模擬卷.files\image208.gif) ,
,縣一中2006年高考數(shù)學(xué)模擬卷.files\image210.gif)
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image212.gif)
∴A
(2)設(shè)A
則縣一中2006年高考數(shù)學(xué)模擬卷.files\image214.gif)
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image216.gif) ∴
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image218.gif)
由縣一中2006年高考數(shù)學(xué)模擬卷.files\image220.gif) ⊥
⊥ 縣一中2006年高考數(shù)學(xué)模擬卷.files\image222.gif) 得
得縣一中2006年高考數(shù)學(xué)模擬卷.files\image224.gif)
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image226.gif) ,…………①
,…………①
縣一中2006年高考數(shù)學(xué)模擬卷.files\image228.gif) 同理有
同理有縣一中2006年高考數(shù)學(xué)模擬卷.files\image220.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image231.gif) 得
得縣一中2006年高考數(shù)學(xué)模擬卷.files\image233.gif)
…②
由①②聯(lián)立,解得縣一中2006年高考數(shù)學(xué)模擬卷.files\image235.gif) ∴
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image237.gif)
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image239.gif) ,又易知
,又易知縣一中2006年高考數(shù)學(xué)模擬卷.files\image241.gif)
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image243.gif) ,即所求角的正弦值為
,即所求角的正弦值為縣一中2006年高考數(shù)學(xué)模擬卷.files\image245.gif) .
.
20.解:(1)易得縣一中2006年高考數(shù)學(xué)模擬卷.files\image247.gif) .
.
(2)設(shè)P縣一中2006年高考數(shù)學(xué)模擬卷.files\image249.gif) 為
為縣一中2006年高考數(shù)學(xué)模擬卷.files\image135.gif) 的圖像上任一點(diǎn),點(diǎn)P關(guān)于直線
的圖像上任一點(diǎn),點(diǎn)P關(guān)于直線縣一中2006年高考數(shù)學(xué)模擬卷.files\image138.gif) 的對(duì)稱點(diǎn)為
的對(duì)稱點(diǎn)為縣一中2006年高考數(shù)學(xué)模擬卷.files\image253.gif)
∵點(diǎn)縣一中2006年高考數(shù)學(xué)模擬卷.files\image253.gif) 在
在縣一中2006年高考數(shù)學(xué)模擬卷.files\image132.gif) 的圖像上,
的圖像上,
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image256.gif) ,即得
,即得縣一中2006年高考數(shù)學(xué)模擬卷.files\image258.gif) .
.
(3)縣一中2006年高考數(shù)學(xué)模擬卷.files\image260.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image262.gif) 下面求
下面求縣一中2006年高考數(shù)學(xué)模擬卷.files\image143.gif) 的最小值:
的最小值:
①當(dāng)縣一中2006年高考數(shù)學(xué)模擬卷.files\image265.gif) ,即
,即縣一中2006年高考數(shù)學(xué)模擬卷.files\image267.gif) 時(shí)
時(shí)縣一中2006年高考數(shù)學(xué)模擬卷.files\image269.gif)
由縣一中2006年高考數(shù)學(xué)模擬卷.files\image271.gif) ,得
,得縣一中2006年高考數(shù)學(xué)模擬卷.files\image273.gif) ,所以
,所以縣一中2006年高考數(shù)學(xué)模擬卷.files\image275.gif) .
.
②當(dāng)縣一中2006年高考數(shù)學(xué)模擬卷.files\image277.gif) 即
即縣一中2006年高考數(shù)學(xué)模擬卷.files\image279.gif) 時(shí)
時(shí)縣一中2006年高考數(shù)學(xué)模擬卷.files\image143.gif) 在R上是增函數(shù),無(wú)最小值,與
在R上是增函數(shù),無(wú)最小值,與縣一中2006年高考數(shù)學(xué)模擬卷.files\image281.gif) 不符.
不符.
③當(dāng)縣一中2006年高考數(shù)學(xué)模擬卷.files\image283.gif) 即
即縣一中2006年高考數(shù)學(xué)模擬卷.files\image285.gif) 時(shí),
時(shí),縣一中2006年高考數(shù)學(xué)模擬卷.files\image143.gif) 在R上是減函數(shù),無(wú)最小值,與
在R上是減函數(shù),無(wú)最小值,與縣一中2006年高考數(shù)學(xué)模擬卷.files\image281.gif) 不符.
不符.
④當(dāng)縣一中2006年高考數(shù)學(xué)模擬卷.files\image287.gif) 即
即縣一中2006年高考數(shù)學(xué)模擬卷.files\image289.gif) 時(shí),
時(shí),縣一中2006年高考數(shù)學(xué)模擬卷.files\image291.gif) ,與最小值
,與最小值縣一中2006年高考數(shù)學(xué)模擬卷.files\image293.gif) 不符.
不符.
綜上所述,所求縣一中2006年高考數(shù)學(xué)模擬卷.files\image149.gif) 的取值范圍是
的取值范圍是縣一中2006年高考數(shù)學(xué)模擬卷.files\image275.gif) .
.
21.(1)解:設(shè)P(a,0),Q(0,b)則:縣一中2006年高考數(shù)學(xué)模擬卷.files\image297.gif) ∴
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image299.gif)
設(shè)M(x,y)∵縣一中2006年高考數(shù)學(xué)模擬卷.files\image301.gif) ∴
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image303.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image305.gif) ∴
∴縣一中2006年高考數(shù)學(xué)模擬卷.files\image307.gif)
(2)解法一:設(shè)A(a,b),縣一中2006年高考數(shù)學(xué)模擬卷.files\image309.gif) ,
,縣一中2006年高考數(shù)學(xué)模擬卷.files\image311.gif) (x1≠x2)
(x1≠x2)
則直線SR的方程為:縣一中2006年高考數(shù)學(xué)模擬卷.files\image313.gif) ,即4y = (x1+x2)x-x1x2
,即4y = (x1+x2)x-x1x2
∵A點(diǎn)在SR上,∴4b=(x1+x2)a-x1x2 ①
對(duì)縣一中2006年高考數(shù)學(xué)模擬卷.files\image307.gif) 求導(dǎo)得:y′=
求導(dǎo)得:y′=縣一中2006年高考數(shù)學(xué)模擬卷.files\image316.gif) x
x
∴拋物線上S.R處的切線方程為
縣一中2006年高考數(shù)學(xué)模擬卷.files\image318.gif) 即4
即4縣一中2006年高考數(shù)學(xué)模擬卷.files\image320.gif) ②
②
縣一中2006年高考數(shù)學(xué)模擬卷.files\image322.gif) 即4
即4縣一中2006年高考數(shù)學(xué)模擬卷.files\image324.gif) ③
③
聯(lián)立②、③得 縣一中2006年高考數(shù)學(xué)模擬卷.files\image326.gif)
代入①得:ax-2y-2b=0故:B點(diǎn)在直線ax-2y-2b=0上.
解法二:設(shè)A(a,b),當(dāng)過(guò)點(diǎn)A的直線斜率不存在時(shí)l與拋物線有且僅有一個(gè)公共點(diǎn),與題意不符,可設(shè)直線SR的方程為y-b=k(x-a).
與縣一中2006年高考數(shù)學(xué)模擬卷.files\image307.gif) 聯(lián)立消去y,得x2-4kx+4ak-4b=0.設(shè)
聯(lián)立消去y,得x2-4kx+4ak-4b=0.設(shè)縣一中2006年高考數(shù)學(xué)模擬卷.files\image309.gif) ,
,縣一中2006年高考數(shù)學(xué)模擬卷.files\image311.gif) (x1≠x2)
(x1≠x2)
則由韋達(dá)定理,得縣一中2006年高考數(shù)學(xué)模擬卷.files\image330.gif)
又過(guò)S、R點(diǎn)的切線方程分別為縣一中2006年高考數(shù)學(xué)模擬卷.files\image332.gif) ,
,縣一中2006年高考數(shù)學(xué)模擬卷.files\image334.gif) .
.
聯(lián)立,并解之,得縣一中2006年高考數(shù)學(xué)模擬卷.files\image336.gif) (k為參數(shù)) 消去k,得ax-2y-2b=0.
(k為參數(shù)) 消去k,得ax-2y-2b=0.
故B點(diǎn)在直線2ax-y-b=0上.
22.解:(1)縣一中2006年高考數(shù)學(xué)模擬卷.files\image161.gif) =22;
=22;
縣一中2006年高考數(shù)學(xué)模擬卷.files\image338.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image340.gif)
(3)由(2)知縣一中2006年高考數(shù)學(xué)模擬卷.files\image342.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image344.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image346.gif) =
=縣一中2006年高考數(shù)學(xué)模擬卷.files\image348.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image350.gif)
縣一中2006年高考數(shù)學(xué)模擬卷.files\image352.gif) .
.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com