
題目列表(包括答案和解析)
函數(shù)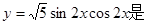 (
)
(
)
A.周期為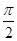 的奇函數(shù)
B.周期為
的奇函數(shù)
B.周期為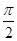 的偶函數(shù)
的偶函數(shù)
C.周期為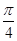 的奇函數(shù)
D.周期為
的奇函數(shù)
D.周期為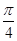 的偶函數(shù)
的偶函數(shù)
函數(shù)![]() ( )
( )
A.周期為![]() 的奇函數(shù) B.周期為
的奇函數(shù) B.周期為![]() 的偶函數(shù)
的偶函數(shù)
C.周期為![]() 的奇函數(shù) D.周期為
的奇函數(shù) D.周期為![]() 的偶函數(shù)
的偶函數(shù)
| A、周期為π的奇函數(shù) | ||
| B、周期為π的偶函數(shù) | ||
C、周期為
| ||
D、周期為
|
| π |
| 4 |
| π |
| 4 |
| A、周期為π的奇函數(shù) |
| B、周期為π的偶函數(shù) |
| C、周期為2π的奇函數(shù) |
| D、周期為2π的偶函數(shù) |
| π |
| 4 |
| A、最小正周期為π的奇函數(shù) | ||
| B、最小正周期為π的偶函數(shù) | ||
C、最小正周期為
| ||
D、最小正周期為
|
一、選擇題:(本大題共10小題,每小題5分,共50分)
1第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) B
B 第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) A 3
A 3第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文C(理C) 4
文C(理C) 4第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) D 5
D 5第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文A(理B) 6
文A(理B) 6第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文B(理C) 7
文B(理C) 7第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文C(理C) 8
文C(理C) 8第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文C(理A) 9
文C(理A) 9第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文A (理D) 10
文A (理D) 10第三次六校聯(lián)考數(shù)學(xué)試卷.files\image002.gif) 文D(理A)
文D(理A)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image237.gif) 三、解答題:(本大題共6個(gè)解答題,滿分76分,)
三、解答題:(本大題共6個(gè)解答題,滿分76分,)
線為y軸建立平面直角坐標(biāo)系如圖所示,
則A(-4,0),N(4,0),設(shè)P(x,y) 第三次六校聯(lián)考數(shù)學(xué)試卷.files\image239.gif)
由|PM|:|PN|=第三次六校聯(lián)考數(shù)學(xué)試卷.files\image169.gif) ,|PM|2=|PA|2 ?|MA|2得:
,|PM|2=|PA|2 ?|MA|2得:
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image242.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image244.gif)
代入坐標(biāo)得:第三次六校聯(lián)考數(shù)學(xué)試卷.files\image246.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image248.gif)
整理得:第三次六校聯(lián)考數(shù)學(xué)試卷.files\image250.gif)
即第三次六校聯(lián)考數(shù)學(xué)試卷.files\image252.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image254.gif)
所以動(dòng)點(diǎn)P的軌跡是以點(diǎn)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image256.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image258.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image260.gif)
(理)解:(I)當(dāng)a=1時(shí) 第三次六校聯(lián)考數(shù)學(xué)試卷.files\image262.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image264.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image266.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image239.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image269.gif) 或
或第三次六校聯(lián)考數(shù)學(xué)試卷.files\image271.gif) 或
或第三次六校聯(lián)考數(shù)學(xué)試卷.files\image273.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image275.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image277.gif) 或
或第三次六校聯(lián)考數(shù)學(xué)試卷.files\image279.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image281.gif)
(II)原不等式第三次六校聯(lián)考數(shù)學(xué)試卷.files\image283.gif)
設(shè)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image285.gif) 有
有第三次六校聯(lián)考數(shù)學(xué)試卷.files\image287.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image289.gif)
當(dāng)且僅當(dāng)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image291.gif)
即第三次六校聯(lián)考數(shù)學(xué)試卷.files\image293.gif) 時(shí)
時(shí)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image295.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image297.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image303.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image305.gif)
解得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image307.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image309.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image311.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image313.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image315.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image317.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image289.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image320.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image322.gif)
若由方程組第三次六校聯(lián)考數(shù)學(xué)試卷.files\image324.gif) 解得
解得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image326.gif) ,可參考給分
,可參考給分
(理)解:(Ⅰ)設(shè)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image328.gif) (a≠0),則
(a≠0),則
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image330.gif) …… ①
…… ①
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image332.gif) …… ②
…… ②
又∵第三次六校聯(lián)考數(shù)學(xué)試卷.files\image334.gif) 有兩等根
有兩等根
∴第三次六校聯(lián)考數(shù)學(xué)試卷.files\image336.gif) …… ③
…… ③
由①②③得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image338.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image244.gif)
又∵第三次六校聯(lián)考數(shù)學(xué)試卷.files\image341.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image343.gif)
∴a<0, 故第三次六校聯(lián)考數(shù)學(xué)試卷.files\image345.gif)
∴第三次六校聯(lián)考數(shù)學(xué)試卷.files\image347.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image248.gif)
(Ⅱ)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image350.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image352.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image354.gif)
∵g(x)無(wú)極值
∴方程第三次六校聯(lián)考數(shù)學(xué)試卷.files\image356.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image358.gif)
得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image360.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image264.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image266.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image239.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image269.gif) 或
或第三次六校聯(lián)考數(shù)學(xué)試卷.files\image271.gif) 或
或第三次六校聯(lián)考數(shù)學(xué)試卷.files\image273.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image275.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image277.gif) 或
或第三次六校聯(lián)考數(shù)學(xué)試卷.files\image279.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image281.gif)
(II)原不等式第三次六校聯(lián)考數(shù)學(xué)試卷.files\image283.gif)
設(shè)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image285.gif) 有
有第三次六校聯(lián)考數(shù)學(xué)試卷.files\image287.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image289.gif)
當(dāng)且僅當(dāng)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image291.gif)
即第三次六校聯(lián)考數(shù)學(xué)試卷.files\image293.gif) 時(shí)
時(shí)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image295.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image297.gif)
(理)解:以AN所在直線為x軸,AN的中垂
線為y軸建立平面直角坐標(biāo)系如圖所示,
則A(-4,0),N(4,0),設(shè)P(x,y) 第三次六校聯(lián)考數(shù)學(xué)試卷.files\image239.gif)
由|PM|:|PN|=第三次六校聯(lián)考數(shù)學(xué)試卷.files\image169.gif) ,|PM|2=|PA|2 ?|MA|2得:
,|PM|2=|PA|2 ?|MA|2得:
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image242.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image244.gif)
代入坐標(biāo)得:第三次六校聯(lián)考數(shù)學(xué)試卷.files\image246.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image248.gif)
整理得:第三次六校聯(lián)考數(shù)學(xué)試卷.files\image250.gif)
即第三次六校聯(lián)考數(shù)學(xué)試卷.files\image252.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image254.gif)
所以動(dòng)點(diǎn)P的軌跡是以點(diǎn)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image256.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image258.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image260.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image330.gif) …… ①
…… ①
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image332.gif) …… ②
…… ②
又∵第三次六校聯(lián)考數(shù)學(xué)試卷.files\image334.gif) 有兩等根
有兩等根
∴第三次六校聯(lián)考數(shù)學(xué)試卷.files\image336.gif) …… ③
…… ③
由①②③得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image338.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image244.gif)
又∵第三次六校聯(lián)考數(shù)學(xué)試卷.files\image341.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image343.gif)
∴a<0, 故第三次六校聯(lián)考數(shù)學(xué)試卷.files\image345.gif)
∴第三次六校聯(lián)考數(shù)學(xué)試卷.files\image347.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image248.gif)
(Ⅱ)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image350.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image352.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image354.gif)
∵g(x)無(wú)極值
∴方程第三次六校聯(lián)考數(shù)學(xué)試卷.files\image356.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image358.gif)
得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image360.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image260.gif)
(理)解:(I)設(shè)第三次六校聯(lián)考數(shù)學(xué)試卷.files\image364.gif) (1)
(1)
又第三次六校聯(lián)考數(shù)學(xué)試卷.files\image366.gif) 故
故第三次六校聯(lián)考數(shù)學(xué)試卷.files\image368.gif) (2)
(2)
由(1),(2)解得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image370.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image275.gif)
(II)由向量第三次六校聯(lián)考數(shù)學(xué)試卷.files\image202.gif) 與向量
與向量第三次六校聯(lián)考數(shù)學(xué)試卷.files\image205.gif) 的夾角為
的夾角為第三次六校聯(lián)考數(shù)學(xué)試卷.files\image207.gif) 得
得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image373.gif)
由第三次六校聯(lián)考數(shù)學(xué)試卷.files\image375.gif) 及A+B+C=
及A+B+C=第三次六校聯(lián)考數(shù)學(xué)試卷.files\image036.gif) 知A+C=
知A+C=第三次六校聯(lián)考數(shù)學(xué)試卷.files\image378.gif)
則第三次六校聯(lián)考數(shù)學(xué)試卷.files\image380.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image281.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image383.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image343.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image385.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image387.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image354.gif)
由0<A<第三次六校聯(lián)考數(shù)學(xué)試卷.files\image378.gif) 得
得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image391.gif) ,得
,得第三次六校聯(lián)考數(shù)學(xué)試卷.files\image393.gif)
故第三次六校聯(lián)考數(shù)學(xué)試卷.files\image211.gif) 的取值范圍是
的取值范圍是第三次六校聯(lián)考數(shù)學(xué)試卷.files\image395.gif)
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image322.gif)
Sn+1=2an+1-3(n+1),兩式相減并整理得:an+1=2an+3
第三次六校聯(lián)考數(shù)學(xué)試卷.files\image239.gif)
所以3+ an+1=2(3+an),又a1=S1=2a1-3,a1=3可知3+
a1=6第三次六校聯(lián)考數(shù)學(xué)試卷.files\image399.gif) ,進(jìn)而可知an+3
,進(jìn)而可知an+3第三次六校聯(lián)考數(shù)學(xué)試卷.files\image399.gif)
所以第三次六校聯(lián)考數(shù)學(xué)試卷.files\image401.gif) ,故數(shù)列{3+an}是首相為6,公比為2的等比數(shù)列,
,故數(shù)列{3+an}是首相為6,公比為2的等比數(shù)列,
所以3+an=6第三次六校聯(lián)考數(shù)學(xué)試卷.files\image403.gif) ,即an=3(
,即an=3(第三次六校聯(lián)考數(shù)學(xué)試卷.files\image405.gif) )
)
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com