題目列表(包括答案和解析)
12、已知函數f（x）是定義在R上的函數，如果函數f（x）在R上的導函數f′（x）的圖象如圖，則有以下幾個命題：已知函數f(x)是定義在R上的函數，如果函數f(x)在R上的導函數f′(x)的圖象如圖，則有以下幾個命題：
(1)f(x)的單調遞減區間是(－2,0)、(2，＋∞)，f(x)的單調遞增區間是(－∞，－2)、(0,2)；
(2)f(x)只在x＝－2處取得極大值；
(3)f(x)在x＝－2與x＝2處取得極大值；
(4)f(x)在x＝0處取得極小值．
其中正確命題的個數為 ( )
| A．1 | B．2 |
| C．3 | D．4 |
已知函數f(x)是定義在R上的函數，如果函數f(x)在R上的導函數f′(x)的圖象如圖，則有以下幾個命題：
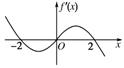
(1)f(x)的單調遞減區間是(－2,0)、(2，＋∞)，f(x)的單調遞增區間是(－∞，－2)、(0,2)；
(2)f(x)只在x＝－2處取得極大值；
(3)f(x)在x＝－2與x＝2處取得極大值；
(4)f(x)在x＝0處取得極小值．
其中正確命題的個數為 ( )
A．1 B．2
C．3 D．4
（08年鷹潭市二模理）有以下幾個命題
①曲線
按
平移可得曲線
；
②直線AB與平面
相交于點B，且AB與內相交于點C的三條互不重合的直線CD、CE、CF所成的角相等，則AB⊥；
③已知橢圓
與雙曲線
有相同的準線，則動點
的軌跡為直線
④若直線
在平面
內的射影依次為一個點和一條直線，且
，則
；
⑤設A、B為平面上兩個定點，P為動點，若
，則動點P的軌跡為圓
其中真命題的序號為 ;（寫出所有真命題的序號）
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)-f(x2) |
| x1-x2 |
一、選擇題：(本大題共10小題,每小題5分,共50分)
1
B A 3 文C（理C） 4
D 5 文A（理B） 6 文B（理C） 7 文C（理C） 8 文C（理A） 9 文A （理D） 10 文D（理A）
二、填空題：（本大題共6小題，每小題4分，共24分 ）
11 （文）“若
，則
” ，（理）
12 （文）
，（理）
，
13 （文），（理）－2
14
-2 15 
16 ②④
三、解答題：（本大題共6個解答題，滿分76分，）
17 （文）解：以AN所在直線為x軸，AN的中垂
線為y軸建立平面直角坐標系如圖所示，
則A(-4,0),N(4,0),設P（x，y） 
由|PM|：|PN|=
，|PM|2=|PA|2 ?|MA|2得：
代入坐標得：
整理得：
即
所以動點P的軌跡是以點
（理）解：(I)當a=1時 
或
或
或
(II)原不等式
設
有
當且僅當
即
時
依題有：10a<10 ∴
為所求
18 （文）解：
解得
若由方程組
解得
，可參考給分
（理）解：(Ⅰ)設
（a≠0），則
…… ①
…… ②
又∵
有兩等根
∴
…… ③
由①②③得
又∵
∴a<0, 故
∴
(Ⅱ)
∵g(x)無極值
∴方程
得
19 （文）解：(I)當a=1時
或或
或
(II)原不等式
設有
當且僅當
即時
依題有：10a<10 ∴為所求
（理）解：以AN所在直線為x軸，AN的中垂
線為y軸建立平面直角坐標系如圖所示，
則A(-4,0),N(4,0),設P（x，y）
由|PM|：|PN|=，|PM|2=|PA|2 ?|MA|2得：
代入坐標得：
整理得：
即
所以動點P的軌跡是以點
20 （文）解：(Ⅰ)設 （a≠0），則
…… ①
…… ②
又∵有兩等根
∴…… ③
由①②③得
又∵
∴a<0, 故
∴
(Ⅱ)
∵g(x)無極值
∴方程
得
（理）解：（I）設
（1）
又
故
（2）
由（1），（2）解得
（II）由向量
與向量
的夾角為
得
由
及A+B+C=
知A+C=
則
由0<A<得
，得
故
的取值范圍是
21 解：（I）由已知得Sn=2an-3n，
Sn+1=2an+1-3(n+1),兩式相減并整理得：an+1=2an+3
所以3+ an+1=2（3+an），又a1=S1=2a1-3，a1=3可知3+
a1=6
，進而可知an+3
所以
，故數列{3+an}是首相為6，公比為2的等比數列，
所以3+an=6
,即an=3(
)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com