
題目列表(包括答案和解析)
若函數(shù) 的圖象與
的圖象與 軸交于點(diǎn)
軸交于點(diǎn) ,過點(diǎn)
,過點(diǎn) 的直線
的直線 與函數(shù)的圖象交于
與函數(shù)的圖象交于 、
、 兩點(diǎn),則
兩點(diǎn),則 (其中O為坐標(biāo)原點(diǎn)) ( )
(其中O為坐標(biāo)原點(diǎn)) ( )
A. | B. | C. | D. |
 的圖象與
的圖象與 軸交于點(diǎn)
軸交于點(diǎn) ,過點(diǎn)
,過點(diǎn) 的直線
的直線 與函數(shù)的圖象交于
與函數(shù)的圖象交于 、
、 兩點(diǎn),則
兩點(diǎn),則 (其中O為坐標(biāo)原點(diǎn)) ( )
(其中O為坐標(biāo)原點(diǎn)) ( )A. | B. | C. | D. |
若函數(shù) 的圖象與x軸交于點(diǎn)
的圖象與x軸交于點(diǎn)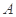 ,過點(diǎn)
,過點(diǎn)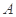 的直線
的直線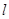 與函數(shù)
與函數(shù)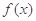 的圖象交于
的圖象交于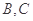 兩點(diǎn),則
兩點(diǎn),則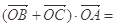 (
)
(
)
A.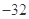 B.16 C.32 D.
B.16 C.32 D.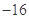
若函數(shù)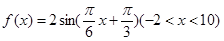 的圖象與x軸交于點(diǎn)A,過點(diǎn)A的直線與函數(shù)的圖象交于B、C兩點(diǎn),則
的圖象與x軸交于點(diǎn)A,過點(diǎn)A的直線與函數(shù)的圖象交于B、C兩點(diǎn),則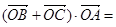
A.-32 B.-16 C.16 D.32
若函數(shù)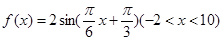 的圖象與x軸交于點(diǎn)A,過點(diǎn)A的直線
的圖象與x軸交于點(diǎn)A,過點(diǎn)A的直線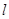 與函數(shù)的圖象交于B、C兩點(diǎn),則
與函數(shù)的圖象交于B、C兩點(diǎn),則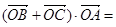 ( )
( )
A.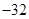 B.
B.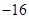 C.
C.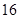 D.
D.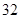
1.B 2.A 3.C 4.B 5.A 6.D 7.B 8.C 9.C 1 0.B
11.B 12.D
1.理科數(shù)學(xué).files/image298.gif) .
.
2.理科數(shù)學(xué).files/image300.gif)
3.理科數(shù)學(xué).files/image302.gif) 是方程
是方程理科數(shù)學(xué).files/image304.gif) 的根,
的根,理科數(shù)學(xué).files/image306.gif) 或8,又
或8,又理科數(shù)學(xué).files/image308.gif) ,
,
理科數(shù)學(xué).files/image310.gif) .
.
4.理科數(shù)學(xué).files/image312.gif) .
.
5.畫出可行域,如圖,理科數(shù)學(xué).files/image045.gif) 可看為區(qū)域內(nèi)的點(diǎn)與(0,0)連線的斜率,
可看為區(qū)域內(nèi)的點(diǎn)與(0,0)連線的斜率,理科數(shù)學(xué).files/image315.gif) .
.
理科數(shù)學(xué).files/image317.gif) .
.
6.理科數(shù)學(xué).files/image319.gif)
7.在理科數(shù)學(xué).files/image321.gif) 中,
中,理科數(shù)學(xué).files/image323.gif) ,在
,在理科數(shù)學(xué).files/image325.gif) 中,
中,理科數(shù)學(xué).files/image327.gif) ,
,
在理科數(shù)學(xué).files/image329.gif) 中,
中,理科數(shù)學(xué).files/image331.gif) ,在
,在理科數(shù)學(xué).files/image333.gif) 中,
中,理科數(shù)學(xué).files/image335.gif) ,
,理科數(shù)學(xué).files/image337.gif) .
.
8.理科數(shù)學(xué).files/image075.gif) 的圖象如圖所示
的圖象如圖所示
理科數(shù)學(xué).files/image340.gif) 的解集為
的解集為理科數(shù)學(xué).files/image088.gif) .
.
9.由理科數(shù)學(xué).files/image097.gif) 知
知理科數(shù)學(xué).files/image063.gif) 點(diǎn)的軌跡是以
點(diǎn)的軌跡是以理科數(shù)學(xué).files/image177.gif) ,
,理科數(shù)學(xué).files/image346.gif) 為焦點(diǎn)的雙曲線一支.
為焦點(diǎn)的雙曲線一支.理科數(shù)學(xué).files/image348.gif) ,
,理科數(shù)學(xué).files/image350.gif) .
.
10.由獨(dú)立重復(fù)試驗(yàn)的概率理科數(shù)學(xué).files/image352.gif) .
.
11.設(shè)理科數(shù)學(xué).files/image354.gif) ,圓為
,圓為理科數(shù)學(xué).files/image356.gif) 最長弦
最長弦理科數(shù)學(xué).files/image119.gif) 為直徑,最短弦
為直徑,最短弦理科數(shù)學(xué).files/image121.gif) 的中點(diǎn)為
的中點(diǎn)為理科數(shù)學(xué).files/image360.gif) ,
,
理科數(shù)學(xué).files/image362.gif)
理科數(shù)學(xué).files/image364.gif)
12.幾何體的表面積是三個(gè)圓心角為理科數(shù)學(xué).files/image141.gif) 、半徑為1的扇形面積與半徑為1的球面積的
、半徑為1的扇形面積與半徑為1的球面積的理科數(shù)學(xué).files/image367.gif) 之和,即表面積為
之和,即表面積為理科數(shù)學(xué).files/image369.gif) .
.
二、
13.理科數(shù)學(xué).files/image371.gif) 平方得
平方得理科數(shù)學(xué).files/image373.gif)
理科數(shù)學(xué).files/image375.gif) .
.
14.理科數(shù)學(xué).files/image377.gif) 的系數(shù)
的系數(shù)理科數(shù)學(xué).files/image379.gif)
15.1.理科數(shù)學(xué).files/image381.gif) 與
與理科數(shù)學(xué).files/image383.gif) 互為反函數(shù),
互為反函數(shù),
令理科數(shù)學(xué).files/image385.gif) ,
,
理科數(shù)學(xué).files/image387.gif) .
.
16.0或 理科數(shù)學(xué).files/image389.gif) ,設(shè)
,設(shè)理科數(shù)學(xué).files/image177.gif) 點(diǎn)的橫坐標(biāo)為
點(diǎn)的橫坐標(biāo)為理科數(shù)學(xué).files/image392.gif) 點(diǎn)處的切線斜率為
點(diǎn)處的切線斜率為理科數(shù)學(xué).files/image394.gif) ,由夾角公式得
,由夾角公式得理科數(shù)學(xué).files/image396.gif) ,即
,即理科數(shù)學(xué).files/image398.gif)
若理科數(shù)學(xué).files/image400.gif) ,得
,得理科數(shù)學(xué).files/image402.gif) ,矛盾
,矛盾
若理科數(shù)學(xué).files/image404.gif)
理科數(shù)學(xué).files/image406.gif) 或
或理科數(shù)學(xué).files/image408.gif) .
.
三、
17.(1)理科數(shù)學(xué).files/image410.gif) ,由
,由理科數(shù)學(xué).files/image412.gif) ,得
,得理科數(shù)學(xué).files/image414.gif) ,消去
,消去理科數(shù)學(xué).files/image416.gif) 得
得理科數(shù)學(xué).files/image418.gif)
理科數(shù)學(xué).files/image420.gif) .
.
理科數(shù)學(xué).files/image422.gif) .
.
(2)理科數(shù)學(xué).files/image424.gif)
理科數(shù)學(xué).files/image426.gif)
理科數(shù)學(xué).files/image428.gif) ,
,
理科數(shù)學(xué).files/image430.gif) .
.
理科數(shù)學(xué).files/image432.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image434.gif) 的最大值為
的最大值為理科數(shù)學(xué).files/image436.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image434.gif) 的最大值為2.
的最大值為2.
18.(1)從3種服裝商品、2種家電商品,4種日用商品中,選出3種商品,一共有理科數(shù)學(xué).files/image438.gif) 種不同的選法.選出的3種商品中,沒有日用商品的選法有
種不同的選法.選出的3種商品中,沒有日用商品的選法有理科數(shù)學(xué).files/image440.gif) 種。所以選出的3種商品至少有一種日用商品的概率為
種。所以選出的3種商品至少有一種日用商品的概率為理科數(shù)學(xué).files/image442.gif) .
.
(2)假設(shè)商場將中獎獎金數(shù)額定為理科數(shù)學(xué).files/image039.gif) 元,則顧客在三歡抽獎中所獲得的獎金總額是一個(gè)隨機(jī)變量
元,則顧客在三歡抽獎中所獲得的獎金總額是一個(gè)隨機(jī)變量理科數(shù)學(xué).files/image445.gif) ,其所有可能的取值為
,其所有可能的取值為理科數(shù)學(xué).files/image447.gif)
理科數(shù)學(xué).files/image449.gif)
理科數(shù)學(xué).files/image451.gif)
理科數(shù)學(xué).files/image453.gif)
理科數(shù)學(xué).files/image455.gif)
于是顧客在三次抽獎中所獲得的獎金總額的期望值是
理科數(shù)學(xué).files/image457.gif) .
.
要使促銷方案對商場有利,因此應(yīng)有理科數(shù)學(xué).files/image459.gif) ,
,理科數(shù)學(xué).files/image461.gif) .
.
故商場應(yīng)將中獎獎金數(shù)額最高定為120元.才能使促銷方案對自己有利.
19.(1)證明:理科數(shù)學(xué).files/image463.gif) .
.
連接理科數(shù)學(xué).files/image465.gif) .
.
理科數(shù)學(xué).files/image467.gif) ,又
,又理科數(shù)學(xué).files/image469.gif)
理科數(shù)學(xué).files/image471.gif)
即理科數(shù)學(xué).files/image473.gif)
理科數(shù)學(xué).files/image475.gif) 平面
平面理科數(shù)學(xué).files/image210.gif) .
.
(2)方法1 取理科數(shù)學(xué).files/image478.gif) 的中點(diǎn)
的中點(diǎn)理科數(shù)學(xué).files/image360.gif) ,
,理科數(shù)學(xué).files/image119.gif) 的中點(diǎn)
的中點(diǎn)理科數(shù)學(xué).files/image482.gif) ,
,理科數(shù)學(xué).files/image484.gif) 為
為理科數(shù)學(xué).files/image121.gif) 的中點(diǎn),
的中點(diǎn),理科數(shù)學(xué).files/image487.gif) 或其補(bǔ)角是
或其補(bǔ)角是理科數(shù)學(xué).files/image212.gif) 與
與理科數(shù)學(xué).files/image214.gif) 所成的角.
所成的角.
∴連接理科數(shù)學(xué).files/image491.gif) 是
是理科數(shù)學(xué).files/image493.gif) 斜邊
斜邊理科數(shù)學(xué).files/image119.gif) 上的中線,
上的中線,理科數(shù)學(xué).files/image496.gif) ,
,
理科數(shù)學(xué).files/image498.gif) .
.
在理科數(shù)學(xué).files/image500.gif) 中,由余弦定理得
中,由余弦定理得理科數(shù)學(xué).files/image502.gif) ,
,
∴直線理科數(shù)學(xué).files/image212.gif) 與
與理科數(shù)學(xué).files/image214.gif) 所成的角為
所成的角為理科數(shù)學(xué).files/image506.gif) .
.
(3)方法l
理科數(shù)學(xué).files/image508.gif) 平面
平面理科數(shù)學(xué).files/image510.gif) ,過
,過理科數(shù)學(xué).files/image201.gif) 作
作理科數(shù)學(xué).files/image513.gif) 于
于理科數(shù)學(xué).files/image515.gif) ,連接
,連接理科數(shù)學(xué).files/image517.gif) ,
,
理科數(shù)學(xué).files/image519.gif) 是
是理科數(shù)學(xué).files/image517.gif) 在平面
在平面理科數(shù)學(xué).files/image510.gif) 上的射影,由三垂線定理得
上的射影,由三垂線定理得理科數(shù)學(xué).files/image522.gif) .
.
理科數(shù)學(xué).files/image524.gif) 是二面角
是二面角理科數(shù)學(xué).files/image216.gif) 的平面角,
的平面角,
理科數(shù)學(xué).files/image527.gif) ,又
,又理科數(shù)學(xué).files/image529.gif) .
.
在理科數(shù)學(xué).files/image531.gif) 中,
中,理科數(shù)學(xué).files/image533.gif) ,
,理科數(shù)學(xué).files/image535.gif) .
.
∴二面角理科數(shù)學(xué).files/image216.gif) 為
為理科數(shù)學(xué).files/image538.gif) .
.
(2)方法2
建立空間直角坐標(biāo)系理科數(shù)學(xué).files/image540.gif) .
.
則理科數(shù)學(xué).files/image542.gif)
理科數(shù)學(xué).files/image544.gif)
理科數(shù)學(xué).files/image546.gif) .
.
理科數(shù)學(xué).files/image548.gif) .
.
∴直線理科數(shù)學(xué).files/image212.gif) 與
與理科數(shù)學(xué).files/image214.gif) 所成的角為
所成的角為理科數(shù)學(xué).files/image506.gif) .
.
(3)方法2
在坐標(biāo)系中,平面理科數(shù)學(xué).files/image510.gif) 的法向量
的法向量理科數(shù)學(xué).files/image554.gif) .
.
設(shè)平面理科數(shù)學(xué).files/image556.gif) 的法向量
的法向量理科數(shù)學(xué).files/image558.gif) ,則
,則理科數(shù)學(xué).files/image560.gif) ,
,
求得理科數(shù)學(xué).files/image562.gif) ,
,
∴二面角理科數(shù)學(xué).files/image216.gif) 為
為理科數(shù)學(xué).files/image565.gif) .
.
20.理科數(shù)學(xué).files/image567.gif) 是首項(xiàng)為
是首項(xiàng)為理科數(shù)學(xué).files/image237.gif) 、公比為
、公比為理科數(shù)學(xué).files/image237.gif) 的等比數(shù)列,
的等比數(shù)列,理科數(shù)學(xué).files/image571.gif)
理科數(shù)學(xué).files/image573.gif)
(1)當(dāng)理科數(shù)學(xué).files/image227.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image576.gif)
理科數(shù)學(xué).files/image578.gif)
理科數(shù)學(xué).files/image580.gif)
理科數(shù)學(xué).files/image582.gif)
兩式相減得理科數(shù)學(xué).files/image584.gif)
理科數(shù)學(xué).files/image586.gif)
理科數(shù)學(xué).files/image588.gif) .
.
(2)理科數(shù)學(xué).files/image590.gif)
當(dāng)理科數(shù)學(xué).files/image592.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image594.gif) ,
,理科數(shù)學(xué).files/image596.gif) ,對
,對理科數(shù)學(xué).files/image235.gif) ,
,理科數(shù)學(xué).files/image599.gif) ,而
,而理科數(shù)學(xué).files/image592.gif) ,
,
理科數(shù)學(xué).files/image602.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image604.gif) 成立,即
成立,即理科數(shù)學(xué).files/image233.gif) .
.
當(dāng)理科數(shù)學(xué).files/image607.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image609.gif) .
.
理科數(shù)學(xué).files/image611.gif) 對
對理科數(shù)學(xué).files/image235.gif) 遞增,
遞增,理科數(shù)學(xué).files/image614.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image616.gif)
理科數(shù)學(xué).files/image618.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image620.gif) 對
對理科數(shù)學(xué).files/image235.gif) 成立,即
成立,即理科數(shù)學(xué).files/image233.gif) ,
,
綜上得,理科數(shù)學(xué).files/image237.gif) 的取值范圍是
的取值范圍是理科數(shù)學(xué).files/image625.gif) .
.
21.(1)設(shè)理科數(shù)學(xué).files/image627.gif) .
.
由拋物線定義,理科數(shù)學(xué).files/image629.gif) ,
,
理科數(shù)學(xué).files/image631.gif) .
.
理科數(shù)學(xué).files/image633.gif) 在
在理科數(shù)學(xué).files/image161.gif) 上,
上,理科數(shù)學(xué).files/image636.gif) ,又
,又理科數(shù)學(xué).files/image638.gif)
理科數(shù)學(xué).files/image640.gif)
理科數(shù)學(xué).files/image642.gif) 或
或理科數(shù)學(xué).files/image644.gif) 舍去.
舍去.
理科數(shù)學(xué).files/image646.gif)
∴橢圓理科數(shù)學(xué).files/image161.gif) 的方程為
的方程為理科數(shù)學(xué).files/image649.gif) .
.
(2)∵直線理科數(shù)學(xué).files/image121.gif) 的方程為
的方程為理科數(shù)學(xué).files/image652.gif) 為菱形,
為菱形,
理科數(shù)學(xué).files/image654.gif) ,設(shè)直線
,設(shè)直線理科數(shù)學(xué).files/image119.gif) 的方程為
的方程為理科數(shù)學(xué).files/image657.gif)
理科數(shù)學(xué).files/image659.gif) 、
、理科數(shù)學(xué).files/image661.gif) 在橢圓
在橢圓理科數(shù)學(xué).files/image161.gif) 上,
上,
理科數(shù)學(xué).files/image664.gif) .
.
設(shè)理科數(shù)學(xué).files/image666.gif) ,則
,則理科數(shù)學(xué).files/image668.gif) .
.
理科數(shù)學(xué).files/image670.gif) .
.
理科數(shù)學(xué).files/image672.gif) 的中點(diǎn)坐標(biāo)為
的中點(diǎn)坐標(biāo)為理科數(shù)學(xué).files/image674.gif) ,由
,由理科數(shù)學(xué).files/image065.gif) 為菱形可知,點(diǎn)
為菱形可知,點(diǎn)理科數(shù)學(xué).files/image674.gif) 在直線
在直線理科數(shù)學(xué).files/image677.gif) 上,
上,
理科數(shù)學(xué).files/image679.gif)
理科數(shù)學(xué).files/image681.gif)
∴直線理科數(shù)學(xué).files/image119.gif) 的方程為
的方程為理科數(shù)學(xué).files/image684.gif) ,即
,即理科數(shù)學(xué).files/image686.gif) .
.
22.(1)理科數(shù)學(xué).files/image688.gif) ,切線
,切線理科數(shù)學(xué).files/image266.gif) 的議程為
的議程為理科數(shù)學(xué).files/image691.gif) ,即
,即理科數(shù)學(xué).files/image693.gif) .
.
令理科數(shù)學(xué).files/image695.gif) 得
得理科數(shù)學(xué).files/image697.gif) ,令
,令理科數(shù)學(xué).files/image699.gif) 得
得理科數(shù)學(xué).files/image701.gif) ,
,
理科數(shù)學(xué).files/image703.gif) ,
,
理科數(shù)學(xué).files/image705.gif) .
.
理科數(shù)學(xué).files/image707.gif)
(2)由理科數(shù)學(xué).files/image709.gif) 及
及理科數(shù)學(xué).files/image711.gif) 得
得理科數(shù)學(xué).files/image713.gif) ,即
,即理科數(shù)學(xué).files/image715.gif) .
.
于是理科數(shù)學(xué).files/image717.gif)
當(dāng)且僅當(dāng)理科數(shù)學(xué).files/image719.gif) ,即
,即理科數(shù)學(xué).files/image721.gif) 時(shí),等號成立.
時(shí),等號成立.
理科數(shù)學(xué).files/image723.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image725.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image727.gif) .
.
(3)理科數(shù)學(xué).files/image729.gif)
由理科數(shù)學(xué).files/image731.gif) 得
得理科數(shù)學(xué).files/image733.gif)
當(dāng)理科數(shù)學(xué).files/image735.gif) ,即
,即理科數(shù)學(xué).files/image737.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image739.gif) ,
,
當(dāng)理科數(shù)學(xué).files/image741.gif) ,即
,即理科數(shù)學(xué).files/image743.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image745.gif)
理科數(shù)學(xué).files/image747.gif) 時(shí),
時(shí),理科數(shù)學(xué).files/image282.gif) 取得最小值,最小值為
取得最小值,最小值為理科數(shù)學(xué).files/image750.gif) .
.
由理科數(shù)學(xué).files/image752.gif) ,得
,得理科數(shù)學(xué).files/image754.gif) ,此時(shí),
,此時(shí),理科數(shù)學(xué).files/image282.gif) 最小值為
最小值為理科數(shù)學(xué).files/image757.gif) .
.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com