題目列表(包括答案和解析)
（12分）已知函數
，若
在區間[-2，2]上的最大值為20.
（1）求它在該區間上的最小值.
（2）當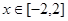
時，
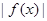≤m，（m>0）恒成立.求m的取值范圍.
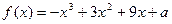，若
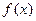在區間[-2，2]上的最大值為20.
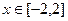時，
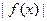≤m，（m>0）恒成立.求m的取值范圍.⒘已知函數
⑴求
的單調減區間；
⑵若在區間
上的最大值為20，求它在該區間上的最小值。
已知函數
⑴求
的單調減區間；
⑵若在區間
上的最大值為20，求它在該區間上的最小值。
（12分） 已知
。
（１）求
的單調區間。
（２）若在
上的最大值為20，求它在該區間上的最小值。
又在三角形PAC中,E,O分別為PC,AC的中點,
PA//EO.
平面EFOG，PA
平面EFOG，
PA//平面EFOG，即PA//平面EFG． ………………
…………………………6分
方法二：連AC,BD交于O點,連GO,FO,EO．
∵E,F分別為PC,PD的中點,∴
//
,
同理
//
又
//AB,
//
.
平面EFG//平面PAB.
又PA平面PAB,
平面EFG．…………………………………………6分
（2）取AD的中點H，連結GH，則由
知平面EFG即為平面EFHG。
∴
的單調減區間為
和
，單調增區間為
. …………4分
（2）設
，則
.
∴3
=
―3，2
=6，
=9，即= ―1，=3，=9.
故
.
………………………………………………8分
由⑴ 知在
上單調遞減,在
上單調遞增.
又
＞
=2+
，
∴
.
所以在
上的最小值為
. ………………………………12分
20．解:（1）由題意知
解得
，從而
.
21.解:（1）由已知可得
, ∴P是MN的中點，有
+
=1.
從而
+
=
+
=
=
為定值. ………………………………………4分
（2）由⑴ 知當+=1時，+=
+
=1.
+
+…+
,
①
又
+…+ 
,
②
① + ② 得
，故
.…………………………………8分
（3）當
≥2時，
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com