題目列表(包括答案和解析)
有一容量為10的樣本：2，4，7，6，5，9，7，10，3，8，則數據落在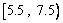
內的頻率為
A、0．3 B、0．4 C、0．35 D、0．25
容量為
的樣本數據，依次分為
組，如下表：
| 組號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 頻數 | 10 | 13 |  |  | 15 | 13 | 12 | 9 |
| A．0.28 | B．0.12 | C．0.15 | D．0.21 |
| 男 | 女 | 總計 | |
| 走天橋 | 40 | 20 | 60 |
| 走斑馬線 | 20 | 30 | 50 |
| 總計 | 60 | 50 | 110 |
| P（K2≥k） | 0.05 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 110×(40×30-20×20) |
| 60×50×60×50 |
將容量為100的樣本數據，按從小到大的順序分為5個組，如下表
| 組號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 頻數 | 10 | 13 | 14 | 14 | 15 | 13 | 12 | 9 |
則第三組的頻率是（ ）
A．0.14 B． 
C．0.03 D．
容量100為的樣本數據，按從小到大的順序分為8組，如下表：
|
組號 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
頻數 |
10 |
13 |
x |
14 |
15 |
13 |
12 |
9 |
第三組的頻數和頻率分別是 ( )
A．14和0.14 B．0.14和14 C．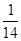 
和0.14
D． 
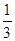和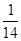
一、ABCBD BCABD
二、11.2 12. 
13.4 14.10 15. ①②③
三、16. 解：（1）
，
3分
由已知
，得
．
6分
（2）由（1）得
，
8分
當
時，
的最小值為
，
10分
由，得
值的集合為
． 13分
17. 解：（I）取AB的中點O，連接OP，OC 
PA=PB PO
AB
又在
中，
，
在
中，
，又
，故有
又
， 
面ABC 4分
又 PO
面PAB，面PAB面ABC
6分
（Ⅱ）以O為坐標原點，
分別以OB，OC，OP為軸，
軸，
軸建立坐標系，
如圖，則A
8分
設平面PAC的一個法向量為
。
得
令
，則
11分
設直線PB與平面PAC所成角為
，
于是
13分
18. 解：（1）
；
4分
（2）消費總額為1500元的概率是：
5分
消費總額為1400元的概率是：
6分
消費總額為1300元的概率是：
＝
，
所以消費總額大于或等于1300元的概率是
；
8分
（3）
，
，
＝
。所以
的分布列為：
0
1
2
3
0.294
0.448
0.222
0.036
數學期望是：
。 13分
19. 解：∵
的右焦點
∴橢圓的半焦距
，又
，
∴橢圓的
， 
.橢圓方程為
.
（Ⅰ）當
時，故橢圓方程為
， 3分
（Ⅱ）依題意設直線
的方程為：
，
聯立
得點
的坐標為
. 4分
將代入
得
.
設
、
，由韋達定理得
，
. 5分
又
，
.
7分
有實根， ∴點可以在圓上. 8分
（Ⅲ）假設存在滿足條件的實數
，
由
解得：
. 10分
∴
，
，又
.即
的邊長分別是
、
、
.
時，能使的邊長是連續的自然數。 1
3分
20. 解：（1）
．
1分
當
時，
，在
上單調遞增；
2分
當
，
時，
，在
上單調遞減；
時，，在
上單調遞增．
3分
綜上所述，當時，的單調遞增區間為；當時，的單調遞增區間為，單調遞減區間為．
4分
（2）充分性：
時，由（1）知，在x=1處有極小值也是最小值，
即
。而在
上單調遞減，在
上單調遞增，
所以在上有唯一的一個零點x=1． 6分
必要性：若函數f(x)存在唯一零點，即方程=0在上有唯一解，
因, 由（1）知，在
處有極小值也是最小值f(a)，
f(a)=0,即
．
7分
令
， 
．
當
時，
，
在上單調遞增；當
時，
，
在上單調遞減。
，=0只有唯一解．
因此=0在上有唯一解時必有．
綜上：在時， =0在上有唯一解的充要條件是． 9分
（3）證明：∵1<x<2, ∴
.
令
，∴
，11分
由（1）知，當時，，∴
，
∴
．∴
，
12分
∴F（x）在（1，2）上單調遞增，∴
，
∴
。∴
．
14分
21. （Ⅰ）解：考慮在矩陣
作用下，求出變換后的三角形的頂點坐標，從而求得三角形的面積，可先求得
，由
＝，得點
在矩陣
作用下變換所得到的點
，同理求得
在矩陣作用下變換所得到的點分別是
，
，計算得△
的面積為3．
7分
（Ⅱ）解：直線
的極坐標方程
，則
，
即
，所以直線的直角坐標方程為
； 2分
設
，其中
，則P到直線的距離
，其中
，∴ 當
時，
的最大值為
；當
時，的最小值為
。
7分
（Ⅲ）解：由柯西不等式，得
， 2分
即
．由條件，得
．解得
， 2分
當且僅當
時等號成立．代入
時，
；
時，
．所以，
的取值范圍是
．
7分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com