
題目列表(包括答案和解析)
設函數
(1)當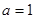 時,求曲線
時,求曲線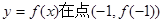 處的切線方程;
處的切線方程;
(2)當 時,求
時,求 的極大值和極小值;
的極大值和極小值;
(3)若函數 在區(qū)間
在區(qū)間 上是增函數,求實數
上是增函數,求實數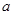 的取值范圍.
的取值范圍.
【解析】(1)中,先利用 ,表示出點
,表示出點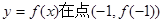 的斜率值
的斜率值 這樣可以得到切線方程。(2)中,當
這樣可以得到切線方程。(2)中,當 ,再令
,再令 ,利用導數的正負確定單調性,進而得到極值。(3)中,利用函數在給定區(qū)間遞增,說明了
,利用導數的正負確定單調性,進而得到極值。(3)中,利用函數在給定區(qū)間遞增,說明了 在區(qū)間
在區(qū)間 導數恒大于等于零,分離參數求解范圍的思想。
導數恒大于等于零,分離參數求解范圍的思想。
解:(1)當 ……2分
……2分
 ∴
∴
即 為所求切線方程。………………4分
為所求切線方程。………………4分
(2)當
令 ………………6分
………………6分
∴ 遞減,在(3,+
遞減,在(3,+ )遞增
)遞增
∴ 的極大值為
的極大值為 …………8分
…………8分
(3)
①若 上單調遞增。∴滿足要求。…10分
上單調遞增。∴滿足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 時,不合題意。綜上所述,實數
時,不合題意。綜上所述,實數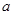 的取值范圍是
的取值范圍是
已知函數
(1)若函數 的圖象經過P(3,4)點,求a的值;
的圖象經過P(3,4)點,求a的值;
(2)比較 大小,并寫出比較過程;
大小,并寫出比較過程;
(3)若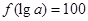 ,求a的值.
,求a的值.
【解析】本試題主要考查了指數函數的性質的運用。第一問中,因為函數 的圖象經過P(3,4)點,所以
的圖象經過P(3,4)點,所以 ,解得
,解得 ,因為
,因為 ,所以
,所以 .
.
(2)問中,對底數a進行分類討論,利用單調性求解得到。
(3)中,由 知,
知, .,指對數互化得到
.,指對數互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函數 的圖象經過
的圖象經過 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵當 時,
時, ;
;
當 時,
時, . ……………… 6分
. ……………… 6分
因為, ,
,
當 時,
時, 在
在 上為增函數,∵
上為增函數,∵ ,∴
,∴ .
.
即 .當
.當 時,
時, 在
在 上為減函數,
上為減函數,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
(本小題10分)已知函數 =
=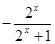 .
.
(1)用定義證明函數 在(-∞,+∞)上為減函數;
在(-∞,+∞)上為減函數;
(2)若x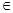 [1,2],求函數
[1,2],求函數 的值域;
的值域;
(3)若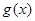 =
=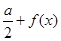 ,且當x
,且當x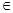 [1,2]時
[1,2]時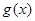
 恒成立,求實數
恒成立,求實數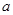 的取值范圍.
的取值范圍.
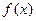 =
=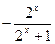 .
.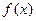 在(-∞,+∞)上為減函數;
在(-∞,+∞)上為減函數;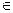 [1,2],求函數
[1,2],求函數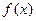 的值域;
的值域;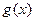 =
=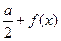 ,且當
,且當 x
x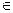 [1,2]時
[1,2]時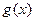
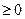 恒成立,求實數
恒成立,求實數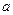 的取值范圍.
的取值范圍.(本小題滿分12分)探究函數 的最小值,并確定取得最小值時x的值.列表如下:
的最小值,并確定取得最小值時x的值.列表如下:
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
16 |
10 |
8.34 |
8.1 |
8.01 |
8 |
8.01 |
8.04 |
8.08 |
8.6 |
10 |
11.6 |
15.14 |
… |
請觀察表中y值隨x值變化的特點,完成以下的問題.
(1)函數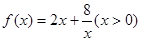 在區(qū)間(0,2)上遞減;函數
在區(qū)間(0,2)上遞減;函數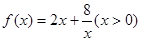 在區(qū)間 上遞增.當
在區(qū)間 上遞增.當 時,
時, .
.
(2)證明:函數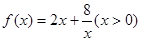 在區(qū)間(0,2)遞減.
在區(qū)間(0,2)遞減.
(3)思考:函數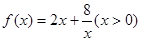 時,有最值嗎?是最大值還是最小值?此時x為何值?(直接回答結果,不需證明)
時,有最值嗎?是最大值還是最小值?此時x為何值?(直接回答結果,不需證明)
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com