
題目列表(包括答案和解析)
已知數列 是首項為
是首項為 的等比數列,且滿足
的等比數列,且滿足
 .
.
(1) 求常數 的值和數列
的值和數列 的通項公式;
的通項公式;
(2) 若抽去數列 中的第一項、第四項、第七項、……、第
中的第一項、第四項、第七項、……、第 項、……,余下的項按原來的順序組成一個新的數列
項、……,余下的項按原來的順序組成一個新的數列 ,試寫出數列
,試寫出數列 的通項公式;
的通項公式;
(3) 在(2)的條件下,設數列 的前
的前 項和為
項和為 .是否存在正整數
.是否存在正整數 ,使得
,使得 ?若存在,試求所有滿足條件的正整數
?若存在,試求所有滿足條件的正整數 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【解析】第一問中解:由 得
得 ,,
,,
又因為存在常數p使得數列 為等比數列,
為等比數列,
則 即
即 ,所以p=1
,所以p=1
故數列 為首項是2,公比為2的等比數列,即
為首項是2,公比為2的等比數列,即 .
.
此時 也滿足,則所求常數
也滿足,則所求常數 的值為1且
的值為1且
第二問中,解:由等比數列的性質得:
(i)當 時,
時, ;
;
(ii) 當 時,
時, ,
,
所以
第三問假設存在正整數n滿足條件,則 ,
,
則(i)當 時,
時,
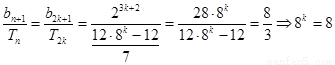
 ,
,
求曲線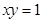 及直線
及直線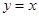 ,
,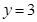 所圍成的平面圖形的面積.
所圍成的平面圖形的面積.
【解析】本試題主要是考查了定積分的運用。
解:做出曲線xy=1及直線y=x,y=3的草圖,則所求面積為陰影部分的面積
解方程組 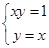 得直線y=x與曲線xy=1的交點坐標為(1,1)
得直線y=x與曲線xy=1的交點坐標為(1,1)
同理得:直線y=x與曲線y=3的交點坐標為(3,3)
直線y=3與曲線xy=1的交點坐標為(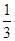 ,3)………………3分
,3)………………3分
因此,所求圖形的面積為
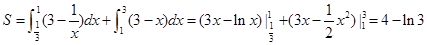
求由拋物線 與直線
與直線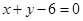 及
及 所圍成圖形的面積.
所圍成圖形的面積.
【解析】首先利用已知函數和拋物線作圖,然后確定交點坐標,然后利用定積分表示出面積為 ,所以得到
,所以得到 ,由此得到結論為
,由此得到結論為
解:設所求圖形面積為 ,則
,則

 =
= .即所求圖形面積為
.即所求圖形面積為 .
.


 已知△OFQ的面積為2
已知△OFQ的面積為2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com