
�}Ŀ�б�(�����𰸺ͽ���)
��(du��)���⺯��(sh��)f(x), x��D���ɰ��Dʾ��(g��u)��һ��(g��)��(sh��)�аl(f��)�������乤��ԭ������:
��ݔ�딵(sh��)��(j��)x0��D����(j��ng)��(sh��)�аl(f��)����ݔ��x1=f(x0)��
����x1![]() D���t��(sh��)�аl(f��)�����Y(ji��)����������x1��D���t��x1������ݔ��ˣ���ݔ��x2=f(x1)��������Ҏ(gu��)���^�m(x��)��ȥ.
D���t��(sh��)�аl(f��)�����Y(ji��)����������x1��D���t��x1������ݔ��ˣ���ݔ��x2=f(x1)��������Ҏ(gu��)���^�m(x��)��ȥ.
�F(xi��n)���x![]()
��1����ݔ��x0=![]() ���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)��{xn}��Ո(q��ng)��(xi��)��{xn}�������(xi��ng)��
���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)��{xn}��Ո(q��ng)��(xi��)��{xn}�������(xi��ng)��
��2����Ҫ��(sh��)�аl(f��)�����a(ch��n)��һ��(g��)�o(w��)�F�ij���(sh��)�У�ԇ��ݔ��ij�ʼ��(sh��)��(j��)x0��ֵ��
��3����ݔ��x0�r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)��{xn}���M�㌦(du��)����������(sh��)n����xn��xn+1����x0��ȡֵ����.
��(du��)���⺯��(sh��) ���ɰ����̈D��(g��u)��һ��(g��)��(sh��)�аl(f��)�������乤��ԭ�����£���ݔ�딵(sh��)��(j��)
���ɰ����̈D��(g��u)��һ��(g��)��(sh��)�аl(f��)�������乤��ԭ�����£���ݔ�딵(sh��)��(j��) ����(sh��)�аl(f��)����ݔ��
����(sh��)�аl(f��)����ݔ�� ������
������ ���t��(sh��)�аl(f��)�����Y(ji��)����������
���t��(sh��)�аl(f��)�����Y(ji��)���������� ���t��
���t�� ������ݔ�����ݔ��
������ݔ�����ݔ�� ,��������Ҏ(gu��)���^�m(x��)��ȥ.�F(xi��n)���x
,��������Ҏ(gu��)���^�m(x��)��ȥ.�F(xi��n)���x .
.
��1����ݔ�� ���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)��
���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)�� ��Ո(q��ng)��(xi��)����(sh��)��
��Ո(q��ng)��(xi��)����(sh��)�� �������(xi��ng)��
�������(xi��ng)��
��2����Ҫ��(sh��)�аl(f��)�����a(ch��n)��һ��(g��)�o(w��)�F�ij���(sh��)��(sh��)�У�ԇ��ݔ��ij�ʼ��(sh��)��(j��) ��ֵ��
��ֵ��
��3����ݔ�� �r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)��
�r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)�� �M�㣺��(du��)����������(sh��)
�M�㣺��(du��)����������(sh��) ������
������ ����
���� ��
��
ȡֵ����.
 ���ɰ����̈D��(g��u)��һ��(g��)��(sh��)�аl(f��)�������乤��ԭ�����£���ݔ�딵(sh��)��(j��)
���ɰ����̈D��(g��u)��һ��(g��)��(sh��)�аl(f��)�������乤��ԭ�����£���ݔ�딵(sh��)��(j��) ����(sh��)�аl(f��)����ݔ��
����(sh��)�аl(f��)����ݔ�� ������
������ ���t��(sh��)�аl(f��)�����Y(ji��)����������
���t��(sh��)�аl(f��)�����Y(ji��)���������� ���t��
���t�� ������ݔ�����ݔ��
������ݔ�����ݔ�� ,��������Ҏ(gu��)���^�m(x��)��ȥ.�F(xi��n)���x
,��������Ҏ(gu��)���^�m(x��)��ȥ.�F(xi��n)���x .
. ���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)��
���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)�� ��Ո(q��ng)��(xi��)����(sh��)��
��Ո(q��ng)��(xi��)����(sh��)�� �������(xi��ng)��
�������(xi��ng)�� ��ֵ��
��ֵ�� �r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)��
�r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)�� �M�㣺��(du��)����������(sh��)
�M�㣺��(du��)����������(sh��) ������
������ ����
���� ��
��
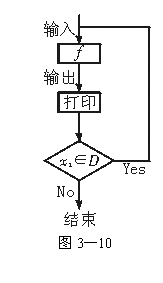 ��ݔ�딵(sh��)��(j��)x����D����(j��ng)��(sh��)�аl(f��)����ݔ��x1��f(x��)��
��ݔ�딵(sh��)��(j��)x����D����(j��ng)��(sh��)�аl(f��)����ݔ��x1��f(x��)��
����x1![]() D���t��(sh��)�аl(f��)�����Y(ji��)����������x1��D���t��x1������ݔ��ˣ���ݔ��x2��f(x1����������Ҏ(gu��)���^�m(x��)��ȥ��
D���t��(sh��)�аl(f��)�����Y(ji��)����������x1��D���t��x1������ݔ��ˣ���ݔ��x2��f(x1����������Ҏ(gu��)���^�m(x��)��ȥ��
�F(xi��n)���xf(x)��![]() ��
��
������ݔ��x����![]() ���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)�У�xn����Ո(q��ng)��(xi��)����(sh��)�У�xn���������(xi��ng)��
���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)�У�xn����Ո(q��ng)��(xi��)����(sh��)�У�xn���������(xi��ng)��
(��)��Ҫ��(sh��)�аl(f��)�����a(ch��n)��һ��(g��)�o(w��)�F�ij���(sh��)�У�ԇ��ݔ��ij�ʼ��(sh��)��(j��)x����ֵ��
(��)(��)��ݔ��x���r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)�У�xn���M�㣺��(du��)����������(sh��)n������xn��xn��������x����ȡֵ������
��(du��)���⺯��(sh��)f(x)��x��D���ɰ��Dʾ��(g��u)��һ��(g��)��(sh��)�аl(f��)�������乤��ԭ�����£�
(1)ݔ�딵(sh��)��(j��)x0��D����(j��ng)��(sh��)�аl(f��)����ݔ��x1��f(x0)��
(2)��x1![]() D���t��(sh��)�аl(f��)�����Y(ji��)����������x1��D���t��x1����ݔ��ˣ���ݔ��x2��f(x1)����
D���t��(sh��)�аl(f��)�����Y(ji��)����������x1��D���t��x1����ݔ��ˣ���ݔ��x2��f(x1)����
����Ҏ(gu��)���^�m(x��)��ȥ���F(xi��n)���xf(x)��![]() ��
��
(1)��ݔ��x0��![]() ���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)��{xn}��Ո(q��ng)��(xi��)����(sh��)��{xn}�������(xi��ng)��
���t�ɔ�(sh��)�аl(f��)�����a(ch��n)����(sh��)��{xn}��Ո(q��ng)��(xi��)����(sh��)��{xn}�������(xi��ng)��
(2)��Ҫ��(sh��)�аl(f��)�����a(ch��n)��һ��(g��)�o(w��)�F�ij���(sh��)�У�ԇ��ݔ��ij�ʼ��(sh��)��(j��)x0��ֵ��
(3)��ݔ��x0�r(sh��)���a(ch��n)���ğo(w��)�F��(sh��)��{xn}�M�㣺��(du��)��һ������(sh��)n������xn��xn+1����x0��ȡֵ������

1��B 2��C 3��B 4��C 5��B 6��B 7��C 8��B 9��C 10��B
11��C 12��D
��������
3����(d��ng)�W(xu��).files/image290.gif) �r(sh��)������(sh��)
�r(sh��)������(sh��)�W(xu��).files/image026.gif) ��
���W(xu��).files/image028.gif) �ϣ�
�ϣ��W(xu��).files/image030.gif) �������
��������W(xu��).files/image295.gif) ��
���W(xu��).files/image028.gif) �Ϻ�������ɵ�
�Ϻ�������ɵ��W(xu��).files/image298.gif)
��(d��ng)�W(xu��).files/image300.gif) �r(sh��)������(sh��)
�r(sh��)������(sh��)�W(xu��).files/image026.gif) ��
���W(xu��).files/image028.gif) �ϣ�
�ϣ��W(xu��).files/image030.gif) �����
�����
���W(xu��).files/image305.gif) ��
���W(xu��).files/image028.gif) �Ϻ����
�Ϻ����
�ɵ��W(xu��).files/image308.gif) ����(du��)������
����(du��)�������W(xu��).files/image310.gif) �����
�����
�����W(xu��).files/image312.gif) ���C�ϵ�
���C�ϵ��W(xu��).files/image314.gif) ��
��
4���ⷨһ��(li��n)���W(xu��).files/image316.gif) ����
�����W(xu��).files/image318.gif) ��
��
�W(xu��).files/image320.gif) ���̿��н⣬��
���̿��н⣬���W(xu��).files/image322.gif) �����
�����
���W(xu��).files/image324.gif) ���������
����������W(xu��).files/image326.gif) �����
�����
�W(xu��).files/image328.gif) ����
�����W(xu��).files/image330.gif)
�W(xu��).files/image332.gif) ��ȡֵ������
��ȡֵ�������W(xu��).files/image334.gif) ��
��
�ⷨ������(sh��)�νY(ji��)�ϣ���?y��n)�ֱ���W(xu��).files/image040.gif) ���^(gu��)���c(di��n)��0��1����Ҫʹֱ���c�E�A
���^(gu��)���c(di��n)��0��1����Ҫʹֱ���c�E�A�W(xu��).files/image042.gif) ���н��c(di��n)��(d��ng)�ՃH��(d��ng)�c(di��n)��0��1���ڙE�A�ϻ�E�A��(n��i)����
���н��c(di��n)��(d��ng)�ՃH��(d��ng)�c(di��n)��0��1���ڙE�A�ϻ�E�A��(n��i)�����W(xu��).files/image338.gif)
�W(xu��).files/image340.gif) ��
���W(xu��).files/image330.gif)
�W(xu��).files/image332.gif) ��ȡֵ������
��ȡֵ�������W(xu��).files/image334.gif) ��
��
5���W(xu��).files/image345.gif)
7��չ�_(k��i)ʽǰ���(xi��ng)��ϵ��(sh��)�M���W(xu��).files/image347.gif) �ɽ��
�ɽ���W(xu��).files/image349.gif) ����
�����W(xu��).files/image351.gif) ����ȥ�����Ķ���֪�����(xi��ng)��
����ȥ�����Ķ���֪�����(xi��ng)���W(xu��).files/image353.gif) ����C���_��
����C���_��
8���W(xu��).files/image355.gif) ����ʹ
����ʹ�W(xu��).files/image012.gif) ���溯��(sh��)���ʹ
���溯��(sh��)���ʹ�W(xu��).files/image358.gif) ���^���֪��
���^���֪���W(xu��).files/image149.gif) ��
���W(xu��).files/image153.gif) ������Ҫ����
������Ҫ�����W(xu��).files/image362.gif) ���t
���t�W(xu��).files/image364.gif)
�W(xu��).files/image366.gif) ������
�������W(xu��).files/image070.gif) ���ǜp����(sh��)����B���_
���ǜp����(sh��)����B���_
��(d��ng)�W(xu��).files/image369.gif) �r(sh��)��
�r(sh��)���W(xu��).files/image371.gif) ������
�������W(xu��).files/image070.gif) ����������(sh��)��������Ҫ��
����������(sh��)��������Ҫ��
9���W(xu��).files/image082.gif) �ȃr(ji��)��
�ȃr(ji��)��
�W(xu��).files/image375.gif)
��(hu��)�D��֪�W(xu��).files/image377.gif) ����
�����W(xu��).files/image379.gif) ��
��
10����D����ʾ���O(sh��)�W(xu��).files/image381.gif) ���c(di��n)
���c(di��n)�W(xu��).files/image104.gif) ��ֱ��
��ֱ���W(xu��).files/image091.gif) �ľ��x��
�ľ��x���W(xu��).files/image385.gif) ���t�ɒ��タ���x��
���t�ɒ��タ���x���W(xu��).files/image387.gif) ��
��
�W(xu��).files/image389.jpg)
�����c(di��n)�W(xu��).files/image104.gif) �ڙE�A�ϣ����E�A��һ���x��
�ڙE�A�ϣ����E�A��һ���x���W(xu��).files/image392.gif)
�əE�A�ڶ����x���W(xu��).files/image394.gif) ����֮��
����֮���W(xu��).files/image396.gif) ��
��
11����52����������ȡ13���Ƶ�ȫ��ȡ�����W(xu��).files/image398.gif) ��ȱ��ijһ�N��ɫ��ȡ����
��ȱ��ijһ�N��ɫ��ȡ�����W(xu��).files/image400.gif) ��ȱ�كɷN��ɫ��ȡ����
��ȱ�كɷN��ɫ��ȡ�����W(xu��).files/image402.gif) ��ȱ�����N��ɫ��ȡ����
��ȱ�����N��ɫ��ȡ�����W(xu��).files/image404.gif) ������(j��)�ݳ�ԭ����֪�ķN��ɫ�Rȫ��ȡ����
������(j��)�ݳ�ԭ����֪�ķN��ɫ�Rȫ��ȡ�����W(xu��).files/image406.gif) ��
��
12���O(sh��)�W(xu��).files/image126.gif) ���c(di��n)��
���c(di��n)���W(xu��).files/image226.gif) ���B
���B�W(xu��).files/image410.gif) ������֪��
������֪���W(xu��).files/image412.gif) ƽ��
ƽ���W(xu��).files/image130.gif) ����
�����W(xu��).files/image415.gif) ����
�����W(xu��).files/image417.gif) �����L(zh��ng)�����c(di��n)
�����L(zh��ng)�����c(di��n)�W(xu��).files/image419.gif) ���B
���B�W(xu��).files/image421.gif) ���t
���t�W(xu��).files/image423.gif) �������O(sh��)
�������O(sh��)�W(xu��).files/image425.gif) ���t
���t�W(xu��).files/image427.gif) ����
�����W(xu��).files/image429.gif)
�п�����W(xu��).files/image431.gif) ���t
���t�W(xu��).files/image433.gif) ��
��
��������}
13���W(xu��).files/image435.gif) ��
��
��ʾ�������ÓQԪ����ԭ����ʽ���W(xu��).files/image437.gif) Ҳ�����Ô�(sh��)�νY(ji��)�Ϸ���
Ҳ�����Ô�(sh��)�νY(ji��)�Ϸ���
���W(xu��).files/image439.gif) ����ͬһ����(bi��o)ϵ��(n��i)�քe��(hu��)���@�ɂ�(g��)����(sh��)�ĈD���ɈDֱ�^�ý⼯��
����ͬһ����(bi��o)ϵ��(n��i)�քe��(hu��)���@�ɂ�(g��)����(sh��)�ĈD���ɈDֱ�^�ý⼯��
14��12�W(xu��).files/image441.gif) ����ʾ����(j��ng)�Д࣬
����ʾ����(j��ng)�Д࣬�W(xu��).files/image266.gif) �����F(tu��n)��ֱ����������֪�������İ돽��
�����F(tu��n)��ֱ����������֪�������İ돽���W(xu��).files/image060.gif) ��
��
15���W(xu��).files/image445.gif) ����ʾ������
����ʾ�������W(xu��).files/image447.gif) ��
���W(xu��).files/image449.gif)
����W(xu��).files/image451.gif) ����
�����W(xu��).files/image453.gif)
�W(xu��).files/image455.gif)
���ԣ���(d��ng)�W(xu��).files/image457.gif) �r(sh��)��
�r(sh��)���W(xu��).files/image459.gif) ȡ����Сֵ��
ȡ����Сֵ��
16���٢ڢ�
��������}
17��и���W(xu��).files/image461.gif)
�W(xu��).files/image463.gif) �������Ҷ����ã�
�������Ҷ����ã��W(xu��).files/image465.gif)
�W(xu��).files/image467.gif)
�W(xu��).files/image469.gif) ��
���W(xu��).files/image471.gif) ��
��
�W(xu��).files/image473.gif) ������(ji��n)��
������(ji��n)���W(xu��).files/image475.gif)
�W(xu��).files/image477.gif) ���߅�����Σ�
���߅�����Σ�
�f(shu��)�������}��������������Y(ji��)�ϵ��}Ŀ���ȿ����������Ļ���֪�R(sh��)���ֿ��������ǵ����P(gu��n)֪�R(sh��)�������ε��Π�ȿ��ɽǴ_����Ҳ����߅�_������˼ȿɏĽ����֣���߅����ǣ�Ҳ�ɏ�߅���֣��ѽǻ���߅��(l��i)�Д������ε��Π
18���⣺��1���ڵ�һ�θ��Q���ݹ����У�����Ҫ���Q���ݵĸ��ʞ��W(xu��).files/image479.gif) ��Ҫ���Q2ֻ���ݵĸ��ʞ�
��Ҫ���Q2ֻ���ݵĸ��ʞ��W(xu��).files/image481.gif) ��
��
��2����(du��)ԓ�K���(l��i)�f(shu��)���ڵ�1��2�ζ����Q�˟��ݵĸ��ʞ��W(xu��).files/image483.gif) ���ڵ�һ��δ���Q���ݶ��ڵڶ�����Ҫ���Q���ݵĸ��ʞ�
���ڵ�һ��δ���Q���ݶ��ڵڶ�����Ҫ���Q���ݵĸ��ʞ��W(xu��).files/image485.gif) ��������ĸ��ʞ�
��������ĸ��ʞ��W(xu��).files/image487.gif) ��
��
��3����(d��ng)�W(xu��).files/image207.gif) �r(sh��)��
�r(sh��)��
�ɣ�2��֪�ڶ��Ο��ݸ��Q�����У�ij�K�����Q�ĸ����W(xu��).files/image490.gif)
�����ٓQ4ֻ���ݵĸ��ʞ��W(xu��).files/image492.gif)
�W(xu��).files/image494.gif)
�W(xu��).files/image496.gif)
�W(xu��).files/image498.gif)
19���⣺�W(xu��).files/image500.gif) ]
]
��?y��n)麯�?sh��)�W(xu��).files/image012.gif) ��
���W(xu��).files/image503.gif) ̎���о�б�ʞ�
̎���о�б�ʞ��W(xu��).files/image087.gif)
�����W(xu��).files/image506.gif)
���W(xu��).files/image508.gif) ��
��
���W(xu��).files/image510.gif)
���W(xu��).files/image512.gif) ��
��
��1������(sh��)�W(xu��).files/image012.gif) ��
���W(xu��).files/image218.gif) �r(sh��)�ИOֵ
�r(sh��)�ИOֵ
�W(xu��).files/image516.gif) ��
��
��ʽ�٢ڢ۵��W(xu��).files/image518.gif)
�����W(xu��).files/image520.gif) ��
��
��2����?y��n)麯�?sh��)�W(xu��).files/image012.gif) �څ^(q��)�g
�څ^(q��)�g�W(xu��).files/image221.gif) �φ��{(di��o)�f�������Ԍ�(d��o)����(sh��)
�φ��{(di��o)�f�������Ԍ�(d��o)����(sh��)�W(xu��).files/image524.gif) �څ^(q��)�g
�څ^(q��)�g�W(xu��).files/image221.gif) ��ֵ����ڻ�����㣮
��ֵ����ڻ�����㣮
�t�W(xu��).files/image527.gif)
���W(xu��).files/image529.gif) �����Ԍ�(sh��)��(sh��)
�����Ԍ�(sh��)��(sh��)�W(xu��).files/image188.gif) ��ȡֵ������
��ȡֵ�������W(xu��).files/image532.gif) ��
��
20���⣺��1���B���W(xu��).files/image534.gif) ��?y��n)?sub>
��?y��n)?sub>�W(xu��).files/image230.gif) ƽ��
ƽ���W(xu��).files/image232.gif) ��ƽ��
��ƽ���W(xu��).files/image538.gif) ƽ��
ƽ���W(xu��).files/image540.gif)
�����W(xu��).files/image542.gif) ����
�����W(xu��).files/image242.gif) ��
���W(xu��).files/image239.gif) �����c(di��n)����
�����c(di��n)�����W(xu��).files/image226.gif) ��
���W(xu��).files/image228.gif) �����c(di��n)
�����c(di��n)
�W(xu��).files/image548.gif)
�W(xu��).files/image550.gif) ����
�����W(xu��).files/image120.gif)
�W(xu��).files/image553.gif) ��
���W(xu��).files/image236.gif) �c����
�c�����W(xu��).files/image120.gif) ���ɵĽ�
���ɵĽ�
���W(xu��).files/image557.gif) �У�
�У��W(xu��).files/image559.gif)
�W(xu��).files/image561.gif)
�W(xu��).files/image563.jpg) ����
�����W(xu��).files/image236.gif) �c����
�c�����W(xu��).files/image120.gif) ���ɵĽǞ�45�㣮
���ɵĽǞ�45�㣮
��2���ⷨһ����D����ֱ������(bi��o)ϵ�W(xu��).files/image567.gif)
�t�W(xu��).files/image569.gif) ��
�� �W(xu��).files/image571.gif)
�W(xu��).files/image573.gif) �O(sh��)
�O(sh��)�W(xu��).files/image244.gif) �c(di��n)������(bi��o)��
�c(di��n)������(bi��o)���W(xu��).files/image576.gif)
���W(xu��).files/image578.gif)
�W(xu��).files/image580.gif)
�W(xu��).files/image582.gif)
�W(xu��).files/image584.gif)
�W(xu��).files/image586.gif) �c(di��n)
�c(di��n)�W(xu��).files/image244.gif) ������(bi��o)��
������(bi��o)���W(xu��).files/image589.gif)
�W(xu��).files/image591.gif)
���W(xu��).files/image593.gif) ��
��
�ⷨ�����W(xu��).files/image595.gif) ƽ��
ƽ���W(xu��).files/image597.gif)
�W(xu��).files/image599.gif) ����
�����W(xu��).files/image248.gif)
�W(xu��).files/image602.gif) ƽ��
ƽ���W(xu��).files/image604.gif)
���������W(xu��).files/image597.gif) �У�
�У��W(xu��).files/image607.gif)
�W(xu��).files/image609.gif) ��
��
21���⣺��1���O(sh��)�c(di��n)�W(xu��).files/image149.gif) ��
���W(xu��).files/image151.gif) ������(bi��o)�քe��
������(bi��o)�քe���W(xu��).files/image613.gif) ��
���W(xu��).files/image615.gif) ���c(di��n)
���c(di��n)�W(xu��).files/image264.gif) ������(bi��o)��
������(bi��o)���W(xu��).files/image618.gif)
��(d��ng)�W(xu��).files/image620.gif) �r(sh��)���O(sh��)ֱ��
�r(sh��)���O(sh��)ֱ���W(xu��).files/image091.gif) ��б�ʞ�
��б�ʞ��W(xu��).files/image275.gif)
�W(xu��).files/image624.gif) ֱ��
ֱ���W(xu��).files/image091.gif) �^(gu��)�c(di��n)
�^(gu��)�c(di��n)�W(xu��).files/image256.gif)
�W(xu��).files/image628.gif) �ķ��̞�
�ķ��̞��W(xu��).files/image630.gif)
����֪�W(xu��).files/image632.gif) ��
��
�W(xu��).files/image634.gif) ��
��
�W(xu��).files/image636.gif) ��
��
�W(xu��).files/image638.gif) ��
��
��ʽ��һʽ�ڵ�
�W(xu��).files/image640.gif) ��
��
��ʽ+ʽ�ܵ�
�W(xu��).files/image642.gif) ��
��
����ʽ�ݡ�ʽ���W(xu��).files/image644.gif)
���c(di��n)�W(xu��).files/image264.gif) ������(bi��o)�M�㷽��
������(bi��o)�M�㷽��
�W(xu��).files/image647.gif) ��
��
��(d��ng)�W(xu��).files/image649.gif) �r(sh��)��
�r(sh��)���W(xu��).files/image275.gif) �����ڣ��˕r(sh��)
�����ڣ��˕r(sh��)�W(xu��).files/image091.gif) ƽ����
ƽ�����W(xu��).files/image653.gif) �S�����
�S������W(xu��).files/image266.gif) �����c(di��n)
�����c(di��n)�W(xu��).files/image264.gif) һ������
һ�������W(xu��).files/image657.gif) �S�ϣ���
�S�ϣ����W(xu��).files/image264.gif) ������(bi��o)��
������(bi��o)���W(xu��).files/image660.gif) ,�@Ȼ�c(di��n)
,�@Ȼ�c(di��n)�W(xu��).files/image264.gif) ��
���W(xu��).files/image032.gif) ��0���M�㷽�̢�
��0���M�㷽�̢�
�C�ϣ��c(di��n)�W(xu��).files/image264.gif) ������(bi��o)�M�㷽��
������(bi��o)�M�㷽���W(xu��).files/image647.gif)
�O(sh��)���̢�����ʾ���������W(xu��).files/image666.gif)
�t���W(xu��).files/image668.gif) ,
,
���W(xu��).files/image670.gif)
��?y��n)?sub>�W(xu��).files/image672.gif) ������֪
������֪�W(xu��).files/image258.gif) ��
��
���Ԯ�(d��ng)�W(xu��).files/image675.gif) �r(sh��)��
�r(sh��)���W(xu��).files/image677.gif) ������
�������W(xu��).files/image666.gif) �c�E�A
�c�E�A�W(xu��).files/image153.gif) ����ֻ��һ��(g��)���c(di��n)
����ֻ��һ��(g��)���c(di��n)�W(xu��).files/image256.gif) ��
��
��(d��ng)�W(xu��).files/image682.gif) �r(sh��)��
�r(sh��)���W(xu��).files/image684.gif) ������
�������W(xu��).files/image666.gif) �c�E�A
�c�E�A�W(xu��).files/image153.gif) �](m��i)�н��c(di��n)����?y��n)�?��0���ڙE�A��(n��i)����������
�](m��i)�н��c(di��n)����?y��n)�?��0���ڙE�A��(n��i)�����������W(xu��).files/image666.gif) �ϣ���������
�ϣ����������W(xu��).files/image666.gif) �ڙE�A��(n��i)�����c(di��n)
�ڙE�A��(n��i)�����c(di��n)�W(xu��).files/image264.gif) ��܉�E���̞�
��܉�E���̞��W(xu��).files/image690.gif)
�W(xu��).files/image692.gif)
��2�����W(xu��).files/image694.gif) �������
��������W(xu��).files/image666.gif) �c
�c�W(xu��).files/image653.gif) �S�����c(di��n)��0��0������0��
�S�����c(di��n)��0��0������0���W(xu��).files/image188.gif) ��
��
���W(xu��).files/image699.gif) �������
��������W(xu��).files/image666.gif) �c
�c�W(xu��).files/image657.gif) �S�����c(di��n)��0��0������
�S�����c(di��n)��0��0�������W(xu��).files/image032.gif) ��0��
��0��
��(d��ng)�W(xu��).files/image703.gif) �����c(di��n)
�����c(di��n)�W(xu��).files/image256.gif) ��ԭ�c(di��n)�r(sh��)����
��ԭ�c(di��n)�r(sh��)�����W(xu��).files/image032.gif) ��0������0��
��0������0���W(xu��).files/image188.gif) ���c��0��0���غϣ�����
���c��0��0���غϣ������W(xu��).files/image666.gif) �c����(bi��o)�Sֻ��һ��(g��)���c(di��n)��0��0����
�c����(bi��o)�Sֻ��һ��(g��)���c(di��n)��0��0����
��(d��ng)�W(xu��).files/image709.gif) ����
�����W(xu��).files/image711.gif) �����c(di��n)
�����c(di��n)�W(xu��).files/image256.gif) ���ڙE�A
���ڙE�A�W(xu��).files/image153.gif) �����ڳ�ȥԭ�c(di��n)��
�����ڳ�ȥԭ�c(di��n)���W(xu��).files/image653.gif) �S�ϕr(sh��)������
�S�ϕr(sh��)�������W(xu��).files/image666.gif) �c����(bi��o)�S�Ѓɂ�(g��)���c(di��n)��0��
�c����(bi��o)�S�Ѓɂ�(g��)���c(di��n)��0���W(xu��).files/image188.gif) ���c��0��0����ͬ������(d��ng)
���c��0��0����ͬ������(d��ng)
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com