
�}Ŀ�б�(�����𰸺ͽ���)
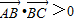 ���ǡ���ABC���g�������Ρ��ģ� ��
���ǡ���ABC���g�������Ρ��ģ� ��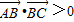 ���ǡ���ABC���g�������Ρ��ģ� ��
���ǡ���ABC���g�������Ρ��ģ� �� ���ǡ���ABC���g�������Ρ��ģ� ��
���ǡ���ABC���g�������Ρ��ģ� ��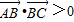 ���ǡ���ABC���g�������Ρ��ģ� ��
���ǡ���ABC���g�������Ρ��ģ� ��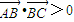 ���ǡ���ABC���g�������Ρ��ģ� ��
���ǡ���ABC���g�������Ρ��ģ� ��һ������}��ÿ�}5�֣����ƿ���55�֡��Ŀƿ���60�֣���
1. �ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image283.gif) �� 2. ����2���ģ�
�� 2. ����2���ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image285.gif) ��
3. ����1.885���ģ�2��
��
3. ����1.885���ģ�2��
4. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image287.gif) ���ģ�1.885�� 5. ����
���ģ�1.885�� 5. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image289.gif) ���ģ�4��
6. ����
���ģ�4��
6. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image291.gif) ���ģ�
���ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image287.gif) ��
��
7. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image293.gif) ���ģ�
���ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image289.gif) �� 8. ����
�� 8. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image130.gif) ���ģ�6�� 9. ����
���ģ�6�� 9. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image296.gif) ���ģ�
���ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image298.gif) ��
��
10. ����1�� �ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image130.gif) �� 11. ����
�� 11. �����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image300.gif) ���ģ�
���ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image296.gif) �� 12. �ģ�
�� 12. �ģ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image300.gif) ��
��
�����x���}��ÿ�}4�֣�����16�֣���
�}̖(h��o)
��12����13
��13����14
����14���ģ�15
��15���ģ�16
��
A
C
B
C
��������}��
16.�������M��12�֣�
�⣺��?y��n)钁�タ�Ľ��c(di��n)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image166.gif) ������(bi��o)��
������(bi��o)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image303.gif) ���O(sh��)
���O(sh��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image305.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image307.gif) ��
��
�ɗl�����tֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �ķ��̞�
�ķ��̞��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image310.gif) ��
��
���뒁�タ�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image164.gif) ���ɵ�
���ɵ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image312.gif) ���t
���t�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image314.gif) .
.
���ǣ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image316.gif) .
.
��2
��4
��8
��12
17.���ģ��M��12�֣�
�⣺��?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image318.gif) �������ɗl���ɵ�
�������ɗl���ɵ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image320.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image100.gif) .
.
����(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image114.gif) �ǹ���
�ǹ����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image323.gif) �ĵȱȔ�(sh��)��.
�ĵȱȔ�(sh��)��.
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image325.gif) ��
��
���ԣ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image327.gif) .
.
��4
��6
��8
��12
������17.���ģ�18. ���M��14�֣�
�⣺��?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image329.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image331.gif)
���ԣ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image333.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image335.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image337.gif)
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image339.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image341.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image343.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image345.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image347.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image343.gif)
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image183.gif) ����
����
��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image349.gif) �r(sh��)��
�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image351.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image353.gif) ����(d��ng)
����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image355.gif) �r(sh��)��
�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image357.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image359.gif) .
.
���ԣ������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image361.gif) .
.
��3
��7
��11
��14
18.(�����M��15�֣���1С�}6�֣���2С�}9�֣�
�⣺��1����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image363.gif) �r(sh��)��
�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image365.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image367.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image369.gif)
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image371.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image373.gif) ������
�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image375.gif) .
.
��2���C���ɔ�(sh��)�W(xu��)�w�{��
��i����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image377.gif) �r(sh��)����֪
�r(sh��)����֪�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image379.gif) �����攵(sh��)��
�����攵(sh��)��
��ii�����O(sh��)��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image381.gif) �r(sh��)��
�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image383.gif) ������
�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image385.gif) ���攵(sh��)��
���攵(sh��)��
�t��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image387.gif) �r(sh��)��
�r(sh��)��
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image389.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image391.gif)
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image393.gif) ����
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image395.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image397.gif) ������
�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image399.gif) ��ż��(sh��)��
��ż��(sh��)��
���ɚw�{���O(sh��)֪�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image385.gif) ���攵(sh��)����
���攵(sh��)�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image402.gif) Ҳ���攵(sh��).
Ҳ���攵(sh��).
�C�ϣ�i������ii����֪���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image404.gif) ��ֵһ�����攵(sh��).
��ֵһ�����攵(sh��).
�C��������?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image406.gif)
��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image408.gif) ���攵(sh��)�r(sh��)��
���攵(sh��)�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image410.gif)
�t��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image377.gif) �r(sh��)��
�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image379.gif) ���攵(sh��)����(d��ng)
���攵(sh��)����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image414.gif) �r(sh��)��
�r(sh��)��
��?y��n)����?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image416.gif) �б��ܱ�2���������Ԟ�ż��(sh��)��
�б��ܱ�2���������Ԟ�ż��(sh��)��
���ǣ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image410.gif) �؞��攵(sh��)��
�؞��攵(sh��)��
��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image408.gif) ��ż��(sh��)�r(sh��)��
��ż��(sh��)�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image419.gif)
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image421.gif) ���ܱ�2����������
���ܱ�2�����������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image404.gif) �؞��攵(sh��).
�؞��攵(sh��).
�C�Ͽ�֪���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image096.gif) ���(xi��ng)�����攵(sh��).
���(xi��ng)�����攵(sh��).
��3
��6
��8
��10
��14
��15
��10
��14
��15
19. ���ģ��M��14�֣�
�⣺��D���O(sh��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image270.gif) ���c(di��n)��
���c(di��n)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image425.gif) ��(li��n)�Y(ji��)
��(li��n)�Y(ji��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image428.gif) .
.
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image430.gif) ���}�⣬
���}�⣬�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image432.gif) ,
,�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image434.gif) ,����
,�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image436.gif) ���߅�����Σ�
���߅�����Σ�
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image438.gif) ����
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image440.gif) .
.
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image442.gif) ��
��
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image444.gif) .
.
���A�F�w�ĵ���A��e���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image446.gif) ,
,
���ԈA�F�w�w�e�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image448.gif) .
.
��3
��8
��10
��14
������19. ���ģ�20. ���M��16�֣���1С�}4�֣���2С�}6�֣���3С�}6�֣�
�⣺��1�����}�⣬��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image214.gif) ֮�g�ľ��x��
֮�g�ľ��x���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) ��(y��ng)λ��
��(y��ng)λ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image264.gif) �Ϸ���
�Ϸ���
�Ҵ˕r(sh��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image210.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) ߅�ϵĸߞ�
߅�ϵĸߞ�
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image454.gif) ����?y��n)?sub>
����?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image456.gif) �ף��ɵ�
�ף��ɵ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image458.gif) ��.
��.
���ԣ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image460.gif) ƽ���ף�
ƽ���ף�
������ͨ�L(f��ng)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image218.gif) ��ͨ�L(f��ng)��e��
��ͨ�L(f��ng)��e���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image463.gif) ƽ����.
ƽ����.
��2��1�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image465.gif) ��D��1����ʾ����(d��ng)
��D��1����ʾ����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) �ھ��΅^(q��)��(d��ng)����
�ھ��΅^(q��)��(d��ng)�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image467.gif) �r(sh��)��
�r(sh��)��
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image469.gif) ����e
����e�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image471.gif) ��
��
2�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image465.gif) ��D��2����ʾ����(d��ng)
��D��2����ʾ����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) �ڰ�A�΅^(q��)��(d��ng)����
�ڰ�A�΅^(q��)��(d��ng)�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image473.gif) �r(sh��)��
�r(sh��)��
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image474.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image476.gif) ���ʿɵ�
���ʿɵ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image469.gif) ����e
����e
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image478.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image480.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image482.gif) ��
��
�C�Ͽɵã�
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image484.gif)
��3��1�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image465.gif) ��(d��ng)
��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) �ھ��΅^(q��)��(d��ng)�r(sh��)��
�ھ��΅^(q��)��(d��ng)�r(sh��)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image012.gif) �څ^(q��)�g
�څ^(q��)�g�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image487.gif) �φ��{(di��o)�f�p��
�φ��{(di��o)�f�p��
�t���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image489.gif) ��
��
2�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image465.gif) ��(d��ng)
��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image212.gif) �ڰ�A�΅^(q��)��(d��ng)�r(sh��)��
�ڰ�A�΅^(q��)��(d��ng)�r(sh��)��
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image491.gif) ��
��
��̖(h��o)�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image493.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image495.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image473.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image493.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image498.gif) .
.
�����(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image500.gif) ���ף��r(sh��)��ÿ��(g��)����ͨ�L(f��ng)��
���ף��r(sh��)��ÿ��(g��)����ͨ�L(f��ng)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image218.gif) �õ����ͨ�L(f��ng)��e�������e��
�õ����ͨ�L(f��ng)��e�������e���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image503.gif) ��ƽ���ף�.
��ƽ���ף�.
��2
��4
��6
��9
��10
��12
��15
��16
21���ģ��M��18�֣���1С�}5�֣���2С�}6�֣���3С�}7�֣�
�⣺��1���O(sh��)�ҽ��c(di��n)����(bi��o)���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image505.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image507.gif) ��.
��.
��?y��n)��p����C����S�p������������u�����؞��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image509.gif) ��
��
�Ɍ�(du��)�Q�Կ�֪���ҽ��c(di��n)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image166.gif) ���ɗl�u�������x��ȣ���
���ɗl�u�������x��ȣ����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image512.gif) .
.
���ǿ�֪���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image514.gif) �����ֱ�������Σ��t��
�����ֱ�������Σ��t���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image516.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image518.gif) ��
��
���ɵ��S�p�����У��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image520.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image522.gif) .
.
�������S�p�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image249.gif) �ķ��̞�
�ķ��̞��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image525.gif) .
.
��2���O(sh��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image305.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image307.gif) ���p����
���p�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image249.gif) ֱ��
ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �ăɂ�(g��)���c(di��n).
�ăɂ�(g��)���c(di��n).
��?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image531.gif) ��ֱ��
��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �ķ���������
�ķ����������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image168.gif) ��ֱ��
��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �ķ��̞�
�ķ��̞�
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image533.gif) .
.
�����p�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image249.gif) �ķ���
�ķ����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image525.gif) ���ɵ�
���ɵ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image535.gif) ��
��
�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image537.gif)
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image539.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image541.gif) .
.
��3�����O(sh��)���ڶ��c(di��n)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image543.gif) ��ʹ
��ʹ�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image545.gif) �鳣��(sh��)������
�鳣��(sh��)�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image547.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image549.gif) ��ֱ��
��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �c�p����
�c�p�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image249.gif) �ăɂ�(g��)���c(di��n)������(bi��o).
�ăɂ�(g��)���c(di��n)������(bi��o).
�ٮ�(d��ng)ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image185.gif) �S����ֱ�r(sh��)���O(sh��)ֱ��
�S����ֱ�r(sh��)���O(sh��)ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �ķ��̞�
�ķ��̞��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image556.gif)
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image525.gif) ���ɵ�
���ɵ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image558.gif) .
.
���}���֪���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image560.gif) ���t��
���t���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image562.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image564.gif) ��
��
���ǣ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image566.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image568.gif)
�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image570.gif)
Ҫʹ�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image545.gif) ���c
���c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image572.gif) �o�P(gu��n)�ij���(sh��)����(d��ng)�҃H��(d��ng)
�o�P(gu��n)�ij���(sh��)����(d��ng)�҃H��(d��ng)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image574.gif) ���˕r(sh��)
���˕r(sh��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image576.gif) .
.
�ڮ�(d��ng)ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image170.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image185.gif) �S��ֱ�r(sh��)���ɵ��c(di��n)
�S��ֱ�r(sh��)���ɵ��c(di��n)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image579.gif) ,
,�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image581.gif) ��
��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image574.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image576.gif) ���鳣��(sh��).
���鳣��(sh��).
�C�Ͽ�֪�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image185.gif) �S�ϴ��ڶ��c(di��n)
�S�ϴ��ڶ��c(di��n)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image584.gif) ��ʹ
��ʹ�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image576.gif) �鳣��(sh��).
�鳣��(sh��).
��3
��5
��7
��9
��11
��13
��16
��17
��18
20�������M��22�֣���1С�}4�֣���2С�}6�֣���3С�}12�֣�
�⣺��1���ⷨһ�����}�⣬��߅���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image198.gif) ��ֱ�����Σ���
��ֱ�����Σ����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image270.gif) ��
��
�t�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image244.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ���ɵĽǼ���
���ɵĽǼ����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image588.gif) .
.
��?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image590.gif) ����
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image232.gif) ƽ��
ƽ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image198.gif) ��
��
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image592.gif) ƽ��
ƽ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image594.gif) ���t��
���t���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image596.gif) .
.
��?y��n)?sub>�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image598.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image438.gif) ,
,
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image601.gif) ���t
���t�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image603.gif) ��
��
������ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image244.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ���ɽǵĴ�С��
���ɽǵĴ�С���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image605.gif) .
.
�ⷨ������D�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image055.gif) ��ԭ�c(di��n)��ֱ��
��ԭ�c(di��n)��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image214.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image185.gif) �S��ֱ��
�S��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image611.gif) �S��ֱ��
�S��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image613.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image615.gif) �S��
�S��
�������gֱ������(bi��o)ϵ.
�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image617.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image619.gif) ���t��
���t���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image621.gif) ����
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image623.gif)
�t����ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image244.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ���ɽ�
���ɽ��ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image625.gif) �M��
�M���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image627.gif) ,
,
���ԣ�����ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image244.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ���ɽǵĴ�С��
���ɽǵĴ�С���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image605.gif) .
.
��2���ⷨһ���ɗl�����^�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image154.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image630.gif) �������
��������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image166.gif) ��(li��n)�Y(ji��)
��(li��n)�Y(ji��)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image633.gif) .
.
�������ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image635.gif) ����
�����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image253.gif) �c
�c�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ���ɽǼ���
���ɽǼ����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image637.gif) .
.
��ƽ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image198.gif) �У���
�У����ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image055.gif) ��ԭ�c(di��n)��ֱ��
��ԭ�c(di��n)��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image214.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image185.gif) �S��ֱ��
�S��ֱ���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image246.gif) ��
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image611.gif) �S������ƽ��ֱ������(bi��o)ϵ. �O(sh��)��(d��ng)�c(di��n)
�S������ƽ��ֱ������(bi��o)ϵ. �O(sh��)��(d��ng)�c(di��n)�ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image645.gif) ��
��
�t���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image647.gif)
���ڶ��W(xu��)�ڸ�����(sh��)�W(xu��)�|(zh��)���{(di��o)�У��������£�.files/image649.gif) ƽ��
ƽ��
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com