題目列表(包括答案和解析)
如圖，橢圓中心在原點，F為左焦點，當
⊥
時其離心率為
，此類橢圓被稱為“黃金橢圓”．
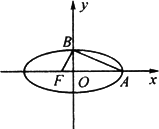
(1)類比“黃金橢圓”，可推算出“黃金雙曲線”的離心率等于多少？(只要寫出結論即可)
(2)已知橢圓E：
的一個焦點f(c，0)(c＞0)，試證：若a，b，c不是等比數列，則E一定不是“黃金橢圓”．
“肇實，正名芡實，因肇慶所產之芡實顆粒大、藥力強，故名．”某科研所為進一步改良肇實，為此對肇實的兩個品種(分別稱為品種A和品種B)進行試驗．選取兩大片水塘，每大片水塘分成n小片水塘，在總共2n小片水塘中，隨機選n小片水塘種植品種A，另外n小片水塘種植B．
(1)假設n＝4，在第一大片水塘中，種植品種A的小片水塘的數目記為ξ，求ξ的分布列和數學期望；
(2)試驗時每大片水塘分成8小片，即n＝8，試驗結束后得到品種A和品種B在每個小片水塘上的每畝產量(單位：kg/畝)如下表：
分別求品種A和品種B的每畝產量的樣本平均數和樣本方差；根據試驗結果，你認為應該種植哪一品種？
| b |
| 128 |
| b |
| 128 |
設函數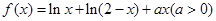
．
(Ⅰ) 當
時，求
的單調區間；
(Ⅱ) 若在
上的最大值為
，求
的值．
【解析】第一問中利用函數
的定義域為（0，2），
.
當a=1時，
所以的單調遞增區間為（0，
），單調遞減區間為（，2）；
第二問中，利用當
時，
>0, 即在上單調遞增，故在上的最大值為f(1)=a 因此a=1/2.
解：函數的定義域為（0，2），.
（1）當
時，所以的單調遞增區間為（0，），單調遞減區間為（，2）；
（2）當
時，
>0, 即在上單調遞增，故在上的最大值為f(1)=a 因此a=1/2.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com