
題目列表(包括答案和解析)
如圖1,在直角梯形 中,
中,  ,
,
把△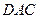 沿對(duì)角線
沿對(duì)角線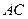 折起后如圖2所示(點(diǎn)
折起后如圖2所示(點(diǎn) 記為點(diǎn)
記為點(diǎn) ), 點(diǎn)
), 點(diǎn) 在平面
在平面 上的正投影
上的正投影 落在線段
落在線段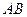 上, 連接
上, 連接 .
.
(1) 求直線 與平面
與平面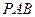 所成的角的大小;
所成的角的大小;
(2) 求二面角 的大小的余弦值.
的大小的余弦值.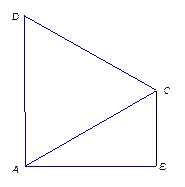

圖1 圖2
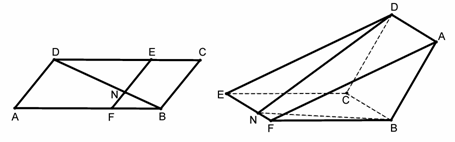
如圖,已知![]() 為平行四邊形,
為平行四邊形,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,現(xiàn)將四邊形
,現(xiàn)將四邊形![]() 沿
沿![]() 折起,使點(diǎn)
折起,使點(diǎn)![]() 在平面
在平面![]() 上的射影恰在直線
上的射影恰在直線![]() 上.
上.
(Ⅰ) 求證:![]() 平面
平面![]() ;
;
(Ⅱ) 求折后直線![]() 與直線
與直線![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ) 求三棱錐![]() 的體積.
的體積.
如圖1,在直角梯形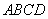 中,
中, 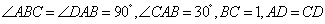 ,
,
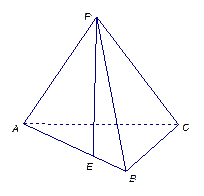
把△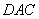 沿對(duì)角線
沿對(duì)角線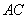 折起后如圖2所示(點(diǎn)
折起后如圖2所示(點(diǎn)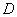 記為點(diǎn)
記為點(diǎn) ),
點(diǎn)
),
點(diǎn) 在平面
在平面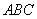 上的正投影
上的正投影 落在線段
落在線段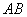 上, 連接
上, 連接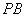 .
.
(1) 求直線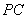 與平面
與平面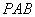 所成的角的大小;
所成的角的大小;
(2) 求二面角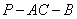 的大小的余弦值.
的大小的余弦值.
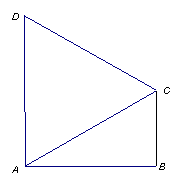

圖1 圖2
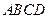 中,
中, 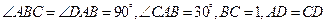 ,
,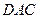 沿對(duì)角線
沿對(duì)角線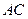 折起后如圖2所示(點(diǎn)
折起后如圖2所示(點(diǎn)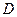 記為點(diǎn)
記為點(diǎn)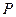 ), 點(diǎn)
), 點(diǎn)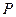 在平面
在平面 上的正投影
上的正投影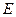 落在線段
落在線段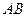 上, 連接
上, 連接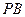 .
. 與平面
與平面 所成的角的大小;
所成的角的大小; 的大小的余弦值.
的大小的余弦值.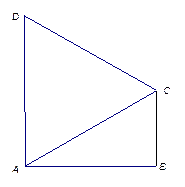
如圖,已知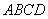 為平行四邊形,
為平行四邊形,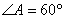 ,
,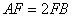 ,
,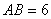 ,點(diǎn)
,點(diǎn)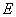 在
在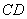 上,
上,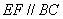 ,
, ,
,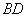 與
與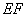 相交于
相交于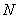 .現(xiàn)將四邊形
.現(xiàn)將四邊形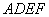 沿
沿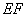 折起,使點(diǎn)
折起,使點(diǎn)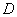 在平面
在平面 上的射影恰在直線
上的射影恰在直線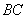 上.
上.

(Ⅰ) 求證: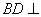 平面
平面 ;
;
(Ⅱ) 求折后直線 與平面
與平面 所成角的余弦值.
所成角的余弦值.
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
1. A 2. B 3. C 4. A 5.B
6. D 7. A 8. C 9. D 10.C
二、填空題:本大題共4小題,每小題4分,共16分.
11. 學(xué).files/image287.gif) 12.
12.學(xué).files/image289.gif) 13.24
14.
13.24
14.學(xué).files/image291.gif)
15.168 16.①②③ 17.1:(-6):5:(-8)
三、解答題:本大題共6小題,共74分.
18.解:(Ⅰ)由學(xué).files/image293.gif)
學(xué).files/image295.gif)
學(xué).files/image297.gif) ---------4分
---------4分
由學(xué).files/image178.gif) ,得
,得學(xué).files/image299.gif)
即學(xué).files/image301.gif)
則學(xué).files/image303.gif) ,即
,即學(xué).files/image018.gif) 為鈍角,故
為鈍角,故學(xué).files/image188.gif) 為銳角,且
為銳角,且學(xué).files/image307.gif)
則學(xué).files/image309.gif)
故學(xué).files/image311.gif) . ---------8分
. ---------8分
(Ⅱ)設(shè)學(xué).files/image313.gif) ,
,
由余弦定理得學(xué).files/image315.gif)
解得學(xué).files/image317.gif)
故學(xué).files/image319.gif) .
---------14分
.
---------14分
19.解:(1)學(xué).files/image321.gif) --------4分
--------4分
(2)x可能取的所有值有2,3,4 --------5分
學(xué).files/image323.gif)
學(xué).files/image325.gif)
學(xué).files/image327.gif) --------8分
--------8分
∴x的分布列為:
學(xué).files/image190.gif)
學(xué).files/image330.gif)
學(xué).files/image332.gif)
學(xué).files/image240.gif)
學(xué).files/image335.gif)
學(xué).files/image337.gif)
學(xué).files/image339.gif)
學(xué).files/image341.gif)
∴Ex=學(xué).files/image343.gif) --------10分
--------10分
(3)當(dāng)學(xué).files/image345.gif) 時(shí),取出的3張卡片上的數(shù)字為1,2,2或1,2,3
時(shí),取出的3張卡片上的數(shù)字為1,2,2或1,2,3
當(dāng)取出的卡片上的數(shù)字為1,2,2或1,2,3的概率為學(xué).files/image347.gif) ,
,
∴學(xué).files/image349.gif) --------14分
--------14分
學(xué).files/image351.jpg) 20.解:(Ⅰ)EF⊥DN,EF⊥BN,
20.解:(Ⅰ)EF⊥DN,EF⊥BN,
∴EF⊥平面BDN,
∴平面BDN⊥平面BCEF,
又因?yàn)锽N為平面BDN與平面BCEF的交線,
∴D在平面BCEF上的射影在直線BN上
而D在平面BCEF上的射影在BC上,
∴D在平面BCEF上的射影即為點(diǎn)B,即BD⊥平面BCEF. --------4分
(Ⅱ)法一.如圖,建立空間直角坐標(biāo)系,
∵在原圖中AB=6,∠DAB=60°,
則BN=學(xué).files/image353.gif) ,DN=
,DN=學(xué).files/image355.gif) ,∴折后圖中BD=3,BC=3
,∴折后圖中BD=3,BC=3
∴學(xué).files/image357.gif) ,
,
學(xué).files/image359.gif)
∴學(xué).files/image361.gif)
學(xué).files/image363.gif)
∴學(xué).files/image365.gif)
∴折后直線DN與直線BF所成角的余弦值為學(xué).files/image367.gif) . --------9分
. --------9分
法二.在線段BC上取點(diǎn)M,使BM=FN,則MN//BF
∴∠DNM或其補(bǔ)角為DN與BF所成角。
又MN=BF=2, DM=學(xué).files/image369.gif) ,
,學(xué).files/image371.gif) 。
。
∴學(xué).files/image373.gif)
∴折后直線DN與直線BF所成角的余弦值為學(xué).files/image367.gif) 。
。
(Ⅲ)∵AD//EF,
∴A到平面BNF的距離等于D到平面BNF的距離,
∴學(xué).files/image375.gif)
即所求三棱錐的體積為學(xué).files/image377.gif) . --------14分
. --------14分
21.解:(Ⅰ)(?)由已知可得學(xué).files/image379.gif) ,
,
則所求橢圓方程學(xué).files/image381.gif) . --------3分
. --------3分
(?)由已知可得動(dòng)圓圓心軌跡為拋物線,且拋物線學(xué).files/image018.gif) 的焦點(diǎn)為
的焦點(diǎn)為學(xué).files/image383.gif) ,準(zhǔn)線方程為
,準(zhǔn)線方程為學(xué).files/image248.gif) ,則動(dòng)圓圓心軌跡方程為
,則動(dòng)圓圓心軌跡方程為學(xué).files/image386.gif) . --------6分
. --------6分
(Ⅱ)當(dāng)直線MN的斜率不存在時(shí),|MN|=4,
此時(shí)PQ的長即為橢圓長軸長,|PQ|=4,
從而學(xué).files/image388.gif) .
--------8分
.
--------8分
設(shè)直線學(xué).files/image390.gif) 的斜率為
的斜率為學(xué).files/image392.gif) ,則
,則學(xué).files/image394.gif) ,直線
,直線學(xué).files/image390.gif) 的方程為:
的方程為:學(xué).files/image397.gif)
直線PQ的方程為學(xué).files/image399.gif) ,
,
設(shè)學(xué).files/image401.gif)
由學(xué).files/image403.gif) ,消去
,消去學(xué).files/image405.gif) 可得
可得學(xué).files/image407.gif)
由拋物線定義可知:
學(xué).files/image409.gif) ----10分
----10分
由學(xué).files/image411.gif) ,消去
,消去學(xué).files/image405.gif) 得
得學(xué).files/image414.gif) ,
,
從而學(xué).files/image416.gif) ,
--------12分
,
--------12分
∴學(xué).files/image418.gif)
令學(xué).files/image420.gif) ,
,
∵k>0,則學(xué).files/image422.gif)
則學(xué).files/image424.gif)
學(xué).files/image426.gif)
所以學(xué).files/image428.gif) --------14分
--------14分
所以四邊形學(xué).files/image268.gif) 面積的最小值為8.
--------15分
面積的最小值為8.
--------15分
22.解:(Ⅰ)學(xué).files/image430.gif)
學(xué).files/image432.gif)
∵學(xué).files/image272.gif) 為
為學(xué).files/image435.gif) 的極值點(diǎn),∴
的極值點(diǎn),∴學(xué).files/image437.gif)
∴學(xué).files/image439.gif) 且
且學(xué).files/image441.gif)
∴學(xué).files/image443.gif) .
.
又當(dāng)學(xué).files/image443.gif) 時(shí),
時(shí),學(xué).files/image446.gif) ,從而
,從而學(xué).files/image448.gif) 為
為學(xué).files/image435.gif) 的極值點(diǎn)成立。
的極值點(diǎn)成立。
--------4分
(Ⅱ)因?yàn)?sub>學(xué).files/image435.gif) 在
在學(xué).files/image278.gif) 上為增函數(shù),
上為增函數(shù),
所以學(xué).files/image452.gif) 在
在學(xué).files/image278.gif) 上恒成立. --------6分
上恒成立. --------6分
若學(xué).files/image443.gif) ,則
,則學(xué).files/image456.gif) ,
,
∴學(xué).files/image435.gif) 在
在學(xué).files/image278.gif) 上為增函數(shù)不成立;
上為增函數(shù)不成立;
若學(xué).files/image459.gif) ,由
,由學(xué).files/image461.gif) 對(duì)
對(duì)學(xué).files/image463.gif) 恒成立知
恒成立知學(xué).files/image465.gif) 。
。
所以學(xué).files/image467.gif) 對(duì)
對(duì)學(xué).files/image469.gif) 上恒成立。
上恒成立。
令學(xué).files/image471.gif) ,其對(duì)稱軸為
,其對(duì)稱軸為學(xué).files/image473.gif) ,
,
因?yàn)?sub>學(xué).files/image465.gif) ,所以
,所以學(xué).files/image475.gif) ,從而
,從而學(xué).files/image477.gif) 在
在學(xué).files/image278.gif) 上為增函數(shù)。
上為增函數(shù)。
所以只要學(xué).files/image479.gif) 即可,即
即可,即學(xué).files/image481.gif)
所以學(xué).files/image483.gif)
又因?yàn)?sub>學(xué).files/image465.gif) ,所以
,所以學(xué).files/image486.gif) .
--------10分
.
--------10分
(Ⅲ)若學(xué).files/image281.gif) 時(shí),方程
時(shí),方程學(xué).files/image283.gif)
可得學(xué).files/image489.gif)
即學(xué).files/image491.gif) 在
在學(xué).files/image493.gif) 上有解
上有解
即求函數(shù)學(xué).files/image495.gif) 的值域.
的值域.
法一:學(xué).files/image497.gif)
令學(xué).files/image499.gif)
由學(xué).files/image501.gif)
∵學(xué).files/image493.gif)
∴當(dāng)學(xué).files/image503.gif) 時(shí),
時(shí),學(xué).files/image505.gif) ,從而
,從而學(xué).files/image507.gif) 在(0,1)上為增函數(shù);
在(0,1)上為增函數(shù);
當(dāng)學(xué).files/image463.gif) 時(shí),
時(shí),學(xué).files/image510.gif) ,從而
,從而學(xué).files/image507.gif) 在(1,+∞)上為減函數(shù)。
在(1,+∞)上為減函數(shù)。
∴學(xué).files/image513.gif) ,而
,而學(xué).files/image507.gif) 可以無窮小。
可以無窮小。
∴學(xué).files/image516.gif) 的取值范圍為
的取值范圍為學(xué).files/image518.gif) .
--------15分
.
--------15分
法二:學(xué).files/image520.gif)
學(xué).files/image522.gif)
當(dāng)學(xué).files/image524.gif) 時(shí),
時(shí),學(xué).files/image526.gif) ,所以
,所以學(xué).files/image528.gif) 在
在學(xué).files/image524.gif) 上遞增;
上遞增;
當(dāng)學(xué).files/image530.gif) 時(shí),
時(shí),學(xué).files/image532.gif) ,所以
,所以學(xué).files/image528.gif) 在
在學(xué).files/image530.gif) 上遞減;
上遞減;
又學(xué).files/image536.gif) ,∴令
,∴令學(xué).files/image538.gif) ,
,學(xué).files/image540.gif) .
.
∴當(dāng)學(xué).files/image542.gif) 時(shí),
時(shí),學(xué).files/image544.gif) ,所以
,所以學(xué).files/image546.gif) 在
在學(xué).files/image542.gif) 上遞減;
上遞減;
當(dāng)學(xué).files/image549.gif) 時(shí),
時(shí),學(xué).files/image551.gif) ,所以
,所以學(xué).files/image546.gif) 在
在學(xué).files/image549.gif) 上遞增;
上遞增;
當(dāng)學(xué).files/image463.gif) 時(shí),
時(shí),學(xué).files/image544.gif) ,所以
,所以學(xué).files/image546.gif) 在
在學(xué).files/image463.gif) 上遞減;
上遞減;
又當(dāng)學(xué).files/image558.gif) 時(shí),
時(shí),學(xué).files/image560.gif) ,
,
學(xué).files/image562.gif)
當(dāng)學(xué).files/image564.gif) 時(shí),
時(shí), 學(xué).files/image566.gif) ,則
,則學(xué).files/image568.gif) ,且
,且學(xué).files/image570.gif)
所以學(xué).files/image516.gif) 的取值范圍為
的取值范圍為學(xué).files/image518.gif) . --------15
. --------15
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com