
題目列表(包括答案和解析)
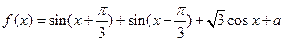 的最大值為3
的最大值為3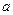 的值;
的值;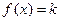 在
在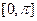 有兩個(gè)不相等的實(shí)數(shù)根,求實(shí)數(shù)
有兩個(gè)不相等的實(shí)數(shù)根,求實(shí)數(shù)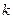 的取值范圍
的取值范圍若![]() 的最大值為m,且f(x)為偶函數(shù),求實(shí)數(shù)m+u=________.
的最大值為m,且f(x)為偶函數(shù),求實(shí)數(shù)m+u=________.
設(shè)![]() .
.
(Ⅰ)求![]() 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若銳角![]() 滿足
滿足![]() ,求
,求![]() 的值.
的值.
![]() .
.
(1)若![]() 求
求![]() 的單調(diào)區(qū)間及
的單調(diào)區(qū)間及![]() 的最小值;
的最小值;
(2)若![]() ,求
,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)試比較![]() 與
與![]() 的大小.
的大小.![]() ,并證明你的結(jié)論.
,并證明你的結(jié)論.
已知![]()
![]() .
.
(1)求![]() 的最大值;
的最大值;
(2)記DABC的內(nèi)角A、B、C的對(duì)邊分別為![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() ,求
,求![]() .
.
一、選擇題:(共8題,每小題5分,滿分40分)
題號(hào)
1
2
3
4
5
6
7
8
答案
A
C
D
C
A
D
B
B
二、填空題:(每題5分,共30分)
9.
8 10.
60 11. 8
12. 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image235.gif)
13.
10或0(答對(duì)一個(gè)給3分) 14. 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image237.gif) 15.
15. 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image239.gif)
三、解答題(本大題共6小題,共80分)
16.(本題滿分12分)
解:(Ⅰ) 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image166.gif) =
=年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image241.gif) ……1分
……1分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image168.gif) =
=年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image243.gif) ……2分
……2分
∵年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image170.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image245.gif) ……4分
……4分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image247.gif) ……6分
……6分
∵年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image249.gif) ……7分
……7分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image251.gif) .……8分
.……8分
(Ⅱ)在年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image162.gif) 中,
中,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image253.gif) ,
,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image255.gif) ,
,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image257.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image259.gif) ……9分
……9分
由正弦定理知:年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image261.gif) ……10分
……10分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image265.gif) =
=年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image267.gif) .
.
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image270.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image272.gif) ……12分
……12分
17. 本題滿分12分
解:(Ⅰ)由 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image274.gif) 知
知年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image276.gif) 是方程
是方程年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image278.gif) 的兩根,注意到
的兩根,注意到年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image280.gif) 得
得 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image282.gif) .……2分
.……2分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image285.gif) 得
得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image287.gif) .
.
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image290.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) 等比數(shù)列.
等比數(shù)列.年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image175.gif) 的公比為
的公比為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image293.gif) ,
,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image295.gif) ……4分
……4分
(Ⅱ)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image297.gif) ……5分
……5分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image299.gif) ……7分
……7分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) 數(shù)列
數(shù)列年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image184.gif) 是首項(xiàng)為3,公差為1的等差數(shù)列. ……8分
是首項(xiàng)為3,公差為1的等差數(shù)列. ……8分
(Ⅲ) 由(Ⅱ)知數(shù)列年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image184.gif) 是首項(xiàng)為3,公差為1的等差數(shù)列,有
是首項(xiàng)為3,公差為1的等差數(shù)列,有
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image186.gif) ……
……年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image303.gif) =
=年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image305.gif) ……
……年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image307.gif)
=年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image309.gif) ……10分
……10分
∵年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image311.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image314.gif) ,整理得
,整理得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image316.gif) ,解得
,解得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image318.gif) .
.年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image320.gif) ……11分
……11分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image322.gif) 的最大值是7. ……12分
的最大值是7. ……12分
18. 本題滿分14分
解: (Ⅰ)從2種服裝商品,2種家電商品,3種日用商品中,選出3種商品一共有年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image324.gif) 種選法,.選出的3種商品中沒(méi)有日用商品的選法有
種選法,.選出的3種商品中沒(méi)有日用商品的選法有年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image326.gif) 種, 所以選出的3種商品中至少有一種日用商品的概率為
種, 所以選出的3種商品中至少有一種日用商品的概率為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image328.gif) .……4分
.……4分
(Ⅱ)顧客在三次抽獎(jiǎng)中所獲得的獎(jiǎng)金總額是一隨機(jī)變量,設(shè)為X,其所有可能值為0, 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image190.gif) ,2
,2年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image190.gif) ,3
,3年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image190.gif) .……6分
.……6分
X=0時(shí)表示顧客在三次抽獎(jiǎng)中都沒(méi)有獲獎(jiǎng),所以年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image333.gif) ……7分
……7分
同理可得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image335.gif) ……8分
……8分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image337.gif) ……9分
……9分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image339.gif) ……10分
……10分
于是顧客在三次抽獎(jiǎng)中所獲得的獎(jiǎng)金總額的期望值是年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image341.gif) .……12分
.……12分
要使促銷方案對(duì)商場(chǎng)有利,應(yīng)使顧客獲獎(jiǎng)獎(jiǎng)金總額的期望值不大于商場(chǎng)的提價(jià)數(shù)額,因此應(yīng)有年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image343.gif) ,所以
,所以年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image345.gif) , …… 13分
, …… 13分
故商場(chǎng)應(yīng)將中獎(jiǎng)獎(jiǎng)金數(shù)額最高定為100元,才能使促銷方案對(duì)商場(chǎng)有利. …… 14分
19.本題滿分14分
.解:(Ⅰ) 證明:方法一)連AC,BD交于O點(diǎn),連GO,FO,EO.
∵E,F分別為PC,PD的中點(diǎn),∴年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image347.gif) //
//年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image349.gif) ,同理
,同理年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image351.gif) //
//年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image353.gif) ,
, 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image355.gif) //
// 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image351.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) 四邊形EFOG是平行四邊形,
四邊形EFOG是平行四邊形, 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image358.gif) 平面EFOG. ……3分
平面EFOG. ……3分
又在三角形PAC中,E,O分別為PC,AC的中點(diǎn),年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) PA//EO……4分
PA//EO……4分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image361.gif) 平面EFOG,PA
平面EFOG,PA年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image363.gif) 平面EFOG, ……5分
平面EFOG, ……5分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) PA//平面EFOG,即PA//平面EFG. ……6分
PA//平面EFOG,即PA//平面EFG. ……6分
方法二) 連AC,BD交于O點(diǎn),連GO,FO,EO.
∵E,F分別為PC,PD的中點(diǎn),∴年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image347.gif) //
//年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image349.gif) ,同理
,同理年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image366.gif) //
//年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image368.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image370.gif) 又
又年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image372.gif) //AB,
//AB,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image355.gif) //
//年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image375.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image377.gif) 平面EFG//平面PAB, ……4分
平面EFG//平面PAB, ……4分
又PA年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image363.gif) 平面PAB,
平面PAB,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image380.gif) 平面EFG. ……6分
平面EFG. ……6分
方法三)如圖以D為原點(diǎn),以年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image382.gif)
為方向向量建立空間直角坐標(biāo)系年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image384.gif) .
.
則有關(guān)點(diǎn)及向量的坐標(biāo)為:
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image386.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image388.gif) ……2分
……2分
設(shè)平面EFG的法向量為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image390.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image392.gif)
取年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image394.gif) .……4分
.……4分
∵年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image396.gif) ,……5分
,……5分
又年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image398.gif) 平面EFG.
平面EFG.
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) AP//平面EFG. ……6分
AP//平面EFG. ……6分
(Ⅱ)由已知底面ABCD是正方形
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image402.gif) ,又∵
,又∵年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image201.gif) 面ABCD
面ABCD
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image405.gif)
又年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image407.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image409.gif) 平面PCD,
平面PCD,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) 向量
向量年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image412.gif) 是平面PCD的一個(gè)法向量,
是平面PCD的一個(gè)法向量, 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image412.gif) =
=年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image415.gif) ……8分
……8分
又由(Ⅰ)方法三)知平面EFG的法向量為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image394.gif) ……9分
……9分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image417.gif) ……10分
……10分
結(jié)合圖知二面角年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image205.gif) 的平面角為
的平面角為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image419.gif) ……11分
……11分
(Ⅲ)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image421.gif) ……14分
……14分
20. 本題滿分14分
(Ⅰ)由題意可得點(diǎn)A,B,C的坐標(biāo)分別為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image423.gif) .……1分
.……1分
設(shè)橢圓的標(biāo)準(zhǔn)方程是年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image425.gif) .……2分
.……2分
則年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image427.gif) ……4分
……4分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image429.gif) .……5分
.……5分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) 橢圓的標(biāo)準(zhǔn)方程是
橢圓的標(biāo)準(zhǔn)方程是年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image432.gif) ……6分
……6分
(Ⅱ)由題意直線的斜率存在,可設(shè)直線年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image220.gif) 的方程為
的方程為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image434.gif) .……7分
.……7分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image435.gif) 設(shè)M,N兩點(diǎn)的坐標(biāo)分別為
設(shè)M,N兩點(diǎn)的坐標(biāo)分別為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image437.gif)
聯(lián)立方程:年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image439.gif)
消去年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image441.gif) 整理得,
整理得,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image443.gif)
有年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image445.gif) ……9分
……9分
若以MN為直徑的圓恰好過(guò)原點(diǎn),則年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image447.gif) ,所以
,所以年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image449.gif) ,……10分
,……10分
所以,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image451.gif) ,
,
即年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image453.gif)
所以,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image455.gif)
即年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image457.gif) ……11分 得
……11分 得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image459.gif) ……12分
……12分
所以直線年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image220.gif) 的方程為
的方程為年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image461.gif) ,或
,或年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image463.gif) .……13分
.……13分
所以存在過(guò)P(0,2)的直線年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image220.gif) :
:年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image465.gif) 使得以弦MN為直徑的圓恰好過(guò)原點(diǎn). ……14分
使得以弦MN為直徑的圓恰好過(guò)原點(diǎn). ……14分
21: 本題滿分14分
(Ⅰ)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image467.gif)
……2分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image469.gif) ……4分
……4分
(Ⅱ)
(?)0<t<t+2<年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image471.gif) ,t無(wú)解;……5分
,t無(wú)解;……5分
(?)0<t<年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image471.gif) <t+2,即0<t<
<t+2,即0<t<年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image471.gif) 時(shí),
時(shí),年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image473.gif) ;……7分
;……7分
(?)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image471.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image475.gif) ,即
,即年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image477.gif) 時(shí),
時(shí),年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image479.gif) ,
,年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image481.gif) ……9分
……9分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image483.gif) ……10分
……10分
(Ⅲ)由題意:年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image485.gif)
即年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image487.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image489.gif)
可得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image491.gif) ……11分
……11分
設(shè)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image493.gif) ,
,
則年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image495.gif) ……12分
……12分
令年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image497.gif) ,得
,得年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image499.gif) (舍)
(舍)
當(dāng)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image501.gif) 時(shí),
時(shí),年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image503.gif) ;當(dāng)
;當(dāng)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image505.gif) 時(shí),
時(shí), 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image507.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image263.gif) 當(dāng)
當(dāng)年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image510.gif) 時(shí),
時(shí),年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image512.gif) 取得最大值,
取得最大值, 年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image512.gif)
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image515.gif) =-2……13分
=-2……13分
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image517.gif) .
.
年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image519.gif) 的取值范圍是
的取值范圍是年第一學(xué)期高三質(zhì)量監(jiān)測(cè)-理科數(shù)學(xué).files/image521.gif) .……14分
.……14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com