
題目列表(包括答案和解析)
(本小題14分)已知點(1, )是函數
)是函數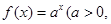 且
且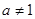 )的圖象上一點,
)的圖象上一點,
等比數列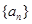 的前
的前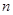 項和為
項和為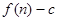 ,數列
,數列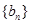
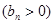 的首項為
的首項為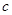 ,且前
,且前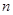 項和
項和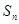 滿足
滿足
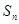 -
-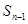 =
=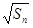 +
+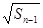 (
(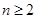 ).
).
(1)求數列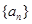 和
和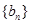 的通項公式;
的通項公式;
(2)若數列{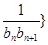 前
前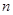 項和為
項和為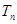 ,問
,問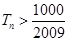 的最小正整數
的最小正整數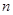 是多少?
是多少?
(3)設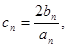 求數列
求數列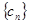 的前
的前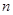 項和
項和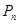
(本小題滿分14分) 已知函數![]() 及正整數數列
及正整數數列![]() . 若
. 若![]() ,且當
,且當![]() 時,有
時,有![]() ; 又
; 又![]() ,
,![]() ,且
,且![]() 對任意
對任意![]() 恒成立. 數列
恒成立. 數列![]() 滿足:
滿足:![]() .
.
(1) 求數列![]() 及
及![]() 的通項公式;
的通項公式;
(2) 求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3) 證明存在![]() ,使得
,使得![]() 對任意
對任意![]() 均成立.
均成立.
本小題滿分14分)已知正項數列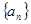 的前
的前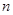 項和為
項和為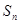 ,且滿足
,且滿足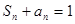 .
.
(I) 求數列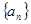 的通項公式;
的通項公式;
(Ⅱ)設數列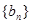 滿足
滿足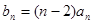 ,且數列
,且數列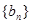 的前
的前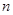 項和為
項和為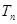 ,
,
求證:數列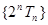 為等差數列.
為等差數列.
(本小題滿分14分)
已知函數 .
.
(1)討論 函數
函數 的單調性;
的單調性;
(2)當 為偶數時,正項數列
為偶數時,正項數列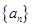 滿足
滿足 ,求
,求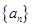 的通項公式;
的通項公式;
(3)當 為奇數且
為奇數且 時,求證:
時,求證: .
.
(本小題滿分14分)
已知等比數列![]() 的前
的前![]() 項和
項和![]() =
=![]() 數列
數列![]()
![]() 的首項為
的首項為![]() ,且前
,且前![]() 項和
項和![]() 滿足
滿足![]() -
-![]() =1(
=1(![]() ).
).
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的通項公式;
的通項公式;
(3)若數列{![]() 前
前![]() 項和為
項和為![]() ,問
,問![]() >
>![]() 的最小正整數
的最小正整數![]() 是多少? .
是多少? .
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.A 2.B 3.C 4.A 5.B
6.D 7.A 8.C 9.D 10.C
二、填空題:本大題共4小題,每小題4分,共16分.
11.卷.files/image309.gif) 12.
12.卷.files/image311.gif) 13.
13.卷.files/image313.gif) 或
或卷.files/image315.gif) 14.
14.卷.files/image317.gif)
15.卷.files/image200.gif) 16.
16.卷.files/image320.gif) (也可表示成
(也可表示成卷.files/image322.gif) ) 17.①②③
) 17.①②③
三、解答題:本大題共6小題,共74分.
18.解:(Ⅰ)由卷.files/image324.gif)
卷.files/image326.gif)
卷.files/image328.gif) ---------4分
---------4分
由卷.files/image194.gif) ,得
,得卷.files/image330.gif)
即卷.files/image332.gif)
則卷.files/image334.gif) ,即
,即卷.files/image021.gif) 為鈍角,故
為鈍角,故卷.files/image204.gif) 為銳角,且
為銳角,且卷.files/image338.gif)
則卷.files/image340.gif)
故卷.files/image342.gif) .
---------8分
.
---------8分
(Ⅱ)設卷.files/image344.gif) ,
,
由余弦定理得卷.files/image346.gif)
解得卷.files/image348.gif)
故卷.files/image350.gif) .
---------14分
.
---------14分
19.解:(Ⅰ)由卷.files/image352.gif) ,得
,得卷.files/image354.gif) 面
面卷.files/image356.gif)
則平面卷.files/image358.gif) 平面
平面卷.files/image233.gif) ,
,
由卷.files/image360.gif) 平面
平面卷.files/image362.gif) 平面
平面卷.files/image233.gif) ,
,
則卷.files/image231.gif) 在平面
在平面卷.files/image233.gif) 上的射影在直線
上的射影在直線卷.files/image364.gif) 上,
上,
又卷.files/image231.gif) 在平面
在平面卷.files/image233.gif) 上的射影在直線
上的射影在直線卷.files/image196.gif) 上,
上,
則卷.files/image231.gif) 在平面
在平面卷.files/image233.gif) 上的射影即為點
上的射影即為點卷.files/image204.gif) ,
,
故卷.files/image236.gif) 平面
平面卷.files/image233.gif) .
--------6分
.
--------6分
(Ⅱ)連接卷.files/image367.gif) ,由
,由卷.files/image236.gif) 平面
平面卷.files/image233.gif) ,得
,得卷.files/image369.gif) 即為直線
即為直線卷.files/image239.gif) 與平面
與平面卷.files/image233.gif) 所成角。
所成角。
在原圖中,由已知,可得卷.files/image371.gif)
折后,由卷.files/image236.gif) 平面
平面卷.files/image233.gif) ,知
,知卷.files/image373.gif)
則卷.files/image375.gif) ,即
,即卷.files/image377.gif)
則在卷.files/image379.gif) 中,有
中,有卷.files/image377.gif) ,
,卷.files/image382.gif) ,則
,則卷.files/image384.gif) ,
,
故卷.files/image386.gif)
即折后直線卷.files/image239.gif) 與平面
與平面卷.files/image233.gif) 所成角的余弦值為
所成角的余弦值為卷.files/image388.gif) .
--------14分
.
--------14分
20.解:(Ⅰ)由卷.files/image247.gif) ,
,卷.files/image249.gif)
得卷.files/image390.gif)
卷.files/image392.gif)
又卷.files/image394.gif) ,故
,故卷.files/image396.gif)
故數列卷.files/image251.gif) 為等比數列;
--------6分
為等比數列;
--------6分
(Ⅱ)由(Ⅰ)可知卷.files/image398.gif) ,
,
則卷.files/image400.gif)
則卷.files/image402.gif) 對任意的
對任意的卷.files/image404.gif) 恒成立
恒成立
由不等式卷.files/image406.gif) 對
對卷.files/image262.gif) 恒成立,得
恒成立,得卷.files/image408.gif)
卷.files/image410.gif) .
--------14分
.
--------14分
21.解:卷.files/image412.gif)
(Ⅰ)由已知可得卷.files/image414.gif)
此時卷.files/image416.gif) ,
--------4分
,
--------4分
由卷.files/image418.gif) 得
得卷.files/image269.gif) 的單調遞減區間為
的單調遞減區間為卷.files/image420.gif) ;----7分
;----7分
(Ⅱ)由已知可得卷.files/image422.gif) 在
在卷.files/image276.gif) 上存在零點且在零點兩側
上存在零點且在零點兩側卷.files/image422.gif) 值異號
值異號
⑴卷.files/image425.gif) 時,
時,卷.files/image427.gif) ,不滿足條件;
,不滿足條件;
⑵卷.files/image429.gif) 時,可得
時,可得卷.files/image431.gif) 在
在卷.files/image276.gif) 上有解且
上有解且卷.files/image433.gif)
設卷.files/image435.gif)
①當卷.files/image437.gif) 時,滿足
時,滿足卷.files/image439.gif) 在
在卷.files/image276.gif) 上有解
上有解
卷.files/image441.gif) 或
或卷.files/image443.gif) 此時滿足
此時滿足卷.files/image433.gif)
②當卷.files/image445.gif) 時,即
時,即卷.files/image439.gif) 在
在卷.files/image276.gif) 上有兩個不同的實根
上有兩個不同的實根
則卷.files/image447.gif)
卷.files/image045.gif) 無解
無解
綜上可得實數卷.files/image045.gif) 的取值范圍為
的取值范圍為卷.files/image450.gif) .
--------15分
.
--------15分
22.解:(Ⅰ)(?)由已知可得卷.files/image452.gif) ,
,
則所求橢圓方程卷.files/image454.gif) . --------3分
. --------3分
(?)由已知可得動圓圓心軌跡為拋物線,且拋物線卷.files/image021.gif) 的焦點為
的焦點為卷.files/image456.gif) ,準線方程為
,準線方程為卷.files/image289.gif) ,則動圓圓心軌跡方程為
,則動圓圓心軌跡方程為卷.files/image459.gif) .
--------6分
.
--------6分
(Ⅱ)由題設知直線卷.files/image461.gif) 的斜率均存在且不為零
的斜率均存在且不為零
設直線卷.files/image463.gif) 的斜率為
的斜率為卷.files/image465.gif) ,
,卷.files/image467.gif) ,則直線
,則直線卷.files/image463.gif) 的方程為:
的方程為:卷.files/image470.gif)
聯立卷.files/image459.gif)
消去卷.files/image472.gif) 可得
可得卷.files/image474.gif) --------8分
--------8分
由拋物線定義可知:
卷.files/image476.gif) -----10分
-----10分
同理可得卷.files/image478.gif) --------11分
--------11分
又卷.files/image480.gif)
(當且僅當卷.files/image482.gif) 時取到等號)
時取到等號)
所以四邊形卷.files/image307.gif) 面積的最小值為
面積的最小值為卷.files/image484.gif) .
--------15分
.
--------15分
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com