
題目列表(包括答案和解析)
設(shè)橢圓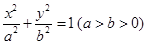 的左右頂點(diǎn)分別為
的左右頂點(diǎn)分別為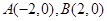 ,離心率
,離心率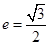 .過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且
.過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且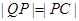 .
.
(1)求橢圓的方程;
(2)求動(dòng)點(diǎn)C的軌跡E的方程;
(3)設(shè)直線AC(C點(diǎn)不同于A,B)與直線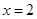 交于點(diǎn)R,D為線段RB的中點(diǎn),試判斷直線CD與曲線E的位置關(guān)系,并證明你的結(jié)論.
交于點(diǎn)R,D為線段RB的中點(diǎn),試判斷直線CD與曲線E的位置關(guān)系,并證明你的結(jié)論.
設(shè)橢圓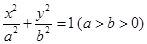 的左、右頂點(diǎn)分別為
的左、右頂點(diǎn)分別為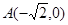 、
、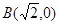 ,離心率
,離心率 .過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且
.過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且 .
.
(1)求橢圓的方程;
(2)求動(dòng)點(diǎn)C的軌跡E的方程;
(3)設(shè)直線MN過橢圓的右焦點(diǎn)與橢圓相交于M、N兩點(diǎn),且 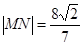 ,求直線MN的方程.
,求直線MN的方程.
設(shè)橢圓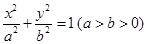 的左右頂點(diǎn)分別為
的左右頂點(diǎn)分別為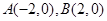 ,離心率
,離心率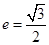 .過該橢圓上任一點(diǎn)
.過該橢圓上任一點(diǎn)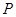 作
作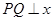 軸,垂足為
軸,垂足為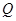 ,點(diǎn)
,點(diǎn)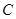 在
在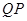 的延長線上,且
的延長線上,且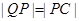 .
.
(1)求橢圓的方程;
(2)求動(dòng)點(diǎn)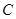 的軌跡
的軌跡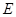 的方程;
的方程;
(3)設(shè)直線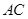 (
(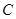 點(diǎn)不同于
點(diǎn)不同于 )與直線
)與直線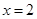 交于點(diǎn)
交于點(diǎn)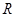 ,
,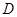 為線段
為線段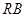 的中點(diǎn),試判斷直線
的中點(diǎn),試判斷直線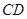 與曲線
與曲線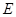 的位置關(guān)系,并證明你的結(jié)論.
的位置關(guān)系,并證明你的結(jié)論.
設(shè)橢圓 的左右頂點(diǎn)分別為
的左右頂點(diǎn)分別為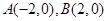 ,離心率
,離心率 .過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且
.過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且 .
.
(1)求橢圓的方程;
(2)求動(dòng)點(diǎn)C的軌跡E的方程;
(3)設(shè)直線AC(C點(diǎn)不同于A,B)與直線 交于點(diǎn)R,D為線段RB的中點(diǎn),試判斷直線CD與曲線E的位置關(guān)系,并證明你的結(jié)論.
交于點(diǎn)R,D為線段RB的中點(diǎn),試判斷直線CD與曲線E的位置關(guān)系,并證明你的結(jié)論.
設(shè)橢圓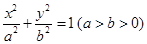 的左、右頂點(diǎn)分別為
的左、右頂點(diǎn)分別為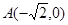 、
、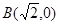 ,離心率
,離心率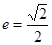 .過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且
.過該橢圓上任一點(diǎn)P作PQ⊥x軸,垂足為Q,點(diǎn)C在QP的延長線上,且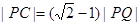 .
.
(1)求橢圓的方程;
(2)求動(dòng)點(diǎn)C的軌跡E的方程;
(3)設(shè)直線MN過橢圓的右焦點(diǎn)與橢圓相交于M、N兩點(diǎn),且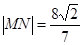 ,求直線MN的方程.
,求直線MN的方程.
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
1.A 2.B 3.C 4.A 5.B
6.D 7.A 8.C 9.D 10.C
二、填空題:本大題共4小題,每小題4分,共16分.
11.學(xué)(文科)卷.files/image309.gif) 12.
12.學(xué)(文科)卷.files/image311.gif) 13.
13.學(xué)(文科)卷.files/image313.gif) 或
或學(xué)(文科)卷.files/image315.gif) 14.
14.學(xué)(文科)卷.files/image317.gif)
15.學(xué)(文科)卷.files/image200.gif) 16.
16.學(xué)(文科)卷.files/image320.gif) (也可表示成
(也可表示成學(xué)(文科)卷.files/image322.gif) ) 17.①②③
) 17.①②③
三、解答題:本大題共6小題,共74分.
18.解:(Ⅰ)由學(xué)(文科)卷.files/image324.gif)
學(xué)(文科)卷.files/image326.gif)
學(xué)(文科)卷.files/image328.gif) ---------4分
---------4分
由學(xué)(文科)卷.files/image194.gif) ,得
,得學(xué)(文科)卷.files/image330.gif)
即學(xué)(文科)卷.files/image332.gif)
則學(xué)(文科)卷.files/image334.gif) ,即
,即學(xué)(文科)卷.files/image021.gif) 為鈍角,故
為鈍角,故學(xué)(文科)卷.files/image204.gif) 為銳角,且
為銳角,且學(xué)(文科)卷.files/image338.gif)
則學(xué)(文科)卷.files/image340.gif)
故學(xué)(文科)卷.files/image342.gif) .
---------8分
.
---------8分
(Ⅱ)設(shè)學(xué)(文科)卷.files/image344.gif) ,
,
由余弦定理得學(xué)(文科)卷.files/image346.gif)
解得學(xué)(文科)卷.files/image348.gif)
故學(xué)(文科)卷.files/image350.gif) .
---------14分
.
---------14分
19.解:(Ⅰ)由學(xué)(文科)卷.files/image352.gif) ,得
,得學(xué)(文科)卷.files/image354.gif) 面
面學(xué)(文科)卷.files/image356.gif)
則平面學(xué)(文科)卷.files/image358.gif) 平面
平面學(xué)(文科)卷.files/image233.gif) ,
,
由學(xué)(文科)卷.files/image360.gif) 平面
平面學(xué)(文科)卷.files/image362.gif) 平面
平面學(xué)(文科)卷.files/image233.gif) ,
,
則學(xué)(文科)卷.files/image231.gif) 在平面
在平面學(xué)(文科)卷.files/image233.gif) 上的射影在直線
上的射影在直線學(xué)(文科)卷.files/image364.gif) 上,
上,
又學(xué)(文科)卷.files/image231.gif) 在平面
在平面學(xué)(文科)卷.files/image233.gif) 上的射影在直線
上的射影在直線學(xué)(文科)卷.files/image196.gif) 上,
上,
則學(xué)(文科)卷.files/image231.gif) 在平面
在平面學(xué)(文科)卷.files/image233.gif) 上的射影即為點(diǎn)
上的射影即為點(diǎn)學(xué)(文科)卷.files/image204.gif) ,
,
故學(xué)(文科)卷.files/image236.gif) 平面
平面學(xué)(文科)卷.files/image233.gif) .
--------6分
.
--------6分
(Ⅱ)連接學(xué)(文科)卷.files/image367.gif) ,由
,由學(xué)(文科)卷.files/image236.gif) 平面
平面學(xué)(文科)卷.files/image233.gif) ,得
,得學(xué)(文科)卷.files/image369.gif) 即為直線
即為直線學(xué)(文科)卷.files/image239.gif) 與平面
與平面學(xué)(文科)卷.files/image233.gif) 所成角。
所成角。
在原圖中,由已知,可得學(xué)(文科)卷.files/image371.gif)
折后,由學(xué)(文科)卷.files/image236.gif) 平面
平面學(xué)(文科)卷.files/image233.gif) ,知
,知學(xué)(文科)卷.files/image373.gif)
則學(xué)(文科)卷.files/image375.gif) ,即
,即學(xué)(文科)卷.files/image377.gif)
則在學(xué)(文科)卷.files/image379.gif) 中,有
中,有學(xué)(文科)卷.files/image377.gif) ,
,學(xué)(文科)卷.files/image382.gif) ,則
,則學(xué)(文科)卷.files/image384.gif) ,
,
故學(xué)(文科)卷.files/image386.gif)
即折后直線學(xué)(文科)卷.files/image239.gif) 與平面
與平面學(xué)(文科)卷.files/image233.gif) 所成角的余弦值為
所成角的余弦值為學(xué)(文科)卷.files/image388.gif) .
--------14分
.
--------14分
20.解:(Ⅰ)由學(xué)(文科)卷.files/image247.gif) ,
,學(xué)(文科)卷.files/image249.gif)
得學(xué)(文科)卷.files/image390.gif)
學(xué)(文科)卷.files/image392.gif)
又學(xué)(文科)卷.files/image394.gif) ,故
,故學(xué)(文科)卷.files/image396.gif)
故數(shù)列學(xué)(文科)卷.files/image251.gif) 為等比數(shù)列;
--------6分
為等比數(shù)列;
--------6分
(Ⅱ)由(Ⅰ)可知學(xué)(文科)卷.files/image398.gif) ,
,
則學(xué)(文科)卷.files/image400.gif)
則學(xué)(文科)卷.files/image402.gif) 對(duì)任意的
對(duì)任意的學(xué)(文科)卷.files/image404.gif) 恒成立
恒成立
由不等式學(xué)(文科)卷.files/image406.gif) 對(duì)
對(duì)學(xué)(文科)卷.files/image262.gif) 恒成立,得
恒成立,得學(xué)(文科)卷.files/image408.gif)
學(xué)(文科)卷.files/image410.gif) .
--------14分
.
--------14分
21.解:學(xué)(文科)卷.files/image412.gif)
(Ⅰ)由已知可得學(xué)(文科)卷.files/image414.gif)
此時(shí)學(xué)(文科)卷.files/image416.gif) ,
--------4分
,
--------4分
由學(xué)(文科)卷.files/image418.gif) 得
得學(xué)(文科)卷.files/image269.gif) 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為學(xué)(文科)卷.files/image420.gif) ;----7分
;----7分
(Ⅱ)由已知可得學(xué)(文科)卷.files/image422.gif) 在
在學(xué)(文科)卷.files/image276.gif) 上存在零點(diǎn)且在零點(diǎn)兩側(cè)
上存在零點(diǎn)且在零點(diǎn)兩側(cè)學(xué)(文科)卷.files/image422.gif) 值異號(hào)
值異號(hào)
⑴學(xué)(文科)卷.files/image425.gif) 時(shí),
時(shí),學(xué)(文科)卷.files/image427.gif) ,不滿足條件;
,不滿足條件;
⑵學(xué)(文科)卷.files/image429.gif) 時(shí),可得
時(shí),可得學(xué)(文科)卷.files/image431.gif) 在
在學(xué)(文科)卷.files/image276.gif) 上有解且
上有解且學(xué)(文科)卷.files/image433.gif)
設(shè)學(xué)(文科)卷.files/image435.gif)
①當(dāng)學(xué)(文科)卷.files/image437.gif) 時(shí),滿足
時(shí),滿足學(xué)(文科)卷.files/image439.gif) 在
在學(xué)(文科)卷.files/image276.gif) 上有解
上有解
學(xué)(文科)卷.files/image441.gif) 或
或學(xué)(文科)卷.files/image443.gif) 此時(shí)滿足
此時(shí)滿足學(xué)(文科)卷.files/image433.gif)
②當(dāng)學(xué)(文科)卷.files/image445.gif) 時(shí),即
時(shí),即學(xué)(文科)卷.files/image439.gif) 在
在學(xué)(文科)卷.files/image276.gif) 上有兩個(gè)不同的實(shí)根
上有兩個(gè)不同的實(shí)根
則學(xué)(文科)卷.files/image447.gif)
學(xué)(文科)卷.files/image045.gif) 無解
無解
綜上可得實(shí)數(shù)學(xué)(文科)卷.files/image045.gif) 的取值范圍為
的取值范圍為學(xué)(文科)卷.files/image450.gif) .
--------15分
.
--------15分
22.解:(Ⅰ)(?)由已知可得學(xué)(文科)卷.files/image452.gif) ,
,
則所求橢圓方程學(xué)(文科)卷.files/image454.gif) . --------3分
. --------3分
(?)由已知可得動(dòng)圓圓心軌跡為拋物線,且拋物線學(xué)(文科)卷.files/image021.gif) 的焦點(diǎn)為
的焦點(diǎn)為學(xué)(文科)卷.files/image456.gif) ,準(zhǔn)線方程為
,準(zhǔn)線方程為學(xué)(文科)卷.files/image289.gif) ,則動(dòng)圓圓心軌跡方程為
,則動(dòng)圓圓心軌跡方程為學(xué)(文科)卷.files/image459.gif) .
--------6分
.
--------6分
(Ⅱ)由題設(shè)知直線學(xué)(文科)卷.files/image461.gif) 的斜率均存在且不為零
的斜率均存在且不為零
設(shè)直線學(xué)(文科)卷.files/image463.gif) 的斜率為
的斜率為學(xué)(文科)卷.files/image465.gif) ,
,學(xué)(文科)卷.files/image467.gif) ,則直線
,則直線學(xué)(文科)卷.files/image463.gif) 的方程為:
的方程為:學(xué)(文科)卷.files/image470.gif)
聯(lián)立學(xué)(文科)卷.files/image459.gif)
消去學(xué)(文科)卷.files/image472.gif) 可得
可得學(xué)(文科)卷.files/image474.gif) --------8分
--------8分
由拋物線定義可知:
學(xué)(文科)卷.files/image476.gif) -----10分
-----10分
同理可得學(xué)(文科)卷.files/image478.gif) --------11分
--------11分
又學(xué)(文科)卷.files/image480.gif)
(當(dāng)且僅當(dāng)學(xué)(文科)卷.files/image482.gif) 時(shí)取到等號(hào))
時(shí)取到等號(hào))
所以四邊形學(xué)(文科)卷.files/image307.gif) 面積的最小值為
面積的最小值為學(xué)(文科)卷.files/image484.gif) .
--------15分
.
--------15分
www.ks5u.com
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com