
題目列表(包括答案和解析)
| a |
| 1 | ||
|
已知函數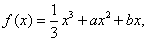 且
且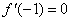
(I)試用含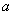 的代數式表示
的代數式表示 ;
;
(Ⅱ)求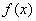 的單調區間;
的單調區間;
(Ⅲ)令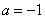 ,設函數
,設函數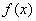 在
在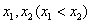 處取得極值,記點
處取得極值,記點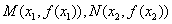 ,證明:線段
,證明:線段 與曲線
與曲線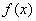 存在異于
存在異于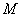 、
、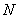 的公共點.
的公共點.
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
設直線![]() 與橢圓
與橢圓![]() 相切。 (I)試將
相切。 (I)試將![]() 用
用![]() 表示出來; (Ⅱ)若經過動點
表示出來; (Ⅱ)若經過動點![]() 可以向橢圓引兩條互相垂直的切線,
可以向橢圓引兩條互相垂直的切線,![]() 為坐標原點,求證:
為坐標原點,求證:![]() 為定值。
為定值。
(本小題滿分12分)
某中學對高二甲、乙兩個同類班級進行“加強‘語文閱讀理解,訓練對提髙‘數學應用題得分率作用”的試驗,其中甲班為試驗班(加強語文閱讀理解訓練),乙班為對比班(常規教學,無額外訓練),在試驗前的測試中,甲、乙兩班學生在數學應用題上的得分率基本一致,試驗結束后,統計幾次數學應用題測試的平均成績(均取整數)如下表所示:
| 60分以下 | 61—70 分 | 71—80 分 | 81-90 分 | 91-100分 | |
| 甲班(人數) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人數) | 8 | 13 | 15 | 10 |
現規定平均成績在80分以上(不含80分)的為優秀.
(I )試分別估計兩個班級的優秀率;
(II)由以上統計數據填寫下面2 X 2列聯表,并問是否有"5匁的把握認為“加強‘語文閱讀理解’訓練對提商‘數學應用題’得分率”有幫助.
| 優秀人數 | 非優秀人數 | 合計 | |
| 甲班 | |||
| 乙班 | |||
| 合計 |
參考公式及數據:![]() ,
,
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0. 05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
一、選擇題:每小題5分,共60分.
BABDB DCABD BD
二、填空題:本大題共4小題,每小題5分,共20分.把答案填在答題卷相應題號的橫線上.
13.某校有教師200人,男學生1200人,女學生1000人,現用分層抽樣的方法從所有老師中抽取一個容量為n的樣本;已知從女學生中抽取的人數為80人,則n的值為:16
14.若△ABC三個內角A、B、C的對邊分別是a、b、c,且acosB+bcosA=csinC,則角C的大小為:
15.若 、
、 滿足約束條件
滿足約束條件 的最大值為:2
的最大值為:2
16.若 ,且
,且 ,則實數x的取值范圍是:
,則實數x的取值范圍是:
三、解答題:本大題共6小題,共70分.把答案填在答題卷相應題號的答題區中.
17.(本小題滿分10分)
 如圖,已知
如圖,已知 ,
, ,且
,且 ,
, .
.
(I)試用 表示
表示 ;
;
(Ⅱ)設向量 和
和 的夾角為
的夾角為 ,求
,求 的值.
的值.
解:(I)設 ,則
,則
 ,
, ; …………3分
; …………3分
因 ,
, ,
, ,
,
所以
 解得:
解得:
即
 . …………5分
. …………5分
(Ⅱ)由(I)知 ,又
,又 ,
,
所以 
 )
) (
( )=
)= ,
,
 …………8分
…………8分
故  . …………10分
. …………10分
18.(本小題滿分10分)
甲、乙等五名奧運志愿者被隨機地分配到 四個不同的崗位服務,每個崗位至少有一名志愿者.
四個不同的崗位服務,每個崗位至少有一名志愿者.
(Ⅰ)求甲、乙兩人同時被分配到 崗位服務的概率;
崗位服務的概率;
(Ⅱ)求甲、乙兩人被分配到不同崗位服務的概率.
解:(Ⅰ)記甲、乙兩人同時被分到 崗位服務為事件
崗位服務為事件 ,
,
那么 ,
,
即甲、乙兩人同時被分到 崗位服務的概率是
崗位服務的概率是 . …………5分
. …………5分
(Ⅱ)設甲、乙兩人同時被分到同一崗位服務為事件 ,
,
那么 ,
,
故甲、乙兩人被分到不同崗位服務的概率是 . …………10分
. …………10分
 19.(本小題滿分12分)
19.(本小題滿分12分)
如圖,四面體ABCD中,O是BD的中點,AB=AD= ,CA=CB=CD=BD=2.
,CA=CB=CD=BD=2.
(Ⅰ)求證:AO⊥平面BCD;
(Ⅱ)求異面直線AB與CD所成角的大小.
解:(方法一)
 (Ⅰ)連結OC.∵BO=DO,AB=AD,
BC=CD,
(Ⅰ)連結OC.∵BO=DO,AB=AD,
BC=CD,
∴AO⊥BD,CO⊥BD. …………3分
在△AOC中,由已知得AC=2,AO=1,CO= ,
,
∴AO2+CO2=AC2,∴∠AOC=90°,即AO⊥OC.
 ∴AO
∴AO 平面BCD. …………6分
平面BCD. …………6分
(Ⅱ)分別取AC、BC的中點M、E,連結OM、ME、OE,則
ME∥AB,OE∥DC.
∴ (或其補角)等于異面直線AB與CD所成的角. …………9分
(或其補角)等于異面直線AB與CD所成的角. …………9分
在△OME中,
又  是直角△AOC斜邊AC上的中線,∴
是直角△AOC斜邊AC上的中線,∴
∴
∴異面直線AB與CD所成角的大小為 …………12分
…………12分
(方法二)
 (Ⅰ)同方法一. …………6分
(Ⅰ)同方法一. …………6分
(Ⅱ)由(Ⅰ)知:AO⊥OC,AO⊥BD,CO⊥BD.
以O為原點,建立空間直角坐標系如圖, …………7分
則A(0,0,1),B(1,0,0),C(0, ,0),D(-1,0,0) . …………10分
,0),D(-1,0,0) . …………10分
所以  ,
,

∴異面直線AB與CD所成角的大小為 …………12分
…………12分
20.(本小題滿分12分)
數列 滿足
滿足 ,且
,且 .
.
(I)求 ,并證明數列
,并證明數列 是等比數列;
是等比數列;
(II)求 .
.
解:(I) ,
,

 ; …………2分
; …………2分
又, , …………4分
, …………4分
且 
所以數列 是以-2為首項,3為公比的等比數列. …………6分
是以-2為首項,3為公比的等比數列. …………6分
(II)由(I)得 ,
,  . …………8分
. …………8分

 …………10分
…………10分
 …………12分
…………12分
21.(本小題滿分13分)
已知函數
 ,在任意一點
,在任意一點 處的切線的斜率為
處的切線的斜率為 .
.
(I)求函數 的單調區間;
的單調區間;
(II)若 在
在 上的最小值為
上的最小值為 ,求
,求 在R上的極大值.
在R上的極大值.
21. 解:(I)因 ,所以
,所以 ; …………2分
; …………2分
故  ,
,  ,
, ,
, ,
,
 ,
,  . …………4分
. …………4分
由 知
知 在
在 和
和 上是增函數,
上是增函數,
由 知
知 在(-1,2)上為減函數. …………8分
在(-1,2)上為減函數. …………8分
(II)由(I)知 在(-3,-1)上是增函數,在(-1,2)上為減函數,
在(-3,-1)上是增函數,在(-1,2)上為減函數,
所以  在
在 上的最小值是
上的最小值是 或
或 ,極大值為
,極大值為 . …………10分
. …………10分
而 ,
, ,
, ,
,
∴ 在
在 上的最小值是
上的最小值是 ,∴
,∴ ,
, . …………12分
. …………12分
 ,
,
即所求函數 在R上的極大值為
在R上的極大值為 …………13分
…………13分
22.(本小題滿分13分)
 如圖,傾斜角為
如圖,傾斜角為 的直線經過拋物線
的直線經過拋物線 的焦點F,且與拋物線交于A、B兩點.
的焦點F,且與拋物線交于A、B兩點.
(I)求拋物線的焦點F的坐標及準線l的方程;
(II)若 為銳角,作線段AB的垂直平分線m交x軸于點P,證明
為銳角,作線段AB的垂直平分線m交x軸于點P,證明 為定值,并求此定值.
為定值,并求此定值.
解:(I)設拋物線的標準方程為 ,則
,則 ,從而
,從而 .
.
因此拋物線焦點F的坐標為(2,0),準線方程為 . ……………4分
. ……………4分
 (II)作AC⊥l,BD⊥l,垂足分別為C、D,
(II)作AC⊥l,BD⊥l,垂足分別為C、D,
則由拋物線的定義知:|FA|=|AC|,|FB|=|BD|.
記A、B的橫坐標分別為xA、xB,則
|FA|=|AC|=
解得 ; ……………7分
; ……………7分
|FB|=|BD|=
解得 . ……………9分
. ……………9分
記直線m與AB的交點為E,則
 ,
,
所以 . ……………12分
. ……………12分
故 . ……………13分
. ……………13分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com