題目列表(包括答案和解析)
（本小題滿分12分）
如圖，在三棱錐P－ABC中，PA＝PC，∠APC＝∠ACB＝90°，∠BAC＝30°，平面PAC⊥平面ABC．
（1）求證：平面PAB⊥平面PBC；
（2）若PA＝2，求三棱錐P－ABC的體積．
（本小題滿分12分）
如圖，在三棱錐P－ABC中，AB⊥BC，AB＝BC＝PA=a，點O、D分別是AC、PC的中點，OP⊥底面ABC。
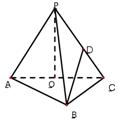
（1）求三棱錐P－ABC的體積；
（2）求異面直線PA與BD所成角余弦值的大小。
( 本小題滿分14)
如圖，在三棱錐P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分別是AB，PB的中點．
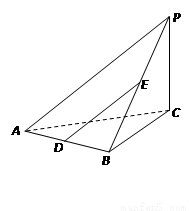
(1)求證：DE∥平面PAC
(2)求證：AB⊥PB
（本小題滿分12分）
如圖1，在三棱錐P－A.BC中，PA.⊥平面A.BC，A.C⊥BC，D為側棱PC上一點，它的正(主)視圖和側(左)視圖如圖2所示．
(1) 證明：A.D⊥平面PBC；
(2) 求三棱錐D－A.BC的體積；
(3) 在∠A.CB的平分線上確定一點Q，使得PQ∥平面A.BD，并求此時PQ的長．
（本小題15分）
如圖在三棱錐P-ABC中，PA
分別在棱
，
（1）求證：BC
（2）當D為PB中點時，求AD與平面PAC所成的角的余弦值；
(3)是否存在點E,使得二面角A-DE-P為直二面角，并說明理由。
選擇題（60分）
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D．
A
C
A
B
B
A
C
A
C
B
填空題（16分）
13 
14 
15 
16 8
17解：（1）由已知得，
………………6分
（2）
………10分
=-
………12分
18解：（Ⅰ）（法一）f(x)的定義域為R。
，
所以f(x)在
上單調遞增，在
上單調遞減。……4分
所以f(x)值域為
……6分
（法二）
……4分
所以f(x)的值域是………6分
（法三）由絕對值的幾何意義知f(x)=
表示數軸上點P（x）到點M(2)與點N(-2)距離之和．……4分
所以f(x)的值域是．……6分
（Ⅱ）原不等式等價于：
①
或②
或③
……11分
所以原不等式解集為
……12分
19 解:設
，由題意知
，
……6分
又
所以雙曲線方程為
……10分
所以雙曲線的漸近線方程為
……12分
20解：（Ⅰ）由題意知方程
的兩根是
……4分
(Ⅱ)
在[-1，2]上恒成立，………6分
令
……8分
當x在[-1,2]上變化時，
的變化情況如下：
x
-1
1
（1，2）
2
+
-
+
g(x)
ㄊ
極大值
ㄋ
極小值
ㄊ
2
所以當x=2時，
,
所以c的取值范圍為
……12分
21解：（1）當n=1時，
,當
時，由
得
所以
…………4分
所以數列
是首項為3，公差為1的等差數列，
所以數列的通項公式為
…………6分
（2）
22解 :（Ⅰ）由題設a=2,c=1從而
所以橢圓的方程為: 
………5分
（Ⅱ）由題意得F（1，0），N（4，0），設A（m,n）
則B（m,-n）(
①
設動點M（x,y）．AF與BN的方程分別為：n(x-1)-(m-1)y=0 ② n(x-4)+(m-4)y=0 ③
由②③得：當
時，
代入①得
當
時，由②③得：
，解得n=0,y=0與
矛盾,所以的軌跡方程為
。…………9分
（Ⅲ）△AMN的面積為△AFN與△MFN面積之和，且有相同的底邊FN，當兩高之和最大時，面積最大，這時AM應為特殊位置，所以猜想：當AM與x軸垂直時，△AMN的面積最大，|AM|=3，|FN|=3，這時
,△AMN的面積最大最大值為
………11分。
證明如下：設AM的方程為x=ty+1,代入
得
設A
，則有
令
，則
因為
，所以
，即
時
有最大值3，△AMN的面積有
最大值。……13分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com