
題目列表(包括答案和解析)
(本小題滿分12分)
甲乙兩名射手互不影響地進(jìn)行射擊訓(xùn)練,根據(jù)以往的數(shù)據(jù)統(tǒng)計(jì),他們?cè)O(shè)計(jì)成績(jī)的分布列如下:
|
射手甲 |
射手乙 |
||||||
|
環(huán)數(shù) |
8 |
9 |
10 |
環(huán)數(shù) |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(Ⅰ)若甲乙兩射手各射擊兩次,求四次射擊中恰有三次命中10環(huán)的概率;
(Ⅱ)若兩個(gè)射手各射擊1次,記所得的環(huán)數(shù)之和為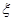 ,求
,求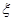 的分布列和期望.
的分布列和期望.
(本小題滿分13分)
甲乙兩名射手互不影響地進(jìn)行射擊訓(xùn)練,根據(jù)以往的數(shù)據(jù)統(tǒng)計(jì),他們?cè)O(shè)計(jì)成績(jī)的分布列如下:K^S*5U.C#O%
|
射手甲 |
射手乙 |
||||||
|
環(huán)數(shù) |
8 |
9 |
10 |
環(huán)數(shù) |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(1)若甲射手共有5發(fā)子彈,一旦命中10環(huán)就停止射擊,求他剩余3顆子彈的概率;
(2)若甲乙兩射手各射擊兩次,求四次射擊中恰有三次命中10環(huán)的概率;K^S*5U.C#O%
(3)若兩個(gè)射手各射擊1次,記所得的環(huán)數(shù)之和為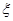 ,求
,求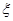 的分布列和期望。
的分布列和期望。
(本小題滿分12分)
甲乙兩名射手互不影響地進(jìn)行射擊訓(xùn)練,根據(jù)以往的數(shù)據(jù)統(tǒng)計(jì),他們?cè)O(shè)計(jì)成績(jī)的分布列如下:
| 射手甲 | 射手乙 | ||||||
| 環(huán)數(shù) | 8 | 9 | 10 | 環(huán)數(shù) | 8 | 9 | 10 |
| 概率 |  |  |  | 概率 |  |  |  |
 ,求
,求 的分布列和期望.
的分布列和期望. 設(shè)點(diǎn) 是拋物線
是拋物線

 的焦點(diǎn),
的焦點(diǎn), 是拋物線
是拋物線 上的
上的 個(gè)不同的點(diǎn)(
個(gè)不同的點(diǎn)(
 ).
).
(1) 當(dāng) 時(shí),試寫出拋物線
時(shí),試寫出拋物線 上的三個(gè)定點(diǎn)
上的三個(gè)定點(diǎn) 、
、 、
、 的坐標(biāo),從而使得
的坐標(biāo),從而使得
 ;
;
(2)當(dāng) 時(shí),若
時(shí),若 ,
,
求證: ;
;
(3) 當(dāng) 時(shí),某同學(xué)對(duì)(2)的逆命題,即:
時(shí),某同學(xué)對(duì)(2)的逆命題,即:
“若 ,則
,則 .”
.”
開展了研究并發(fā)現(xiàn)其為假命題.
請(qǐng)你就此從以下三個(gè)研究方向中任選一個(gè)開展研究:
① 試構(gòu)造一個(gè)說明該逆命題確實(shí)是假命題的反例(本研究方向最高得4分);
② 對(duì)任意給定的大于3的正整數(shù) ,試構(gòu)造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
,試構(gòu)造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
③ 如果補(bǔ)充一個(gè)條件后能使該逆命題為真,請(qǐng)寫出你認(rèn)為需要補(bǔ)充的一個(gè)條件,并說明加上該條件后,能使該逆命題為真命題的理由(本研究方向最高得10分).
【評(píng)分說明】本小題若填空不止一個(gè)研究方向,則以實(shí)得分最高的一個(gè)研究方向的得分作為本小題的最終得分.
【解析】第一問利用拋物線 的焦點(diǎn)為
的焦點(diǎn)為 ,設(shè)
,設(shè) ,
,
分別過 作拋物線
作拋物線 的準(zhǔn)線
的準(zhǔn)線 的垂線,垂足分別為
的垂線,垂足分別為 .
.
由拋物線定義得到
第二問設(shè) ,分別過
,分別過 作拋物線
作拋物線 的準(zhǔn)線
的準(zhǔn)線 垂線,垂足分別為
垂線,垂足分別為 .
.
由拋物線定義得


第三問中①取 時(shí),拋物線
時(shí),拋物線 的焦點(diǎn)為
的焦點(diǎn)為 ,
,
設(shè) ,
, 分別過
分別過
 作拋物線
作拋物線 的準(zhǔn)線
的準(zhǔn)線 垂線,垂足分別為
垂線,垂足分別為
 .由拋物線定義得
.由拋物線定義得




 ,
,
則 ,不妨取
,不妨取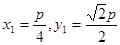 ;
;
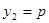 ;
;
 ;
;
解:(1)拋物線 的焦點(diǎn)為
的焦點(diǎn)為 ,設(shè)
,設(shè) ,
,
分別過 作拋物線
作拋物線 的準(zhǔn)線
的準(zhǔn)線 的垂線,垂足分別為
的垂線,垂足分別為 .由拋物線定義得
.由拋物線定義得


因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912360984321474/SYS201207091236478588145986_ST.files/image010.png">,所以 ,
,
故可取

 滿足條件.
滿足條件.
(2)設(shè) ,分別過
,分別過 作拋物線
作拋物線 的準(zhǔn)線
的準(zhǔn)線 垂線,垂足分別為
垂線,垂足分別為 .
.
由拋物線定義得


 又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912360984321474/SYS201207091236478588145986_ST.files/image017.png">
又因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070912360984321474/SYS201207091236478588145986_ST.files/image017.png">



 ;
;
所以

 .
.
(3) ①取 時(shí),拋物線
時(shí),拋物線 的焦點(diǎn)為
的焦點(diǎn)為 ,
,
設(shè) ,
, 分別過
分別過
 作拋物線
作拋物線 的準(zhǔn)線
的準(zhǔn)線 垂線,垂足分別為
垂線,垂足分別為
 .由拋物線定義得
.由拋物線定義得




 ,
,
則 ,不妨取
,不妨取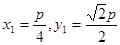 ;
;
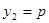 ;
;
 ;
; ,
,
則

 ,
,

 .
.
故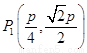 ,
, ,
, ,
, 是一個(gè)當(dāng)
是一個(gè)當(dāng) 時(shí),該逆命題的一個(gè)反例.(反例不唯一)
時(shí),該逆命題的一個(gè)反例.(反例不唯一)
② 設(shè) ,分別過
,分別過 作
作
拋物線 的準(zhǔn)線
的準(zhǔn)線 的垂線,垂足分別為
的垂線,垂足分別為 ,
,
由 及拋物線的定義得
及拋物線的定義得
 ,即
,即 .
.
因?yàn)樯鲜霰磉_(dá)式與點(diǎn) 的縱坐標(biāo)無關(guān),所以只要將這
的縱坐標(biāo)無關(guān),所以只要將這 點(diǎn)都取在
點(diǎn)都取在 軸的上方,則它們的縱坐標(biāo)都大于零,則
軸的上方,則它們的縱坐標(biāo)都大于零,則






 ,
,
而 ,所以
,所以 .
.
(說明:本質(zhì)上只需構(gòu)造滿足條件且 的一組
的一組 個(gè)不同的點(diǎn),均為反例.)
個(gè)不同的點(diǎn),均為反例.)
③ 補(bǔ)充條件1:“點(diǎn) 的縱坐標(biāo)
的縱坐標(biāo) (
( )滿足
)滿足  ”,即:
”,即:
“當(dāng) 時(shí),若
時(shí),若 ,且點(diǎn)
,且點(diǎn) 的縱坐標(biāo)
的縱坐標(biāo) (
( )滿足
)滿足 ,則
,則 ”.此命題為真.事實(shí)上,設(shè)
”.此命題為真.事實(shí)上,設(shè) ,
,
分別過 作拋物線
作拋物線 準(zhǔn)線
準(zhǔn)線 的垂線,垂足分別為
的垂線,垂足分別為 ,由
,由 ,
,
及拋物線的定義得 ,即
,即 ,則
,則






 ,
,
又由 ,所以
,所以 ,故命題為真.
,故命題為真.
補(bǔ)充條件2:“點(diǎn) 與點(diǎn)
與點(diǎn)
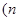 為偶數(shù),
為偶數(shù), 關(guān)于
關(guān)于 軸對(duì)稱”,即:
軸對(duì)稱”,即:
“當(dāng) 時(shí),若
時(shí),若 ,且點(diǎn)
,且點(diǎn) 與點(diǎn)
與點(diǎn)
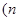 為偶數(shù),
為偶數(shù), 關(guān)于
關(guān)于 軸對(duì)稱,則
軸對(duì)稱,則 ”.此命題為真.(證略)
”.此命題為真.(證略)
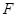 是拋物線
是拋物線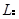
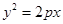
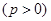 的焦點(diǎn),
的焦點(diǎn),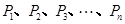 是拋物線
是拋物線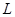 上的
上的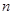 個(gè)不同的點(diǎn)(
個(gè)不同的點(diǎn)(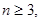
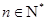 ).
).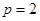 時(shí),試寫出拋物線
時(shí),試寫出拋物線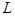 上的三個(gè)定點(diǎn)
上的三個(gè)定點(diǎn)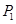 、
、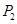 、
、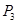 的坐標(biāo),從而使得
的坐標(biāo),從而使得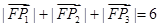 ;
;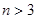 時(shí),若
時(shí),若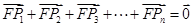 ,
, ;
;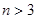 時(shí),某同學(xué)對(duì)(2)的逆命題,即:
時(shí),某同學(xué)對(duì)(2)的逆命題,即: ,則
,則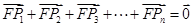 .”
.”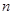 ,試構(gòu)造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
,試構(gòu)造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);一.選擇題 : 本大題共10小題, 每小題5分, 共50分.
題號(hào)
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
B
B
D
A
C
D
C
二.填空題:本大題有5小題, 每小題4分, 共20分.
11.
5 12.充分不必要 13. -1 14. 15.
15.
三.解答題:本大題有5小題, 共50分. 解答應(yīng)寫出文字說明, 證明過程或演算步驟.
16解: 因?yàn)?sub> ,所以-2<m<2;……………………………………1分
,所以-2<m<2;……………………………………1分
若方程 無實(shí)根,則
無實(shí)根,則 , ……2分
, ……2分
即 , 所以q:1<m<3. ……………………………………3分
, 所以q:1<m<3. ……………………………………3分
因?yàn)椹謕為假,則p為真,又因?yàn)閜∧q為假,則q為假. ……………………5分
所以 ……………………7分
……………………7分
所以-2<m≤1.故實(shí)數(shù) 的取值范圍為
的取值范圍為 . ………………………………8分
. ………………………………8分
17.解: (1) 由橢圓的定義知 c=6 ……1分

= ……3分
……3分

所以橢圓的標(biāo)準(zhǔn)方程為
 ……5分
……5分
(2)設(shè)雙曲線的方程為 ……8分
……8分
點(diǎn)P(5,2)代入上式得

所以雙曲線的標(biāo)準(zhǔn)方程為
 ……10分
……10分
18、解:(1)設(shè)小正方形邊長(zhǎng)為x cm,
則V=(8-2x)?(5-2x)x=4x3-26x2+40x (0<x< )
……4分
)
……4分
V′=4(3x2-13x+10) (0<x< )
)
V′=0得x=1或 (舍去)
……7分
(舍去)
……7分
 ,
,
根據(jù)實(shí)際情況,小盒容積最大是存在的,
∴當(dāng)x=
19.解:(1) 的導(dǎo)數(shù)
的導(dǎo)數(shù) .
---------2分
.
---------2分
令 ,解得
,解得 ,或
,或 ;
;
令 ,解得
,解得 .
---------4分
.
---------4分
從而 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為 ,
, ;
;
單調(diào)遞減區(qū)間為 .
---------5分
.
---------5分
(2)由(1)知
 ,
,  ---------8分
---------8分
從而當(dāng) 時(shí),函數(shù)
時(shí),函數(shù) 取得最小值
取得最小值 .
.
因?yàn)榇嬖?sub> ,使不等式
,使不等式 成立,
成立,
故 , 即
, 即  ,
---------10分
,
---------10分
20.解:(1)設(shè)拋物線方程為 ,
,
AB的方程為 ,
,
聯(lián)立消 整理,得
整理,得 ;
-------2分
;
-------2分
∴ 又依題有
又依題有 ,∴
,∴ , -------4分
, -------4分
∴拋物線方程為 ;
---------5分
;
---------5分
(2)設(shè)
 ,
,
 ,
, ,∵
,∵ ,
,
∴ 的方程為
的方程為
 ;
;
∵ 過
過 ,∴
,∴ ,同理
,同理 -------8分
-------8分
∴ 為方程
為方程 的兩個(gè)根;∴
的兩個(gè)根;∴ ;
;
又 ,∴
,∴ 的方程為
的方程為 -------11分
-------11分
∴ ,顯然直線
,顯然直線 過點(diǎn)
過點(diǎn) --------12分
--------12分
命題學(xué)校:瑞安四中(65531798) 命題人:葉海靜(13868821241)
審核學(xué)校:洞頭一中 (63480535) 審核人:陳后萬(13858823246)
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com