
題目列表(包括答案和解析)
從裝有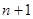 個球(其中
個球(其中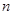 個白球,
個白球,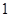 個黑球)的口袋中取出
個黑球)的口袋中取出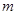 個球(
個球(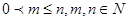 ),共有
),共有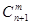
 種取法。在這
種取法。在這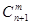 種取法中,可以分成兩類:一類是取出的
種取法中,可以分成兩類:一類是取出的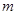 個球全部為白球,一類是取出的
個球全部為白球,一類是取出的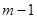 個白球和一個黑球。共有C
個白球和一個黑球。共有C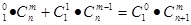 ,即等式
,即等式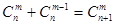 成立。根據上述思想化簡式子
成立。根據上述思想化簡式子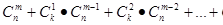
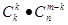 =
=
(其中1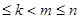 ,
,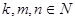 )
)
(1)已知α是第一象限的角,且cosα=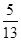 ,求
,求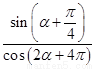 的值.
的值.
(2)化簡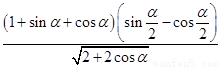 ,其中π<α<2π.
,其中π<α<2π.
已知等比數列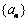 ,首項
,首項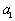 是
是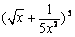 的展開式中的常數項,公比
的展開式中的常數項,公比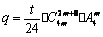 ,且
,且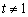 .
.
(1) 求a1及m的值;
(2) 化簡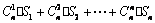 ,其中
,其中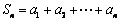 ;
;
(3) 若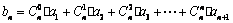 ,
,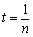 時,證明
時,證明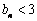 ,對任意
,對任意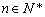 成立.
成立.
| 2+4i |
| (1+i)2 |
| A、2+i | B、-2+i |
| C、2-i | D、-2-i |
| sin[α+(2n+1)π]•2sin[α-(2n+1)π] |
| sin(α-2nπ)cos(2nπ-α) |
| sin(2π-α)sin(π+α)cos(-π-α) |
| sin(3π-α)•cos(π-α) |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com