
題目列表(包括答案和解析)
已知 是R上的奇函數且在
是R上的奇函數且在 上單調遞增,令
上單調遞增,令 ,
, 則 ( )
則 ( )
A. B.
B.
C. D.
D.
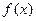 是R上的奇函數且在
是R上的奇函數且在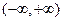 上單調遞增,令
上單調遞增,令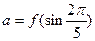 ,
,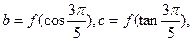 則 ( )
則 ( )A. | B. |
C. | D. |
設函數 .
.
(I)求 的單調區間;
的單調區間;
(II)當0<a<2時,求函數 在區間
在區間 上的最小值.
上的最小值.
【解析】第一問定義域為真數大于零,得到 .
. .
.
令 ,則
,則 ,所以
,所以 或
或 ,得到結論。
,得到結論。
第二問中, (
( ).
).
 .
.
因為0<a<2,所以 ,
, .令
.令 可得
可得 .
.
對參數討論的得到最值。
所以函數 在
在 上為減函數,在
上為減函數,在 上為增函數.
上為增函數.
(I)定義域為 . ………………………1分
. ………………………1分
 .
.
令 ,則
,則 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因為定義域為 ,所以
,所以 .
.
令 ,則
,則 ,所以
,所以 .
.
因為定義域為 ,所以
,所以 . ………………………5分
. ………………………5分
所以函數的單調遞增區間為 ,
,
單調遞減區間為 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因為0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函數 在
在 上為減函數,在
上為減函數,在 上為增函數.
上為增函數.
①當 ,即
,即 時,
時,
在區間 上,
上, 在
在 上為減函數,在
上為減函數,在 上為增函數.
上為增函數.
所以 . ………………………10分
. ………………………10分
②當 ,即
,即 時,
時, 在區間
在區間 上為減函數.
上為減函數.
所以 .
.
綜上所述,當 時,
時, ;
;
當 時,
時,
已知函數 .(
.( )
)
(1)若 在區間
在區間 上單調遞增,求實數
上單調遞增,求實數 的取值范圍;
的取值范圍;
(2)若在區間 上,函數
上,函數 的圖象恒在曲線
的圖象恒在曲線 下方,求
下方,求 的取值范圍.
的取值范圍.
【解析】第一問中,首先利用 在區間
在區間 上單調遞增,則
上單調遞增,則 在區間
在區間 上恒成立,然后分離參數法得到
上恒成立,然后分離參數法得到 ,進而得到范圍;第二問中,在區間
,進而得到范圍;第二問中,在區間 上,函數
上,函數 的圖象恒在曲線
的圖象恒在曲線 下方等價于
下方等價于 在區間
在區間 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在區間
在區間 上單調遞增,
上單調遞增,
則 在區間
在區間 上恒成立. …………3分
上恒成立. …………3分
即 ,而當
,而當 時,
時, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令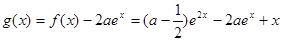 ,定義域為
,定義域為 .
.
在區間 上,函數
上,函數 的圖象恒在曲線
的圖象恒在曲線 下方等價于
下方等價于 在區間
在區間 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得極值點
,得極值點 ,
, ,
,
當 ,即
,即 時,在(
時,在( ,+∞)上有
,+∞)上有 ,此時
,此時 在區間
在區間 上是增函數,并且在該區間上有
上是增函數,并且在該區間上有 ,不合題意;
,不合題意;
當 ,即
,即 時,同理可知,
時,同理可知, 在區間
在區間 上遞增,
上遞增,
有 ,也不合題意;
…………11分
,也不合題意;
…………11分
② 若 ,則有
,則有 ,此時在區間
,此時在區間 上恒有
上恒有 ,從而
,從而 在區間
在區間 上是減函數;
上是減函數;
要使 在此區間上恒成立,只須滿足
在此區間上恒成立,只須滿足
 ,
,
由此求得 的范圍是
的范圍是 . …………13分
. …………13分
綜合①②可知,當 時,函數
時,函數 的圖象恒在直線
的圖象恒在直線 下方.
下方.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com