
題目列表(包括答案和解析)


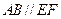

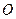
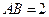

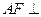 平面
平面 ;
;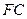 的中點為
的中點為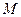 ,求證:
,求證: 平面
平面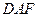 ;
; 的體積.
的體積.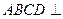 平面
平面 ;
; 的平面角的正切值.
的平面角的正切值.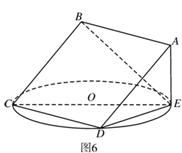
| PC |
| PA |
| PB |
| AP |
| AB |
| AQ |
| AC |
| 1 |
| m |
| 1 |
| n |

一、填空題:
1.試題.files/image244.gif) 2.
2. 試題.files/image246.gif) 3.
3.試題.files/image248.gif) 4.12
4.12試題.files/image250.gif) 5.
5.試題.files/image252.gif) 6.11 7.
6.11 7.試題.files/image254.gif) 8.2009
9.4個 10.①②
8.2009
9.4個 10.①②
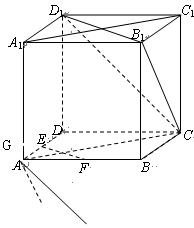
11.解: 試題.files/image256.gif) 。因為△ABC的面積為1,
。因為△ABC的面積為1, 試題.files/image084.gif) ,所以,△ABE的面積為
,所以,△ABE的面積為試題.files/image258.gif) ,因為D是AB的中點,所以, △BDE的面積為
,因為D是AB的中點,所以, △BDE的面積為試題.files/image260.gif) ,因為
,因為試題.files/image082.gif) ,所以△BDF的面積為
,所以△BDF的面積為試題.files/image262.gif) ,當且僅當
,當且僅當試題.files/image264.gif) 時,取得最大值。
時,取得最大值。
二、選擇題:
12.B 13.C 14.D 15.D
三、解答題:
16.解:(Ⅰ)因為試題.files/image133.gif) 點的坐標為
點的坐標為試題.files/image142.gif) ,根據三角函數定義可知
,根據三角函數定義可知試題.files/image267.gif) ,
,試題.files/image269.gif) ,
,試題.files/image271.gif) ,
2分
,
2分
所以試題.files/image273.gif) 4分
4分
(Ⅱ)因為三角形試題.files/image144.gif) 為正三角形,所以
為正三角形,所以試題.files/image275.gif) ,
,試題.files/image277.gif) ,
,試題.files/image279.gif) ,
5分
,
5分
所以試題.files/image281.gif)
試題.files/image283.gif) 8分
8分
所以試題.files/image285.gif)
試題.files/image287.gif) 。
11分
。
11分
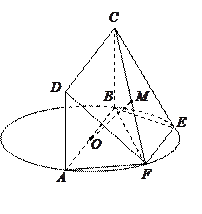
17.解:方法一:(I)證明:連結OC,因為試題.files/image289.gif) 所以
所以試題.files/image291.gif)
又試題.files/image293.gif) 所以
所以試題.files/image295.gif) ,
2分
,
2分
在試題.files/image297.gif) 中,由已知可得
中,由已知可得試題.files/image299.gif) 而
而試題.files/image301.gif)
所以試題.files/image303.gif) 所以
所以試題.files/image305.gif) 即
即試題.files/image307.gif) ,
,
而試題.files/image309.gif) 所以
所以試題.files/image164.gif) 平面
平面試題.files/image312.gif) 。
4分
。
4分
(II)解:取AC的中點M,連結OM、ME、OE,由E為BC的中點知試題.files/image314.gif)
所以直線OE與EM所成的銳角就是異面直線AB與CD所成的角, 5分
在試題.files/image316.gif) 中,
中,試題.files/image318.gif) 因為
因為試題.files/image320.gif) 是直角
是直角試題.files/image297.gif) 斜邊AC上的中線,所以
斜邊AC上的中線,所以試題.files/image323.gif) 所以
所以試題.files/image325.gif) 所以異面直線AB與CD所成角的大小為
所以異面直線AB與CD所成角的大小為試題.files/image327.gif) 。
8分
。
8分
(III)解:設點E到平面ACD的距離為試題.files/image329.gif) ,因為
,因為試題.files/image331.gif)
9分
在試題.files/image333.gif) 中,
中,試題.files/image335.gif) 所以
所以試題.files/image337.gif)
而試題.files/image339.gif) 所以
所以試題.files/image341.gif) ,
,
所以點E到平面ACD的距離為試題.files/image343.gif) 。
12分
。
12分
方法二:(I)同方法一。
(II)解:以O為原點,如圖建立直角坐標系,則試題.files/image345.gif)
試題.files/image347.gif) ,設
,設試題.files/image349.gif) 的夾角為
的夾角為試題.files/image351.gif) ,則
,則試題.files/image353.gif) 所以異面直線AB與CD所成角的大小為
所以異面直線AB與CD所成角的大小為試題.files/image327.gif) 。
。
試題.files/image356.gif) (III)解:設平面ACD的法向量為
(III)解:設平面ACD的法向量為試題.files/image358.gif) 則
則
試題.files/image360.gif)
試題.files/image362.gif)
令試題.files/image364.gif) 得
得試題.files/image366.gif) 是平面ACD的一個法向量。又
是平面ACD的一個法向量。又 試題.files/image368.gif) 所以點E到平面ACD的距離
所以點E到平面ACD的距離 試題.files/image370.gif) 。
。
18.解:(Ⅰ)由年銷售量為試題.files/image179.gif) 件,按利潤的計算公式,有生產A、B兩產品的年利潤
件,按利潤的計算公式,有生產A、B兩產品的年利潤試題.files/image373.gif) 分別為:
分別為:
試題.files/image375.gif) 且
且試題.files/image377.gif) 2分
2分
試題.files/image379.gif)
所以試題.files/image381.gif) 5分
5分
(Ⅱ)因為試題.files/image383.gif) 所以
所以試題.files/image385.gif) 為增函數,
為增函數,
試題.files/image387.gif) ,所以
,所以試題.files/image389.gif) 時,生產A產品有最大利潤為
時,生產A產品有最大利潤為試題.files/image391.gif) (萬美元)
7分
(萬美元)
7分
又試題.files/image393.gif) ,所以
,所以試題.files/image395.gif) 時,生產B產品
時,生產B產品
有最大利潤為460(萬美元) 9分
現在我們研究生產哪種產品年利潤最大,為此,我們作差比較:
試題.files/image397.gif) 11分
11分
所以:當試題.files/image399.gif) 時,投資生產A產品200件可獲得最大年利潤;
時,投資生產A產品200件可獲得最大年利潤;
當試題.files/image401.gif) 時,生產A產品與生產B產品均可獲得最大年利潤;
時,生產A產品與生產B產品均可獲得最大年利潤;
當試題.files/image403.gif) 時,投資生產B產品100件可獲得最大年利潤。12分
時,投資生產B產品100件可獲得最大年利潤。12分
19.解:(1)當試題.files/image405.gif) 時,
時,試題.files/image407.gif) ,
,試題.files/image409.gif) 成立,所以
成立,所以試題.files/image189.gif) 是奇函數;
是奇函數;
3分
當試題.files/image412.gif) 時,
時,試題.files/image414.gif) ,這時
,這時試題.files/image416.gif) 所以
所以試題.files/image189.gif) 是非奇非偶函數;
6分
是非奇非偶函數;
6分
(2)當試題.files/image191.gif) 時,
時,試題.files/image419.gif) 設
設試題.files/image421.gif) 且
且試題.files/image423.gif) ,則
,則
試題.files/image425.gif) 9分
9分
當試題.files/image427.gif) 時,因為
時,因為試題.files/image427.gif) 且
且試題.files/image423.gif) ,所以
,所以試題.files/image430.gif)
所以試題.files/image432.gif) ,
,
試題.files/image434.gif) ,所以
,所以試題.files/image189.gif) 是區間
是區間試題.files/image437.gif) 的單調遞減函數。 12分
的單調遞減函數。 12分
同理可得試題.files/image189.gif) 是區間
是區間試題.files/image439.gif) 的單調遞增函數。
14分
的單調遞增函數。
14分
20.解:(Ⅰ)由拋物線試題.files/image210.gif) :
:試題.files/image442.gif) 知
知試題.files/image444.gif) ,設
,設試題.files/image446.gif) ,
,試題.files/image206.gif) 在
在試題.files/image210.gif) 上,且
上,且試題.files/image212.gif) ,所以
,所以試題.files/image451.gif) ,得
,得試題.files/image453.gif) ,代入
,代入試題.files/image442.gif) ,得
,得試題.files/image455.gif) ,
,
所以試題.files/image457.gif) 。
4分
。
4分
試題.files/image206.gif) 在
在試題.files/image208.gif) 上,由已知橢圓
上,由已知橢圓試題.files/image208.gif) 的半焦距
的半焦距試題.files/image462.gif) ,于是
,于是試題.files/image464.gif)
消去試題.files/image466.gif) 并整理得
并整理得 試題.files/image468.gif) , 解得
, 解得試題.files/image470.gif) (
(試題.files/image472.gif) 不合題意,舍去).
不合題意,舍去).
故橢圓試題.files/image208.gif) 的方程為
的方程為試題.files/image475.gif) 。 7分
。 7分
(另法:因為試題.files/image206.gif) 在
在試題.files/image208.gif) 上,
上,
所以試題.files/image477.gif) ,所以
,所以試題.files/image470.gif) ,以下略。)
,以下略。)
(Ⅱ)由試題.files/image480.gif) 得
得試題.files/image482.gif) ,所以點O到直線
,所以點O到直線試題.files/image484.gif) 的距離為
的距離為
試題.files/image486.gif) ,又
,又試題.files/image488.gif) ,
,
所以試題.files/image490.gif) ,
,
試題.files/image492.gif) 且
且試題.files/image494.gif) 。
10分
。
10分
下面視提出問題的質量而定:
如問題一:當試題.files/image219.gif) 面積為
面積為試題.files/image496.gif) 時,求直線
時,求直線試題.files/image484.gif) 的方程。(
的方程。(試題.files/image499.gif) ) 得2分
) 得2分
問題二:當試題.files/image219.gif) 面積取最大值時,求直線
面積取最大值時,求直線試題.files/image484.gif) 的方程。(
的方程。(試題.files/image501.gif) ) 得4分
) 得4分
21.解:(1)
試題.files/image232.gif)
2
3
35
100
試題.files/image234.gif)
97
94
3
1
4分
(2)試題.files/image503.gif) 由題意知數列
由題意知數列試題.files/image222.gif) 的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,
6分
的前34項成首項為100,公差為-3的等差數列,從第35項開始,奇數項均為3,偶數項均為1,
6分
從而試題.files/image236.gif) =
=試題.files/image506.gif) 8分
8分
=試題.files/image508.gif) 。
10分
。
10分
(3)當試題.files/image240.gif) 時,因為
時,因為試題.files/image511.gif) ,
,
所以試題.files/image513.gif) 12分
12分
當試題.files/image515.gif) 時,
時,
試題.files/image517.gif)
試題.files/image519.gif)
試題.files/image521.gif)
因為試題.files/image240.gif) ,所以
,所以試題.files/image524.gif) ,
14分
,
14分
當試題.files/image526.gif) 時,
時,
試題.files/image528.gif)
所以試題.files/image242.gif) 。
16分
。
16分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com