
題目列表(包括答案和解析)
數(shù)列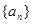 ,滿足
,滿足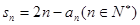
(1)求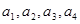 ,并猜想通項公式
,并猜想通項公式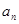 。
。
(2)用數(shù)學歸納法證明(1)中的猜想。
【解析】本試題主要考查了數(shù)列的通項公式求解,并用數(shù)學歸納法加以證明。第一問利用遞推關(guān)系式得到 ,
,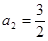 ,
,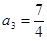 ,
,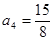 ,并猜想通項公式
,并猜想通項公式
第二問中,用數(shù)學歸納法證明(1)中的猜想。
①對n=1, 等式成立。
等式成立。
②假設(shè)n=k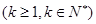 時,
時,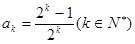 成立,
成立,
那么當n=k+1時,
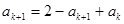 ,所以當n=k+1時結(jié)論成立可證。
,所以當n=k+1時結(jié)論成立可證。
數(shù)列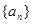 ,滿足
,滿足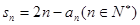
(1) ,
,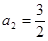 ,
,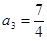 ,
,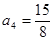 并猜想通項公
并猜想通項公 。 …4分
。 …4分
(2)用數(shù)學歸納法證明(1)中的猜想。①對n=1, 等式成立。 …5分
等式成立。 …5分
②假設(shè)n=k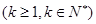 時,
時,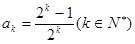 成立,
成立,
那么當n=k+1時,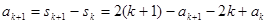
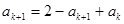 ,
……9分
,
……9分
所以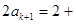
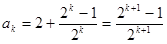
所以當n=k+1時結(jié)論成立 ……11分
由①②知,猜想對一切自然數(shù)n 均成立
均成立
(1)當n=1時,S1=a1顯然成立;
(2)假設(shè)當n=k時,公式成立,即Sk=ka1+![]() ,
,
當n=k+1時,Sk+1 =a1+a2+…+ak+ak+1 =a1+(a1+d)+(a1+2d)+…+[a1+(k-1)d]+(a1+kd)=(k+1)a1+(d+2d+…+kd)
=(k+1)a1+![]() d=(k+1)a1+
d=(k+1)a1+![]() d,
d,
∴n=k+1時公式成立.
由(1)(2)知,對n∈N*時,公式都成立.
以上證明錯誤的是( )
A.當n取第一個值1時,證明不對
B.歸納假設(shè)的寫法不對
C.從n=k到n=k+1時的推理中未用歸納假設(shè)
D.從n=k到n=k+1時的推理有錯誤
已知 是等差數(shù)列,其前n項和為Sn,
是等差數(shù)列,其前n項和為Sn, 是等比數(shù)列,且
是等比數(shù)列,且 ,
, .
.
(Ⅰ)求數(shù)列 與
與 的通項公式;
的通項公式;
(Ⅱ)記 ,
, ,證明
,證明 (
( ).
).
【解析】(1)設(shè)等差數(shù)列 的公差為d,等比數(shù)列
的公差為d,等比數(shù)列 的公比為q.
的公比為q.
由 ,得
,得 ,
, ,
, .
.
由條件,得方程組 ,解得
,解得
所以 ,
, ,
, .
.
(2)證明:(方法一)
由(1)得
 ①
①
 ②
②
由②-①得



而
故 ,
,
(方法二:數(shù)學歸納法)
① 當n=1時,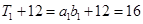 ,
, ,故等式成立.
,故等式成立.
② 假設(shè)當n=k時等式成立,即 ,則當n=k+1時,有:
,則當n=k+1時,有:






即 ,因此n=k+1時等式也成立
,因此n=k+1時等式也成立
由①和②,可知對任意 ,
, 成立.
成立.
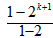 =2k+1-1,所以n=k+1時等式也成立,
=2k+1-1,所以n=k+1時等式也成立,[ ]
| AnAn+1 |
| BnCn |
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com