
題目列表(包括答案和解析)
函數 是定義在
是定義在 上的奇函數,且
上的奇函數,且 。
。
(1)求實數a,b,并確定函數 的解析式;
的解析式;
(2)判斷 在(-1,1)上的單調性,并用定義證明你的結論;
在(-1,1)上的單調性,并用定義證明你的結論;
(3)寫出 的單調減區間,并判斷
的單調減區間,并判斷 有無最大值或最小值?如有,寫出最大值或最小值。(本小問不需要說明理由)
有無最大值或最小值?如有,寫出最大值或最小值。(本小問不需要說明理由)
【解析】本試題主要考查了函數的解析式和奇偶性和單調性的綜合運用。第一問中,利用函數 是定義在
是定義在 上的奇函數,且
上的奇函數,且 。
。
解得 ,
,
(2)中,利用單調性的定義,作差變形判定可得單調遞增函數。
(3)中,由2知,單調減區間為 ,并由此得到當,x=-1時,
,并由此得到當,x=-1時, ,當x=1時,
,當x=1時,
解:(1) 是奇函數,
是奇函數, 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函數。…………………………………………8分
在(-1,1)上是增函數。…………………………………………8分
(3)單調減區間為 …………………………………………10分
…………………………………………10分
當,x=-1時, ,當x=1時,
,當x=1時, 。
。
給出下列四個命題:
(1)函數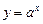 (
(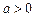 且
且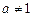 )與函數
)與函數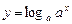 (
(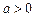 且
且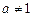 )的定義域相同;
)的定義域相同;
(2)函數 與
與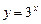 的值域相同;
的值域相同;
(3)函數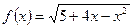 的單調遞增區間為
的單調遞增區間為 ;
;
其中正確命題的序號是__________(把你認為正確的命題序號都填上)。
給出下列四個命題:
(1)函數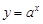 (
( 且
且 )與函數
)與函數 (
( 且
且 )的定義域相同;
)的定義域相同;
(2)函數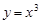 與
與 的值域相同;
的值域相同;
(3)函數 的單調遞增區間為
的單調遞增區間為 ;
;
(4)函數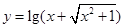 是奇函數。
是奇函數。
其中正確命題的序號是__________(把你認為正確的命題序號都填上)。
給出下列四個命題:
(1)函數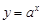 (
( 且
且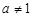 )與函數
)與函數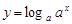 (
( 且
且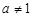 )的定義域相同;
)的定義域相同;
(2)函數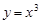 與
與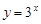 的值域相同;
的值域相同;
(3)函數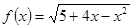 的單調遞增區間為
的單調遞增區間為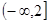 ;
;
其中正確命題的序號是__________(把你認為正確的命題序號都填上)。
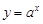 (
(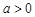 且
且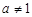 )與函數
)與函數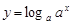 (
(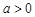 且
且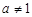 )的定義域相同;
)的定義域相同;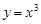 與
與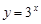 的值域相同;
的值域相同;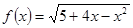 的單調遞增區間為
的單調遞增區間為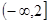 ;
;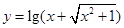 是奇函數。
是奇函數。一、選擇題:
1―5:ACCCB 6―10:CDACD 11―12:BC
二、填空題:
13.2 14. 15.5
16.①
15.5
16.① ②球的體積函數的導數等于球的表面積函數
②球的體積函數的導數等于球的表面積函數
三、解答題:
17.(本小題滿分12分)
解:(I) ……………………2分
……………………2分
 ……………………4分
……………………4分
 ……………………………………………………………………5分
……………………………………………………………………5分
(II) 、B均為銳角且B<A
、B均為銳角且B<A
又C為鈍角
∴最短邊為b……………………………………………………7分
由 ,解得
,解得 ………………………………9分
………………………………9分
又 …………………………12分
…………………………12分
18.(本小題滿分12分)
解:(I)

 ………………………………3分
………………………………3分
故 …………………………………………………4分
…………………………………………………4分
(II)令 .
.
若 時,當
時,當 時,函數
時,函數
 …………………………………………………………6分
…………………………………………………………6分
若 時,當
時,當 時,函數
時,函數
 …………………………………………………………8分
…………………………………………………………8分
(III)由
確定 單調遞增的正值區間是
單調遞增的正值區間是 ;
;
由
確定 單調遞減的正值區間是
單調遞減的正值區間是 ;………10分
;………10分
綜上,當 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為 .
.
當 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為 .……12分
.……12分
注:①
 的這些
的這些
等價形式中,以 最好用. 因為復合函數
最好用. 因為復合函數
 的中間變量
的中間變量 是增函數,對求
是增函數,對求 的單調區間來說,
的單調區間來說,
只看外層函數 的單調性即可.否則,利用
的單調性即可.否則,利用 的其它形
的其它形
式,例如 求單調區間是非常容易出錯的. 同學們可以嘗試做一
求單調區間是非常容易出錯的. 同學們可以嘗試做一
下 的其它形式,認真體會,比較優劣!
的其它形式,認真體會,比較優劣!
②今后遇到求類似 的單調區間問題,應首先通過誘導公式將
的單調區間問題,應首先通過誘導公式將 轉化為標準形
轉化為標準形
式: (其中A>0,ω>0),然后再行求
(其中A>0,ω>0),然后再行求
解,保險系數就大了.
19.(本小題滿分12分)
解:(I)由已知 ……………………1分
……………………1分
 …………3分
…………3分
由已知
∴公差d=1…………………………………………………………4分

 ……………………………………………………6分
……………………………………………………6分
(II)設 …………………………7分
…………………………7分
當 時,
時, 是k的增函數,
是k的增函數, 也是k的增函數.
也是k的增函數.
 ………………………………10分
………………………………10分
又
 不存在
不存在 ,使
,使 …………………………………12分
…………………………………12分
20.(本小題滿分12分)
解: 恒成立
恒成立
只需 小于
小于 的最小值…………………………………………2分
的最小值…………………………………………2分
而當 時,
時, ≥3……………………………………………4分
≥3……………………………………………4分
 ……………………………………………………6分
……………………………………………………6分
 存在極大值與極小值
存在極大值與極小值
 有兩個不等的實根…………………………8分
有兩個不等的實根…………………………8分

 或
或 …………………………………………………………10分
…………………………………………………………10分
要使“P且 Q”為真,只需
Q”為真,只需
故m的取值范圍為[2,6].…………………………………………………12分
21.(本小題滿分12分)
解:設此工廠應分別生產甲、乙兩種產品x噸、y噸,獲得利潤z萬元………1分
依題意可得約束條件: