
題目列表(包括答案和解析)
函數(shù) 是定義在
是定義在 上的奇函數(shù),且
上的奇函數(shù),且 。
。
(1)求實(shí)數(shù)a,b,并確定函數(shù) 的解析式;
的解析式;
(2)判斷 在(-1,1)上的單調(diào)性,并用定義證明你的結(jié)論;
在(-1,1)上的單調(diào)性,并用定義證明你的結(jié)論;
(3)寫(xiě)出 的單調(diào)減區(qū)間,并判斷
的單調(diào)減區(qū)間,并判斷 有無(wú)最大值或最小值?如有,寫(xiě)出最大值或最小值。(本小問(wèn)不需要說(shuō)明理由)
有無(wú)最大值或最小值?如有,寫(xiě)出最大值或最小值。(本小問(wèn)不需要說(shuō)明理由)
【解析】本試題主要考查了函數(shù)的解析式和奇偶性和單調(diào)性的綜合運(yùn)用。第一問(wèn)中,利用函數(shù) 是定義在
是定義在 上的奇函數(shù),且
上的奇函數(shù),且 。
。
解得 ,
,
(2)中,利用單調(diào)性的定義,作差變形判定可得單調(diào)遞增函數(shù)。
(3)中,由2知,單調(diào)減區(qū)間為 ,并由此得到當(dāng),x=-1時(shí),
,并由此得到當(dāng),x=-1時(shí), ,當(dāng)x=1時(shí),
,當(dāng)x=1時(shí),
解:(1) 是奇函數(shù),
是奇函數(shù), 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函數(shù)。…………………………………………8分
在(-1,1)上是增函數(shù)。…………………………………………8分
(3)單調(diào)減區(qū)間為 …………………………………………10分
…………………………………………10分
當(dāng),x=-1時(shí), ,當(dāng)x=1時(shí),
,當(dāng)x=1時(shí), 。
。
已知函數(shù) .(
.( )
)
(1)若 在區(qū)間
在區(qū)間 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù) 的取值范圍;
的取值范圍;
(2)若在區(qū)間 上,函數(shù)
上,函數(shù) 的圖象恒在曲線
的圖象恒在曲線 下方,求
下方,求 的取值范圍.
的取值范圍.
【解析】第一問(wèn)中,首先利用 在區(qū)間
在區(qū)間 上單調(diào)遞增,則
上單調(diào)遞增,則 在區(qū)間
在區(qū)間 上恒成立,然后分離參數(shù)法得到
上恒成立,然后分離參數(shù)法得到 ,進(jìn)而得到范圍;第二問(wèn)中,在區(qū)間
,進(jìn)而得到范圍;第二問(wèn)中,在區(qū)間 上,函數(shù)
上,函數(shù) 的圖象恒在曲線
的圖象恒在曲線 下方等價(jià)于
下方等價(jià)于 在區(qū)間
在區(qū)間 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在區(qū)間
在區(qū)間 上單調(diào)遞增,
上單調(diào)遞增,
則 在區(qū)間
在區(qū)間 上恒成立. …………3分
上恒成立. …………3分
即 ,而當(dāng)
,而當(dāng) 時(shí),
時(shí), ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令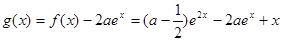 ,定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061918574873515193/SYS201206191859562664899842_ST.files/image016.png">.
,定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061918574873515193/SYS201206191859562664899842_ST.files/image016.png">.
在區(qū)間 上,函數(shù)
上,函數(shù) 的圖象恒在曲線
的圖象恒在曲線 下方等價(jià)于
下方等價(jià)于 在區(qū)間
在區(qū)間 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得極值點(diǎn)
,得極值點(diǎn) ,
, ,
,
當(dāng) ,即
,即 時(shí),在(
時(shí),在( ,+∞)上有
,+∞)上有 ,此時(shí)
,此時(shí) 在區(qū)間
在區(qū)間 上是增函數(shù),并且在該區(qū)間上有
上是增函數(shù),并且在該區(qū)間上有 ,不合題意;
,不合題意;
當(dāng) ,即
,即 時(shí),同理可知,
時(shí),同理可知, 在區(qū)間
在區(qū)間 上遞增,
上遞增,
有 ,也不合題意;
…………11分
,也不合題意;
…………11分
② 若 ,則有
,則有 ,此時(shí)在區(qū)間
,此時(shí)在區(qū)間 上恒有
上恒有 ,從而
,從而 在區(qū)間
在區(qū)間 上是減函數(shù);
上是減函數(shù);
要使 在此區(qū)間上恒成立,只須滿足
在此區(qū)間上恒成立,只須滿足
 ,
,
由此求得 的范圍是
的范圍是 . …………13分
. …………13分
綜合①②可知,當(dāng) 時(shí),函數(shù)
時(shí),函數(shù) 的圖象恒在直線
的圖象恒在直線 下方.
下方.
已知 ,(其中
,(其中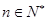 )
)
⑴求 及
及 ;
;
⑵試比較 與
與 的大小,并說(shuō)明理由.
的大小,并說(shuō)明理由.
【解析】第一問(wèn)中取 ,則
,則 ;
…………1分
;
…………1分
對(duì)等式兩邊求導(dǎo),得
取 ,則
,則 得到結(jié)論
得到結(jié)論
第二問(wèn)中,要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,歸納猜想可得結(jié)論當(dāng)
的大小,歸納猜想可得結(jié)論當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
猜想:當(dāng) 時(shí),
時(shí), 運(yùn)用數(shù)學(xué)歸納法證明即可。
運(yùn)用數(shù)學(xué)歸納法證明即可。
解:⑴取 ,則
,則 ;
…………1分
;
…………1分
對(duì)等式兩邊求導(dǎo),得 ,
,
取 ,則
,則 。 …………4分
。 …………4分
⑵要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,
的大小,
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
…………6分
;
…………6分
猜想:當(dāng) 時(shí),
時(shí), ,下面用數(shù)學(xué)歸納法證明:
,下面用數(shù)學(xué)歸納法證明:
由上述過(guò)程可知, 時(shí)結(jié)論成立,
時(shí)結(jié)論成立,
假設(shè)當(dāng) 時(shí)結(jié)論成立,即
時(shí)結(jié)論成立,即 ,
,
當(dāng) 時(shí),
時(shí),
而
∴
即 時(shí)結(jié)論也成立,
時(shí)結(jié)論也成立,
∴當(dāng) 時(shí),
時(shí), 成立。
…………11分
成立。
…………11分
綜上得,當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí),
已知函數(shù) ,
,
(Ⅰ)求函數(shù) 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(Ⅱ)令函數(shù) (
( ),求函數(shù)
),求函數(shù) 的最大值的表達(dá)式
的最大值的表達(dá)式 ;
;
【解析】第一問(wèn)中利用令 ,
, ,
,
∴ ,
,
第二問(wèn)中, =
=
=
= 令
令 ,
,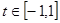 ,則
,則 借助于二次函數(shù)分類討論得到最值。
借助于二次函數(shù)分類討論得到最值。
(Ⅰ)解:令 ,
, ,
,
∴ ,
,
∴ 的單調(diào)遞減區(qū)間為:
的單調(diào)遞減區(qū)間為:
 …………………4分
…………………4分
(Ⅱ)解: =
=
=
=
令 ,
,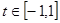 ,則
,則 ……………………4分
……………………4分
對(duì)稱軸
① 當(dāng) 即
即 時(shí),
時(shí), =
= ……………1分
……………1分
② 當(dāng) 即
即 時(shí),
時(shí), =
= ……………1分
……………1分
③ 當(dāng) 即
即 時(shí),
時(shí), ……………1分
……………1分
綜上:
已知函數(shù) 的最小值為0,其中
的最小值為0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若對(duì)任意的 有
有 ≤
≤ 成立,求實(shí)數(shù)
成立,求實(shí)數(shù) 的最小值;
的最小值;
(Ⅲ)證明 (
( ).
).
【解析】(1)解:
 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118530600520067_ST.files/image010.png">
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118530600520067_ST.files/image010.png">

由 ,得
,得
當(dāng)x變化時(shí), ,
, 的變化情況如下表:
的變化情況如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
極小值 |
|
因此, 在
在 處取得最小值,故由題意
處取得最小值,故由題意 ,所以
,所以
(2)解:當(dāng) 時(shí),取
時(shí),取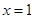 ,有
,有 ,故
,故 時(shí)不合題意.當(dāng)
時(shí)不合題意.當(dāng)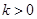 時(shí),令
時(shí),令 ,即
,即

令 ,得
,得
①當(dāng) 時(shí),
時(shí), ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上單調(diào)遞減.從而對(duì)于任意的
上單調(diào)遞減.從而對(duì)于任意的 ,總有
,總有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合題意.
符合題意.
②當(dāng) 時(shí),
時(shí), ,對(duì)于
,對(duì)于 ,
, ,故
,故 在
在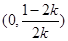 上單調(diào)遞增.因此當(dāng)取
上單調(diào)遞增.因此當(dāng)取 時(shí),
時(shí), ,即
,即 不成立.
不成立.
故 不合題意.
不合題意.
綜上,k的最小值為 .
.
(3)證明:當(dāng)n=1時(shí),不等式左邊= =右邊,所以不等式成立.
=右邊,所以不等式成立.
當(dāng) 時(shí),
時(shí),


在(2)中取 ,得
,得
 ,
,
從而

所以有





綜上,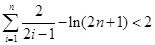 ,
,
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com