
題目列表(包括答案和解析)
若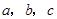 是不全相等的實數,求證:
是不全相等的實數,求證: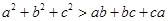 .
.
證明過程如下:
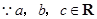 ,
,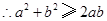 ,
,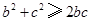 ,
,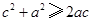 ,
,
又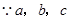 不全相等,
不全相等,
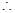 以上三式至少有一個“
以上三式至少有一個“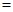 ”不成立,
”不成立,
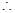 將以上三式相加得
將以上三式相加得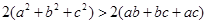 ,
,
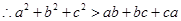 .
.
此證法是( )
A.分析法 B.綜合法 C.分析法與綜合法并用 D.反證法
若a,b,c是不全相等的實數,求證:a2+b2+c2>ab+bc+ca.
證明過程如下:
∵a、b、c∈R,∴a2+b2≥2ab,
b2+c2≥2bc,c2+a2≥2ac,
又∵a,b,c不全相等,
∴以上三式至少有一個“=”不成立,
∴將以上三式相加得2(a2+b2+c2)>2(ab+bc+ac),
∴a2+b2+c2>ab+bc![]() +ca.
+ca.
此證法是( )
(A)分析法 (B)綜合法
(C)分析法與綜合法并用 (D)反證法
數列 首項
首項 ,前
,前 項和
項和 滿足等式
滿足等式 (常數
(常數 ,
, ……)
……)
(1)求證: 為等比數列;
為等比數列;
(2)設數列 的公比為
的公比為 ,作數列
,作數列 使
使 (
( ……),求數列
……),求數列 的通項公式.
的通項公式.
(3)設 ,求數列
,求數列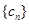 的前
的前 項和
項和 .
.
【解析】第一問利用由 得
得
兩式相減得
故 時,
時,
從而 又
又 即
即 ,而
,而
從而 故
故
第二問中,
 又
又 故
故 為等比數列,通項公式為
為等比數列,通項公式為
第三問中,
 兩邊同乘以
兩邊同乘以
利用錯位相減法得到和。
(1)由 得
得
兩式相減得
故 時,
時,
從而 ………………3分
………………3分
又 即
即 ,而
,而
從而 故
故
 對任意
對任意 ,
, 為常數,即
為常數,即 為等比數列………………5分
為等比數列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 為等比數列,通項公式為
為等比數列,通項公式為 ………………9分
………………9分
(3)
 兩邊同乘以
兩邊同乘以
 ………………11分
………………11分
兩式相減得

某電視臺“挑戰主持人”節目的挑戰者闖第一關需要回答3個問題,其中前兩個問
題回答正確各得10分,回答不正確各得0分,第三題回答正確得20分,回答不正確得-10分,總得分不少于30分即可過關.如果一位挑戰者回答前兩題正確的概率都是![]() ,回答第三題正確的概率為
,回答第三題正確的概率為![]() ,且各題回答正確與否相互之間沒有影響.記這位挑戰者回答這三個問題的總得分為
,且各題回答正確與否相互之間沒有影響.記這位挑戰者回答這三個問題的總得分為![]() 。
。
(1)求這位挑戰者過關的概率有多大; (2)求![]() 的概率分布和數學期望。
的概率分布和數學期望。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com