題目列表(包括答案和解析)
設(shè)f(x)是定義在[－1，1]上的奇函數(shù)，且對任意的實(shí)數(shù)a，b∈[－1，1]，當(dāng)a＋b≠0時(shí)，都有
＞0．
(1)若a＞b，試比較f(a)與f(b)的大小；
(2)解不等式f(x－
)＜f(x－
)；
(3)如果g(x)＝f(x－c)和h(x)＝f(x－c2)這兩個(gè)函數(shù)的定義域的交集是空集，求c的取值范圍．
設(shè)函數(shù)f(x)＝x2－mlnx，g(x)＝x2－x＋a.
(1)當(dāng)a＝0時(shí)，f(x)≥g(x)在(1，＋∞),上恒成立，求實(shí)數(shù)m的取值范圍；
(2)當(dāng)m＝2時(shí)，若函數(shù)h(x)=f(x)－g(x)在[1,3]上恰有兩個(gè)不同的零點(diǎn)，求實(shí)數(shù)a的取值范圍．
如圖，在平面
直角坐標(biāo)系中，方程為x2＋y2＋Dx＋Ey＋F＝0的圓M的內(nèi)接四邊形ABCD的對角線AC和BD互相垂直，且AC和BD分別在x軸和y軸上.
(1)求證：F＜0；
(2)若四邊形ABCD的面積為8，對角線AC的長為2，且
＝0，求D2＋E2－4F的值；
(3)設(shè)四邊形ABCD的一條邊CD的中點(diǎn)為G，OH⊥AB且垂足為H.試用平面解析幾何的研究方法判斷點(diǎn)O、G、H是否共線，并說明理由.
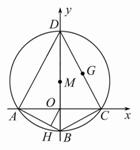
如圖，在平面直角坐標(biāo)系中，方程為x2＋y2＋Dx＋Ey＋F＝0的圓M的內(nèi)接四邊形ABCD的對角線AC和BD互相垂直，且AC和BD分別在x軸和y軸上．
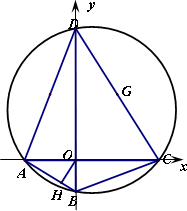
(1)求證：F＜0；
(2)若四邊形ABCD的面積為8，對角線AC的長為2，且
·
＝0，求D2＋E2－4F的值；
(3)設(shè)四邊形ABCD的一條邊CD的中點(diǎn)為G，OH⊥AB且垂足為H．試用平面解析幾何的研究方法判斷點(diǎn)O、G、H是否共線，并說明理由．
ABAACBBCDB
155
0
17、解：（Ⅰ）
（Ⅱ）
18、解: (I) 由于在閉區(qū)間[0，7]上，只有
，故
．若
是奇函數(shù)，則
，矛盾．所以，不是奇函數(shù)．
由
, 從而知函數(shù)
是以
為周期的函數(shù)．
若是偶函數(shù)，則
．又
，從而
．
由于對任意的
（3，7]上，
，又函數(shù)的圖象的關(guān)于
對稱，所以對區(qū)間[7，11）上的任意
均有．所以，
，這與前面的結(jié)論矛盾．
所以，函數(shù)是非奇非偶函數(shù)．
(II) 由第(I)小題的解答，我們知道
在區(qū)間（0，10）有且只有兩個(gè)解，并且．由于函數(shù)是以為周期的函數(shù)，故
．所以在區(qū)間[－2000,2000]上，方程共有
個(gè)解．
在區(qū)間[2000,2010]上，方程有且只有兩個(gè)解．因?yàn)?/p>
，
所以，在區(qū)間[2000,2005]上，方程有且只有兩個(gè)解．
在區(qū)間[－2010,－2000]上，方程有且只有兩個(gè)解．因?yàn)?/p>
，
所以，在區(qū)間[－2005,－2000]上，方程無解．
綜上所述，方程在[－2005,2005]上共有802個(gè)解.
19、[解]（1）
（2）方程
的解分別是
和
，由于
在
和
上單調(diào)遞減，在
和
上單調(diào)遞增，因此
.
由于
.
（3）[解法一] 當(dāng)
時(shí)，
.
，
. 又
，
①
當(dāng)
，即
時(shí)，取
，
.
，
則
.
②
當(dāng)
，即
時(shí)，取
， ＝
.
由 ①、②可知，當(dāng)
時(shí)，
，.
因此，在區(qū)間
上，
的圖像位于函數(shù)圖像的上方.
[解法二] 當(dāng)時(shí)，.
由
得
，
令 
，解得 
或
，
在區(qū)間上，當(dāng)時(shí)，
的圖像與函數(shù)的圖像只交于一點(diǎn)
； 當(dāng)時(shí)，
的圖像與函數(shù)的圖像沒有交點(diǎn).
如圖可知，由于直線過點(diǎn)
，當(dāng)時(shí)，直線是由直線繞點(diǎn)逆時(shí)針方向旋轉(zhuǎn)得到. 因此，在區(qū)間上，的圖像位于函數(shù)圖像的上方.
20、解：(Ⅰ)設(shè)函數(shù)
的圖象上任意一點(diǎn)
關(guān)于原點(diǎn)的對稱點(diǎn)為
，則
∵點(diǎn)
在函數(shù)
的圖象上
∴
(Ⅱ)由
當(dāng)
時(shí)，
，此時(shí)不等式無解
當(dāng)
時(shí)，
，解得
因此，原不等式的解集為
（Ⅲ）
①
②
?）
?）
21、解：（I）∵
，
∴要使
有意義，必須
且
，即
∵
，且
……① ∴的取值范圍是
。
由①得：
，∴
，
。
（II）由題意知
即為函數(shù)
，的最大值，
∵直線
是拋物線的對稱軸，∴可分以下幾種情況進(jìn)行討論：
（1）當(dāng)
時(shí)，函數(shù)
，的圖象是開口向上的拋物線的一段，
由
知在上單調(diào)遞增，故
；
（2）當(dāng)
時(shí)，
，，有=2；
（3）當(dāng)
時(shí)，，函數(shù)，的圖象是開口向下的拋物線的一段，
若
即
時(shí)，
，
若
即
時(shí)，
，
若
即
時(shí)，。
綜上所述，有=
。
（III）當(dāng)
時(shí)，
；
當(dāng)
時(shí)，
，
，∴
，
，故當(dāng)
時(shí)，
；
當(dāng)時(shí)，
，由
知：
，故
；
當(dāng)時(shí)，
，故
或
，從而有
或
，
要使，必須有
，
，即
，
此時(shí)，。
綜上所述，滿足
的所有實(shí)數(shù)a為：或。
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com