
題目列表(包括答案和解析)
已知x=-1是![]() 的一個(gè)極值點(diǎn)
的一個(gè)極值點(diǎn)
(1)求![]() 的值;
的值;
(2)求函數(shù)![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(3)設(shè)![]() ,試問過點(diǎn)(2,5)可作多少條直線與曲線y=g(x)相切?請(qǐng)說明理由。
,試問過點(diǎn)(2,5)可作多少條直線與曲線y=g(x)相切?請(qǐng)說明理由。
已知下列四個(gè)命題:
①若函數(shù)y=f(x)在x0處的導(dǎo)數(shù)![]() (x0)=0,則它在x=x0處有極值;
(x0)=0,則它在x=x0處有極值;
②若不論m為何值,直線y=mx+1均與曲線![]() 有公共點(diǎn),則b≥1;
有公共點(diǎn),則b≥1;
③若x、y、z∈R+,a=x+![]() ,b=y(tǒng)+
,b=y(tǒng)+![]() ,c=z+
,c=z+![]() ,則a、b、c中至少有一個(gè)不小于2;
,則a、b、c中至少有一個(gè)不小于2;
④若命題“存在x∈R,使得|x-a|+|x+1|≤2”是假命題,則|a+1|>2;
以上四個(gè)命題正確的是________(填入相應(yīng)序號(hào)).
已知函數(shù)f(x)=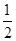 m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)當(dāng)m= 時(shí),求函數(shù)f(x)在區(qū)間[1,3]上的極小值;
時(shí),求函數(shù)f(x)在區(qū)間[1,3]上的極小值;
(2)求證:函數(shù)f(x)存在單調(diào)遞減區(qū)間[a,b];
(3)是否存在實(shí)數(shù)m,使曲線C:y=f(x)在點(diǎn)P(1,1)處的切線l與曲線C有且只有一個(gè)公共點(diǎn)?若存在,求出實(shí)數(shù)m的值;若不存在,請(qǐng)說明理由.
 m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1. 時(shí),求函數(shù)f(x)在區(qū)間[1,3]上的極小值;
時(shí),求函數(shù)f(x)在區(qū)間[1,3]上的極小值;已知函數(shù)f(x)= m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)當(dāng)m= 時(shí),求函數(shù)f(x)在區(qū)間[1,3]上的極小值;
時(shí),求函數(shù)f(x)在區(qū)間[1,3]上的極小值;
(2)求證:函數(shù)f(x)存在單調(diào)遞減區(qū)間[a,b];
(3)是否存在實(shí)數(shù)m,使曲線C:y=f(x)在點(diǎn)P(1,1)處的切線l與曲線C有且只有一個(gè)公共點(diǎn)?若存在,求出實(shí)數(shù)m的值;若不存在,請(qǐng)說明理由.
2008.11
一、填空題
⒈年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image120.gif) ⒉
⒉年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image122.gif) ⒊-i ⒋
⒊-i ⒋年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image124.gif) ⒌
⒌年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image126.gif)
⒍年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image128.gif) ⒎
⒎年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image130.gif) ⒏
⒏年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image132.gif) ⒐
⒐年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image134.gif) ⒑
⒑年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image136.gif)
⒒14
⒓年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image138.gif) ⒔
⒔年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image140.gif) ⒕m>
⒕m>年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image142.gif)
二、解答題
⒖解:(Ⅰ) 年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image076.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image144.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image146.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image148.gif) ……(4分)
……(4分)
∵函數(shù)年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image150.gif) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image152.gif) ,
,年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image154.gif)
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image156.gif) ,∴
,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image158.gif) ,
,年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image154.gif)
∴函數(shù)f(x)的單調(diào)遞增區(qū)間為年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image160.gif) ,
,年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image154.gif) ……(8分)
……(8分)
(Ⅱ)當(dāng)年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image078.gif) 時(shí),
時(shí),年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image162.gif) ,∴
,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image164.gif)
∴函數(shù)f(x)的值域?yàn)?sub>年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image166.gif) ……(14分)
……(14分)
⒗解:(Ⅰ) ∵DC⊥平面ABC,EB⊥平面ABC
∴DC//EB,又∵DC年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image168.gif) 平面ABE,EB
平面ABE,EB年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image170.gif) 平面ABE,∴DC∥平面ABE……(4分)
平面ABE,∴DC∥平面ABE……(4分)
(Ⅱ)∵DC⊥平面ABC,∴DC⊥AF,又∵AF⊥BC,∴AF⊥平面BCDE……(8分)
(Ⅲ)由(2)知AF⊥平面BCDE,∴AF⊥EF,在三角形DEF中,由計(jì)算知DF⊥EF,
∴EF⊥平面AFD,又EF年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image170.gif) 平面AFE,∴平面AFD⊥平面AFE.……(14分)
平面AFE,∴平面AFD⊥平面AFE.……(14分)
⒘解:根據(jù)題意得,BC=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image086.gif) km,BD=
km,BD=
設(shè)∠ACD=α,∠CDB=β
在△CDB中,由余弦定理得
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image172.gif) ,所以
,所以年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image174.gif)
于是年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image176.gif) …………(7分)
…………(7分)
在△ACD中,由正弦定理得
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image178.gif)
答:此人還得走年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image180.gif) km到達(dá)A城……(14分)
km到達(dá)A城……(14分)
⒙解:(1) 因x=-1是年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image088.gif) 的一個(gè)極值點(diǎn)
的一個(gè)極值點(diǎn)
∴ 年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image182.gif)
即 2+b-1=0
∴b= -1,經(jīng)檢驗(yàn),適合題意,所以b= -1.……(5分)
(2) 年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image184.gif)
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image184.gif) >0
>0
∴ 年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image186.gif) >0
>0
∴x>年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image188.gif)
∴函數(shù)的單調(diào)增區(qū)間為年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image190.gif) ……(10分)
……(10分)
(3)對(duì)年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image093.gif) 時(shí),f(x)>c-4x恒成立
時(shí),f(x)>c-4x恒成立
∴即對(duì)年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image093.gif) 時(shí),f(x) +4x >c恒成立
時(shí),f(x) +4x >c恒成立
令年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image192.gif) =
=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image194.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image196.gif) =
=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image198.gif) =0
=0
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image200.gif) 或
或年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image202.gif) (舍)
(舍)
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image103.gif) 在
在年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image205.gif) 上單調(diào)遞減,在
上單調(diào)遞減,在年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image207.gif) 上單調(diào)遞增。
上單調(diào)遞增。
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image103.gif) 在x=
在x=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image209.gif) 時(shí)取最小值5-
時(shí)取最小值5-年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image211.gif)
∴C<5-年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image211.gif) ……………………………………(16分)
……………………………………(16分)
⒚解:(Ⅰ)∵年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image101.gif) 為偶函數(shù),∴
為偶函數(shù),∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image213.gif) ,∴
,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image215.gif) ,∴
,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image217.gif)
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image219.gif) ,∴函數(shù)
,∴函數(shù)年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image103.gif) 為奇函數(shù);……(4分)
為奇函數(shù);……(4分)
(Ⅱ)⑴由年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image222.gif) 得方程
得方程年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image224.gif) 有不等實(shí)根
有不等實(shí)根
∴△年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image226.gif) 及
及年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image228.gif) 得
得年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image230.gif) 即
即年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image232.gif)
又年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image101.gif) 的對(duì)稱軸
的對(duì)稱軸年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image234.gif)
故年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image101.gif) 在(-1,1)上是單調(diào)函數(shù)……………………………………………(10分)
在(-1,1)上是單調(diào)函數(shù)……………………………………………(10分)
⑵年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image236.gif) 是方程(*)的根,∴
是方程(*)的根,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image238.gif)
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image240.gif) ,同理
,同理年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image242.gif)
∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image244.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image246.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image248.gif)
同理年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image250.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image252.gif)
要使年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image113.gif) ,只需
,只需年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image254.gif) 即
即年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image256.gif) ,∴
,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image258.gif)
或年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image260.gif) 即
即年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image262.gif) ,解集為
,解集為年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image264.gif)
故年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image043.gif) 的取值范圍
的取值范圍年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image258.gif) ……………………(16分)
……………………(16分)
⒛(Ⅰ)證明:年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image267.gif) ,
,年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image269.gif)
由條件可得年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image271.gif) ,所以
,所以年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image273.gif) ……(4分)
……(4分)
(Ⅱ)解:因?yàn)閎n+1=(-1)n+1[an+1-3(n-1)+9]=(-1)n+1(年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image275.gif) an-2n+6)
an-2n+6)
=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image275.gif) (-1)n?(an-3n+9)=-
(-1)n?(an-3n+9)=-年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image275.gif) bn
bn
又b1=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image277.gif) ,所以
,所以
當(dāng)λ=-6時(shí),bn=0(n∈N+),此時(shí){bn}不是等比數(shù)列,
當(dāng)λ≠-6時(shí),b1=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image277.gif) ≠0,由上可知bn≠0,∴
≠0,由上可知bn≠0,∴年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image280.gif) (n∈N+).
(n∈N+).
故當(dāng)λ≠-6時(shí),數(shù)列{bn}是以-(λ+6)為首項(xiàng),-年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image275.gif) 為公比的等比數(shù)列.……(10分)
為公比的等比數(shù)列.……(10分)
(Ⅲ)由(Ⅱ)知,當(dāng)λ=-6,bn=0,Sn=0,不滿足題目要求.
∴λ≠-6,故知bn= -(λ+6)?(-年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image275.gif) )n-1,于是可得
)n-1,于是可得
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image282.jpg)
當(dāng)n為正奇數(shù)時(shí),1<f(n)年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image284.gif)
∴f(n)的最大值為f(1)=年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image286.gif) ,f(n)的最小值為f(2)=
,f(n)的最小值為f(2)= 年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image288.gif) ,
,
于是,由①式得年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image290.gif) a<-
a<-年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image292.gif) (λ+6)<
(λ+6)<年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image294.gif)
當(dāng)a<b年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image296.gif)
年度高三第一學(xué)期期中統(tǒng)考數(shù)學(xué)試卷(文).files/image298.gif) -
-
當(dāng)b>
且λ的取值范圍是(-b-6, -
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com