
題目列表(包括答案和解析)
| 2 |
| 1+x |
| fn(0)-1 |
| fn(0)+2 |
| Q | n |
| 4n2+n |
| 4n2+4n+1 |
(本小題滿分14分)
已知數列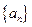 的前
的前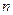 項和
項和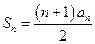 ,且
,且 .
.
(1)求數列{an}的通項公式;
(2)令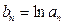 ,是否存在
,是否存在 (
( ),使得
),使得 、
、 、
、 成等比數列.若存在,求出所有符合條件的
成等比數列.若存在,求出所有符合條件的 值;若不存在,請說明理由.
值;若不存在,請說明理由.
已知數列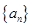 的首項
的首項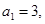 前
前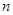 項和為
項和為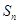 ,且
,且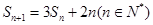 ,
,
(1)試判斷數列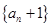 是否成等比數列?并求出數列
是否成等比數列?并求出數列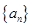 的通項公式;
的通項公式;
(2)記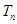 為數列
為數列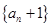 前
前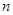 項和,求
項和,求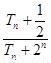 的最小值.
的最小值.
已知數列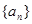 的通項公式為
的通項公式為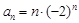 ,則數列{
,則數列{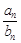 }成等比數列是數列
}成等比數列是數列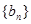 的通
的通
項公式為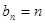 的 條件(對充分性和必要性都要作出判斷).
的 條件(對充分性和必要性都要作出判斷).
(本小題滿分12分)
已知數列![]() 的通項公式為
的通項公式為![]()
(1)若![]() 成等比數列,求
成等比數列,求![]() 的值;
的值;
(2)當![]() 且
且![]() 時,
時,![]() 成等差數列,求
成等差數列,求![]() 的值。
的值。
一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
選項
C
C
D
C
D
C
B
B
C
A
二、填空題
11. 12. 13.必要不充分 14.5 15. 16.③
三、解答題
17.解:(1)令
令
(2)
(同上,)
18.(普通班)
解:設二次函數
又
符合
(2)
18.(成志班)
解:(1) ①
②
①―②得
而
數列為首項,2為公比的比數列
(2)
(3)由于
當
當
當
又
同上:
19.解(1)(2)
(3)
用錯項相減 得
(4)
而
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com