
題目列表(包括答案和解析)
 是定義在實(shí)數(shù)有R上的奇函數(shù),若x≥0時(shí),
是定義在實(shí)數(shù)有R上的奇函數(shù),若x≥0時(shí),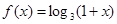 ,則
,則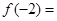 ___
__.
___
__.
 是定義在實(shí)數(shù)有R上的奇函數(shù),若x≥0時(shí),
是定義在實(shí)數(shù)有R上的奇函數(shù),若x≥0時(shí),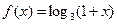 ,則
,則 ___ __.
___ __.
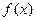 是定義在實(shí)數(shù)有R上的奇函數(shù),若x≥0時(shí),
是定義在實(shí)數(shù)有R上的奇函數(shù),若x≥0時(shí),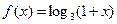 ,則
,則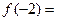 ___ __.
___ __.1.A 2.B 3.D 4.C 5.B 6.D 7.C 8.A 9.B 10.C(文、理)
11.B(文理) 12.C 13.-1 14.-2 15.①③④
16.①③④
17.設(shè)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image233.gif) :該工人在第一季度完成任務(wù)的月數(shù),
:該工人在第一季度完成任務(wù)的月數(shù),學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image235.gif) :該工人在第一季度所得獎(jiǎng)金數(shù),則
:該工人在第一季度所得獎(jiǎng)金數(shù),則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image233.gif) 與
與學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image235.gif) 的分布列如下:
的分布列如下:
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image237.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image239.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image241.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image243.gif)
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image245.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image247.gif) .
.
答:該工人在第一季度里所得獎(jiǎng)金的期望為153.75元.
18.(1)∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image249.gif) ∴
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image251.gif) ,且p=1,或
,且p=1,或學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image253.gif) .
.
若是學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image251.gif) ,且p=1,則由
,且p=1,則由學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image256.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image258.gif) ,矛盾.故不可能是:
,矛盾.故不可能是:學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image251.gif) ,且p=1.由
,且p=1.由學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image253.gif) ,得
,得學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image262.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image256.gif) ,∴
,∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image265.gif) .
.
(2)∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image267.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image269.gif) ,
,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image271.gif) .
.
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image273.gif) .
.
當(dāng)k≥2時(shí),學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image275.gif) . ∴ n≥3時(shí)有
. ∴ n≥3時(shí)有
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image277.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image279.gif) .
.
∴ 對(duì)一切學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image281.gif) 有:
有:學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image283.gif) .
.
(3)∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image285.gif) ,
,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image287.gif) .
. 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image289.gif) .
.
故學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image291.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image293.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image295.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image297.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image299.gif) .
.
故 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image177.gif) .
.
19.(甲)(1)∵ 側(cè)面學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image302.gif) 底面ABC, ∴
底面ABC, ∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image190.gif) 在平面ABC上的射影是AC.
在平面ABC上的射影是AC.
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image190.gif) 與底面ABC所成的角為∠
與底面ABC所成的角為∠學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image304.gif) .
.
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image306.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image308.gif) , ∴ ∠
, ∴ ∠學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image304.gif) =45°.
=45°.
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image310.jpg)
(2)作學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image312.gif) ⊥AC于O,則
⊥AC于O,則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image312.gif) ⊥平面ABC,再作OE⊥AB于E,連結(jié)
⊥平面ABC,再作OE⊥AB于E,連結(jié)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image314.gif) ,則
,則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image316.gif) ,所以∠
,所以∠學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image318.gif) 就是側(cè)面
就是側(cè)面學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image192.gif) 與底面ABC所成二面角的平面角.
與底面ABC所成二面角的平面角.
在Rt△學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image318.gif) 中,
中,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image321.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image323.gif) ,
,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image325.gif) .
. 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image327.gif) 60°.
60°.
(3)設(shè)點(diǎn)C到側(cè)面學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image192.gif) 的距離為x.
的距離為x.
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image329.gif) ,
,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image331.gif) .(*)
.(*)
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image333.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image335.gif) , ∴
, ∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image337.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image339.gif) ,∴
,∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image341.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image343.gif) . ∴ 由(*)式,得
. ∴ 由(*)式,得學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image345.gif) .∴
.∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image347.gif)
(乙)(1)證明:如圖,以O為原點(diǎn)建立空間直角坐標(biāo)系.
設(shè)AE=BF=x,則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image349.gif) (a,0,a),F(a-x,a,0),
(a,0,a),F(a-x,a,0),學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image008.gif) (0,a,a),E(a,x,0),
(0,a,a),E(a,x,0),
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image352.gif) (-x,a,-a),
(-x,a,-a),
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image354.gif) (a,x-a,-a).
(a,x-a,-a).
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image356.gif) ,
,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image196.gif) .
.
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image359.jpg)
(2)解:記BF=x,BE=y,則x+y=a,則三棱錐學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image198.gif) 的體積為
的體積為
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image362.gif) .
.
當(dāng)且僅當(dāng)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image364.gif) 時(shí),等號(hào)成立,因此,三棱錐
時(shí),等號(hào)成立,因此,三棱錐學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image198.gif) 的體積取得最大值時(shí),
的體積取得最大值時(shí),學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image367.gif) .
.
過(guò)B作BD⊥BF交EF于D,連結(jié)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image369.gif) ,則
,則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image371.gif) .
.
∴ ∠學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image373.gif) 是二面角
是二面角學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image200.gif) 的平面角.在Rt△BEF中,直角邊
的平面角.在Rt△BEF中,直角邊學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image376.gif) ,BD是斜邊上的高, ∴
,BD是斜邊上的高, ∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image378.gif)
在Rt△學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image373.gif) 中,tan∠
中,tan∠學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image381.gif) .故二面角
.故二面角學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image383.gif) 的大小為
的大小為學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image385.gif) .
.
20.∵ k=0不符合題意, ∴ k≠0,作直線學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image387.gif) :
:
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image389.gif) ,則
,則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image391.gif) .
.
∴ 滿足條件的
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image393.gif)
由學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image395.gif) 消去x,得
消去x,得
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image397.gif) ,
,
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image399.gif) .
.學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image401.gif) .(*)
.(*)
設(shè)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image403.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image405.gif) 、
、學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image407.gif) 、
、學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image405.gif) ,則
,則 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image410.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image412.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image414.gif) .
.
故AB的中點(diǎn)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image416.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image418.gif) . ∵ l過(guò)E, ∴
. ∵ l過(guò)E, ∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image420.gif) ,即
,即 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image422.gif) .
.
代入(*)式,得
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image424.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image426.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image428.gif)
21.(1)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image430.gif) .當(dāng)x≥2時(shí),
.當(dāng)x≥2時(shí),
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image432.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image434.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image436.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image438.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image440.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image442.gif) ,且
,且學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image206.gif) .
.
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image445.gif) .
.
∴ 當(dāng)x=12-x,即x=6時(shí),學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image447.gif) (萬(wàn)件).故6月份該商品的需求量最大,最大需求量為
(萬(wàn)件).故6月份該商品的需求量最大,最大需求量為學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image449.gif) 萬(wàn)件.
萬(wàn)件.
(2)依題意,對(duì)一切學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image451.gif) {1,2,…,12}有
{1,2,…,12}有學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image453.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image455.gif) (x=1,2,…,12).
(x=1,2,…,12).
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image457.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image459.gif)
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image461.gif) . 故 p≥1.14.故每個(gè)月至少投放1.14萬(wàn)件,可以保證每個(gè)月都保證供應(yīng).
. 故 p≥1.14.故每個(gè)月至少投放1.14萬(wàn)件,可以保證每個(gè)月都保證供應(yīng).
22.(1)按題意,得學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image463.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image465.gif) 即
即 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image467.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image469.gif)
∴ 關(guān)于x的方程學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image471.gif) .
.
在(2,+∞)內(nèi)有二不等實(shí)根x=學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image212.gif) 、
、學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image214.gif) .
.學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image475.gif) 關(guān)于x的二次方程
關(guān)于x的二次方程學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image477.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image479.gif) 在(2,+∞)內(nèi)有二異根
在(2,+∞)內(nèi)有二異根學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image212.gif) 、
、學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image214.gif) .
.
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image483.gif) .
.
故 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image485.gif) .
.
(2)令學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image487.gif) ,則
,則學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image489.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image491.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image493.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image224.gif) .
.
(3)∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image496.gif) ,
,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image498.gif)
學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image500.gif) .
.
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image502.gif) , ∴ 當(dāng)
, ∴ 當(dāng)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image451.gif) (
(學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image212.gif) ,4)時(shí),
,4)時(shí),學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image506.gif) ;當(dāng)
;當(dāng)學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image451.gif) (4,
(4,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image214.gif) )是
)是學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image506.gif) .
.
又學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image208.gif) 在[
在[學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image212.gif) ,
,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image214.gif) ]上連接,
]上連接,
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image208.gif) 在[
在[學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image212.gif) ,4]上遞增,在[4,
,4]上遞增,在[4,學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image214.gif) ]上遞減.
]上遞減.
故 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image514.gif) .
.
∵ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image485.gif) ,
,
∴ 0<學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image517.gif) .
.
∴ 學(xué)模擬題精編詳解第八套-人教新課標(biāo).files/image519.gif) ,矛盾.故0<M<1.
,矛盾.故0<M<1.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com