
題目列表(包括答案和解析)
(本小題滿分14分)
本題是選作題,考生只能選做其中兩個小題.三個小題都作答的,以前兩個小題計算得分。
①選修4-4《坐標系與參數方程》選做題(本小題滿分7分)
已知曲線C的參數方程是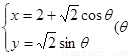 為參數),且曲線C與直線
為參數),且曲線C與直線 =0相交于兩點A、B求弦AB的長。
=0相交于兩點A、B求弦AB的長。
②選修4-2《矩陣與變換》選做題(本小題滿分7分)
已知矩陣 的一個特征值為
的一個特征值為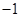 ,它對應的一個特征向量
,它對應的一個特征向量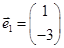 。
。
(Ⅰ)求矩陣M;
(Ⅱ)點P(1, 1)經過矩陣M所對應的變換,得到點Q,求點Q的坐標。
③選修4-5《不等式選講》選做題(本小題滿分7分)
函數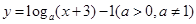 的圖象恒過定點
的圖象恒過定點 ,若點
,若點 在直
在直 線
線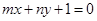 上,其中
上,其中
 ,求
,求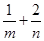 的最小值。
的最小值。

(本小題滿分14分)
本題是選作題,考生只能選做其中兩個小題.三個小題都作答的,以前兩個小題計算得分。
①選修4-4《坐標系與參數方程》選做題(本小題滿分7分)
已知曲線C的參數方程是 為參數),且曲線C與直線
為參數),且曲線C與直線 =0相交于兩點A、B求弦AB的長。
=0相交于兩點A、B求弦AB的長。
②選修4-2《矩陣與變換》選做題(本小題滿分7分)
已知矩陣 的一個特征值為
的一個特征值為 ,它對應的一個特征向量
,它對應的一個特征向量 。
。
(Ⅰ)求矩陣M;
(Ⅱ)點P(1, 1)經過矩陣M所對應的變換,得到點Q,求點Q的坐標。
③選修4-5《不等式選講》選做題(本小題滿分7分)
函數 的圖象恒過定點
的圖象恒過定點 ,若點
,若點 在直
在直 線
線 上,其中
上,其中 ,求
,求 的最小值。
的最小值。
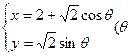 為參數),且曲線C與直線
為參數),且曲線C與直線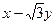 =0相交于兩點A、B求弦AB的長。
=0相交于兩點A、B求弦AB的長。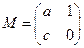 的一個特征值為
的一個特征值為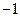 ,它對應的一個特征向量
,它對應的一個特征向量 。
。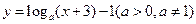 的圖象恒過定點
的圖象恒過定點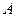 ,若點
,若點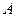 在直
在直 線
線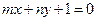 上,其中
上,其中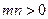 ,求
,求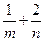 的最小值。
的最小值。已知實數m>1,定點A(-m,0),B(m,0),S為一動點,點S與A,B兩點連線斜率之積為![]()
(1)求動點S的軌跡C的方程,并指出它是哪一種曲線;
(2)當![]() 時,問t取何值時,直線
時,問t取何值時,直線![]() 與曲線C有且只有一個交點?
與曲線C有且只有一個交點?
(3)在(2)的條件下,證明:直線l上橫坐標小于2的點P到點(1,0)的距離與到直線x=2的距離之比的最小值等于曲線C的離心率.
已知實數m>1,定點A(-m,0),B(m,0),S為一動點,點S與A,B兩點連線斜率之積為![]()
(1)求動點S的軌跡C的方程,并指出它是哪一種曲線;
(2)當![]() 時,問t取何值時,直線
時,問t取何值時,直線![]() 與曲線C有且只有一個交點?
與曲線C有且只有一個交點?
(3)在(2)的條件下,證明:直線l上橫坐標小于2的點P到點(1,0)的距離與到直線x=2的距離之比的最小值等于曲線C的離心率.
二、選擇題
題號
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
C
B
C
A
三、填空題
(11){x│x<1 } (12)  (13) 3 (14)m=0或m≥1 (15) 2004
(13) 3 (14)m=0或m≥1 (15) 2004
(16)②③④
三解答題
(17)(Ⅰ) ; (Ⅱ)
; (Ⅱ) .
.
(18)解:由題目知 的圖像是開口向下,交
的圖像是開口向下,交 軸于兩點
軸于兩點 和
和 的拋物線,對稱軸方程為
的拋物線,對稱軸方程為 (如圖)
(如圖)
那么,當 和
和 時,有
時,有 ,代入原式得:
,代入原式得:

解得: 或
或 
經檢驗知: 不符合題意,舍去.
不符合題意,舍去.

(Ⅰ)由圖像知,函數在 內為單調遞減,所以:當
內為單調遞減,所以:當 時,
時, ,當
,當 時,
時, .
.
 在
在 內的值域為
內的值域為
(Ⅱ)令
要使 的解集為R,則需要方程
的解集為R,則需要方程 的根的判別式
的根的判別式 ,即
,即
解得 
 當
當 時,
時, 的解集為R.
的解集為R.
(19)(Ⅰ) ; (Ⅱ)存在M=4.
; (Ⅱ)存在M=4.
(20)解:任設x 1>x2
f(x 1)-f(x2) = a x 1+ - a x 2 -
- a x 2 -
=(x 1-x 2)(a+  )
)
∵f(x)是R上的減函數,
∴(x 1-x
2)(a+  )<0恒成立
)<0恒成立
又 <1
<1
∴a≤ -1
(21)解:(Ⅰ)由已知


 ,
,
(Ⅱ)設 ,
,

當且僅當 時,
時,

(Ⅲ)




 橢圓的方程為
橢圓的方程為
(22)(Ⅰ) .
.
(Ⅱ) 的單調遞增區間為
的單調遞增區間為 ,單調遞減區間為
,單調遞減區間為 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com