題目列表(包括答案和解析)
甲、乙、丙三人按下面的規則進行乒乓球比賽：第一局由甲、乙參加而丙輪空，以后每一局由前一局的獲勝者與輪空者進行比賽，而前一局的失敗者輪空.比賽按這種規則一直進行到其中一人連勝兩局或打滿6局時停止.設在每局中參賽者勝負的概率均為
，且各局勝負相互獨立.求：
（Ⅰ）打滿3局比賽還未停止的概率；
（Ⅱ）比賽停止時已打局數
的分別列與期望E.
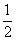，且各局勝負相互獨立。
，且各局勝負相互獨立．求：
，且各局勝負相互獨立．求：
，且各局勝負相互獨立．求：1-8 BACBD BDD
9.
10. 400 11. 
12. 128 13.. 
14.
15.
解析：5．數形結合法 7．解:由圖知三角形ABC為等腰三角形,只要∠AF2B為銳角即可,所以有
,即
,解出
,故選D
8．由已知得
圖關于
軸對稱，且的周期是2，所以可作出在[-1，1]的圖象，由圖的單增性結合三角函數值可判斷D。
12.解:當
時,
,相減得
,且由已知得
,所以所求為
14，因為
由題意得
，解得
15，解:由題知△BED～△BCE,所以
，可求得BE=
16．解：(Ⅰ)由題意得
由A為銳角得
，
(Ⅱ)由(Ⅰ)知
,所以
因為
,所以
,因此，當
時,
有最大值
,
當
時,有最小值
? 3，所以所求函數的值域是
17.解：令
分別表示甲、乙、丙在第k局中獲勝.
（Ⅰ）由獨立事件同時發生與互斥事件至少有一個發生的概率公式知，打滿3局比賽還未停止的概率為
（Ⅱ）
的所有可能值為2，3，4，5，6，且
故有分布列
2
3
4
5
6
P
從而
（局）.
18．證（1）因為
側面
，故
在
中，
由余弦定理有
故有 
而
且
平面
（2）
從而
且
故
不妨設 
，則
，則
又
則
在
中有
從而
（舍負）
故
為
的中點時，
（3）取
的中點
，
的中點
，
的中點
，
的中點
連
則
，連
則
，連
則
連
則
，且
為矩形，
又
故
為所求二面角的平面角
在
中，
19．解：（1）依題意，
到
距離等于到直線
的距離，曲線
是以原點為頂點，為焦點的拋物線 
曲線方程是
（2）設圓心
，因為圓過
故設圓的方程
令
得：
設圓與軸的兩交點為
，則
在拋物線上，
所以，當運動時，弦長
為定值2
20．解：（1）
，依題意有
，故
．
從而
．
的定義域為
，當
時，
；
當
時，
；當
時，．
從而，分別在區間
單調增加，在區間
單調減少．
（2）的定義域為
，
．
方程
的判別式
．
①若
，即
，在的定義域內，故無極值．
②若
，則
或
．若，
，
．
當
時，
，當
時，，所以無極值．若，
，
，也無極值．
③若
，即
或
，則有兩個不同的實根
，
．
當時，
，從而
有的定義域內沒有零點，故無極值．
當時，
，
，在的定義域內有兩個不同的零點，由根值判別方法知在
取得極值．綜上，存在極值時，
的取值范圍為
．的極值之和為
．
21．解：（1）由點P
在直線
上，即
，且
，數列{
}
是以1為首項，1為公差的等差數列
，同樣滿足，所以
（2）
所以
是單調遞增，故的最小值是
（3）
，可得
，
，
……
，n≥2
故存在關于n的整式g（x）=n,使得對于一切不小于2的自然數n恒成立.
（2）法二：以
為原點
為
軸，設，則
由得 
即
化簡整理得
，
或 
當時與
重合不滿足題意
當時為的中點
故為的中點使
（3）法二：由已知
，
所以二面角
的平面角
的大小為向量
與
的夾角 因為
同步練習冊答案
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com