
題目列表(包括答案和解析)
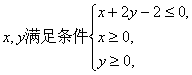 則該不等式組表示的平面圖形的面積是 ;代數式
則該不等式組表示的平面圖形的面積是 ;代數式把函數 的圖象按向量
的圖象按向量 平移得到函數
平移得到函數 的圖象.
的圖象.
(1)求函數 的解析式; (2)若
的解析式; (2)若 ,證明:
,證明: .
.
【解析】本試題主要考查了函數 平抑變換和運用函數思想證明不等式。第一問中,利用設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 ,便可以得到結論。第二問中,令
,便可以得到結論。第二問中,令 ,然后求導,利用最小值大于零得到。
,然后求導,利用最小值大于零得到。
(1)解:設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 證明:令 ,……6分
,……6分
則 ……8分
……8分
 ,∴
,∴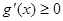 ,∴
,∴ 在
在 上單調遞增.……10分
上單調遞增.……10分
故 ,即
,即
已知函數 的圖象過坐標原點O,且在點
的圖象過坐標原點O,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實數 的值;
的值;
(Ⅱ)求 在區間
在區間 上的最大值;
上的最大值;
(Ⅲ)對任意給定的正實數 ,曲線
,曲線 上是否存在兩點P、Q,使得
上是否存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上?說明理由.
軸上?說明理由.
【解析】第一問當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問當 時,
時, ,令
,令 得
得 ,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
第三問假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
(Ⅰ)當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當 時,
時, ,令
,令 得
得
當 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當 時,
時,  .當
.當 時,
時,  ,
, 最大值為0;
最大值為0;
當 時,
時,  在
在 上單調遞增。∴
上單調遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為2;
上的最大值為2;
當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無解,因此
,而此方程無解,因此 。此時
。此時 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調遞增, ∵
上單調遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對任意給定的正實數 ,曲線
,曲線 上存在兩點P、Q,使得
上存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上
軸上
一、選擇題:本大題共有8個小題,每小題5分,共40分;在每個小題給出的四個選項中有且僅有一個是符合題目要求的。
1―8 BDABADBC
二、填空題:本大題共有6個小題,每小題5分,共30分;請把答案寫在相應的位置上。
9.5 10. 11.7 12.
11.7 12. 13.
13. 14.
14.
三、解答題:本大題共6個小題,共80分;解答應寫出文字說明,證明過程或演算步驟。
15.(本題滿分13分)
解:(1)

(2)

16.(本題滿分13分)
解: 用A,B,C分別表示事件甲、乙、丙面試合格.
由題意知A,B,C相互獨立,且
P(A)=P(B)=P(C)= .
.
(Ⅰ)至少有1人面試合格的概率是
 …………………6分
…………………6分
(2)沒有人簽約的概率為

 ………………13分
………………13分
17.(本題滿分13分)
解法1:(1)連結A1B,則D1E在側面ABB
又∵A1B⊥AB1,