
題目列表(包括答案和解析)
已知中心在坐標(biāo)原點(diǎn),焦點(diǎn)在 軸上的橢圓C;其長(zhǎng)軸長(zhǎng)等于4,離心率為
軸上的橢圓C;其長(zhǎng)軸長(zhǎng)等于4,離心率為 .
.
(Ⅰ)求橢圓C的標(biāo)準(zhǔn)方程;
(Ⅱ)若點(diǎn) (0,1), 問(wèn)是否存在直線
(0,1), 問(wèn)是否存在直線 與橢圓
與橢圓 交于
交于 兩點(diǎn),且
兩點(diǎn),且 ?若存在,求出
?若存在,求出 的取值范圍,若不存在,請(qǐng)說(shuō)明理由.
的取值范圍,若不存在,請(qǐng)說(shuō)明理由.
【解析】本試題主要考查了橢圓的方程的求解,直線與橢圓的位置關(guān)系的運(yùn)用。
第一問(wèn)中,可設(shè)橢圓的標(biāo)準(zhǔn)方程為
則由長(zhǎng)軸長(zhǎng)等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求橢圓C的標(biāo)準(zhǔn)方程為
第二問(wèn)中,
假設(shè)存在這樣的直線 ,設(shè)
,設(shè) ,MN的中點(diǎn)為
,MN的中點(diǎn)為
因?yàn)閨ME|=|NE|所以MN EF所以
EF所以
(i)其中若 時(shí),則K=0,顯然直線
時(shí),則K=0,顯然直線 符合題意;
符合題意;
(ii)下面僅考慮 情形:
情形:
由 ,得,
,得,
 ,得
,得
代入1,2式中得到范圍。
(Ⅰ) 可設(shè)橢圓的標(biāo)準(zhǔn)方程為
則由長(zhǎng)軸長(zhǎng)等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求橢圓C的標(biāo)準(zhǔn)方程為
(Ⅱ) 假設(shè)存在這樣的直線 ,設(shè)
,設(shè) ,MN的中點(diǎn)為
,MN的中點(diǎn)為
因?yàn)閨ME|=|NE|所以MN EF所以
EF所以
(i)其中若 時(shí),則K=0,顯然直線
時(shí),則K=0,顯然直線 符合題意;
符合題意;
(ii)下面僅考慮 情形:
情形:
由 ,得,
,得,
 ,得
,得 ……② ……………………9分
……② ……………………9分
則 .
.
代入①式得,解得 ………………………………………12分
………………………………………12分
代入②式得 ,得
,得 .
.
綜上(i)(ii)可知,存在這樣的直線 ,其斜率k的取值范圍是
,其斜率k的取值范圍是
 的直線l,交雙曲線左支于A,B兩點(diǎn),交y軸于點(diǎn)C,且滿足|PA|· |PB|=|PC|2。
的直線l,交雙曲線左支于A,B兩點(diǎn),交y軸于點(diǎn)C,且滿足|PA|· |PB|=|PC|2。 上一動(dòng)點(diǎn),求|MN|的取值范圍。
上一動(dòng)點(diǎn),求|MN|的取值范圍。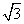 sinθ+cosθ,其中,角θ的頂點(diǎn)與坐標(biāo)原點(diǎn)重合,始邊與x軸非負(fù)半軸重合,終邊經(jīng)過(guò)點(diǎn)P(x,y),且0≤θ≤π。
sinθ+cosθ,其中,角θ的頂點(diǎn)與坐標(biāo)原點(diǎn)重合,始邊與x軸非負(fù)半軸重合,終邊經(jīng)過(guò)點(diǎn)P(x,y),且0≤θ≤π。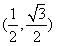 ,求f(θ)的值。
,求f(θ)的值。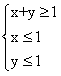 上的一個(gè)動(dòng)點(diǎn),試確定角θ的取值范圍,并求函數(shù)f(θ)的最小值和最大值。
上的一個(gè)動(dòng)點(diǎn),試確定角θ的取值范圍,并求函數(shù)f(θ)的最小值和最大值。.橢圓
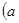 >
> >
>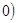 與直線
與直線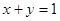 交于
交于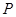 、
、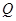 兩點(diǎn),且
兩點(diǎn),且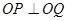 ,其
,其
中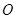 為坐標(biāo)原點(diǎn)。
為坐標(biāo)原點(diǎn)。
1)求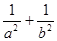 的值;
的值;
2)若橢圓的離心率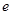 滿足
滿足 ,求橢圓長(zhǎng)軸的取值范圍。
,求橢圓長(zhǎng)軸的取值范圍。
1.解析: ,故選A。
,故選A。
2.解析:∵
 ,
,
故選B。
3.解析:由 ,得
,得 ,此時(shí)
,此時(shí) ,所以,
,所以, ,故選C。
,故選C。
4.解析:顯然,若 與
與 共線,則
共線,則 與
與 共線;若
共線;若 與
與 共線,則
共線,則 ,即
,即
 ,得
,得 ,∴
,∴ 與
與 共線,∴
共線,∴ 與
與 共線是
共線是 與
與 共線的充要條件,故選C。
共線的充要條件,故選C。
5.解析:設(shè)公差為 ,由題意得,
,由題意得, ;
; ,解得
,解得 或
或 ,故選C。
,故選C。
6.解析:∵雙曲線 的右焦點(diǎn)到一條漸近線的距離等于焦距的
的右焦點(diǎn)到一條漸近線的距離等于焦距的 ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ ,∴雙曲線的離心率是
,∴雙曲線的離心率是 。故選B.
。故選B.
7.解析:∵ 、
、 為正實(shí)數(shù),∴
為正實(shí)數(shù),∴ ,∴
,∴ ;由均值不等式得
;由均值不等式得 恒成立,
恒成立, ,故②不恒成立,又因?yàn)楹瘮?shù)
,故②不恒成立,又因?yàn)楹瘮?shù) 在
在 是增函數(shù),∴
是增函數(shù),∴ ,故恒成立的不等式是①③④。故選C.
,故恒成立的不等式是①③④。故選C.
8.解析:∵ ,∴
,∴ 在區(qū)間
在區(qū)間 上恒成立,即
上恒成立,即 在區(qū)間
在區(qū)間 上恒成立,∴
上恒成立,∴ ,故選D。
,故選D。
9.解析:∵

 ,此函數(shù)的最小值為
,此函數(shù)的最小值為 ,故選C。
,故選C。
10.解析:如圖,∵正三角形 的邊長(zhǎng)為
的邊長(zhǎng)為 ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,故選D。
,故選D。
11.解析:∵ 在區(qū)間
在區(qū)間 上是增函數(shù)且
上是增函數(shù)且 ,∴其反函數(shù)
,∴其反函數(shù) 在區(qū)間上
在區(qū)間上 是增函數(shù),∴
是增函數(shù),∴

 ,故選A
,故選A
12.解析:如圖,①當(dāng) 或
或 時(shí),圓面
時(shí),圓面 被分成2塊,涂色方法有20種;②當(dāng)
被分成2塊,涂色方法有20種;②當(dāng) 或
或 時(shí),圓面
時(shí),圓面 被分成3塊,涂色方法有60種;
被分成3塊,涂色方法有60種;
③當(dāng) 時(shí),圓面
時(shí),圓面 被分成4塊,涂色方法有120種,所以m的取值范圍是
被分成4塊,涂色方法有120種,所以m的取值范圍是 ,故選A。
,故選A。
13.解析:做出 表示的平面區(qū)域如圖,當(dāng)直線
表示的平面區(qū)域如圖,當(dāng)直線 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn) 時(shí),
時(shí), 取得最大值5。
取得最大值5。
 14.解析:∵
14.解析:∵ ,∴
,∴ 時(shí),
時(shí), ,又
,又 時(shí),
時(shí), 滿足上式,因此,
滿足上式,因此, ,
,
∴ 。
。
 15.解析:設(shè)正四面體的棱長(zhǎng)為
15.解析:設(shè)正四面體的棱長(zhǎng)為 ,連
,連 ,取
,取 的中點(diǎn)
的中點(diǎn) ,連
,連 ,∵
,∵ 為
為 的中點(diǎn),∴
的中點(diǎn),∴ ∥
∥ ,∴
,∴ 或其補(bǔ)角為
或其補(bǔ)角為 與
與 所成角,∵
所成角,∵ ,
, ,∴
,∴ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ 與
與 所成角的余弦值為
所成角的余弦值為 。
。
 16.解析:∵
16.解析:∵ ,∴
,∴ ,∵點(diǎn)
,∵點(diǎn) 為
為 的準(zhǔn)線與
的準(zhǔn)線與 軸的交點(diǎn),由向量的加法法則及拋物線的對(duì)稱性可知,點(diǎn)
軸的交點(diǎn),由向量的加法法則及拋物線的對(duì)稱性可知,點(diǎn) 為拋物線上關(guān)于軸對(duì)稱的兩點(diǎn)且做出圖形如右圖,其中
為拋物線上關(guān)于軸對(duì)稱的兩點(diǎn)且做出圖形如右圖,其中 為點(diǎn)
為點(diǎn) 到準(zhǔn)線的距離,四邊形
到準(zhǔn)線的距離,四邊形 為菱形,∴
為菱形,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,∴向量
,∴向量 與
與 的夾角為
的夾角為 。
。
17.(10分)解析:(Ⅰ)由正弦定理得, ,
, ,…2分
,…2分
∴ ,
, ,………4分
,………4分
(Ⅱ)∵ ,
, ,∴
,∴ ,∴
,∴ ,………………………6分
,………………………6分
又∵ ,∴
,∴ ,∴
,∴ ,………………………8分
,………………………8分
∴ 。………………………10分
。………………………10分
18.解析:(Ⅰ)∵ ,∴
,∴ ;……………………理3文4分
;……………………理3文4分
(Ⅱ)∵三科會(huì)考不合格的概率均為 ,∴學(xué)生甲不能拿到高中畢業(yè)證的概率
,∴學(xué)生甲不能拿到高中畢業(yè)證的概率 ;……………………理6文8分
;……………………理6文8分
(Ⅲ)∵每科得A,B的概率分別為 ,∴學(xué)生甲被評(píng)為三好學(xué)生的概率為
,∴學(xué)生甲被評(píng)為三好學(xué)生的概率為 。……………………12分
。……………………12分
(理)∵
 ,
, ,
, ,
, 。……………………9分
。……………………9分
∴ 的分布列如下表:
的分布列如下表:

0
1
2
3





∴ 的數(shù)學(xué)期望
的數(shù)學(xué)期望
 。……………………12分
。……………………12分
19.(12分)解析:(Ⅰ) 時(shí),
時(shí),
 ,
,
 ,
,


由 得,
得, 或
或 ………3分
………3分







+
0
-
0
+

遞增
極大值
遞減
極小值
遞增
 ,
, ………………………6分
………………………6分
(Ⅱ) 在定義域
在定義域 上是增函數(shù),
上是增函數(shù),

 對(duì)
對(duì) 恒成立,即
恒成立,即
 ………………………9分
………………………9分
又 (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) 時(shí),
時(shí), )
)

 ………………………4分
………………………4分

20.解析:(Ⅰ)∵ ∥
∥ ,
, ,∴
,∴ ,∵
,∵ 底面
底面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ ,又∵
,又∵ 平面
平面 ,∴
,∴ ,∴
,∴ 平面
平面 ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)∵ 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 為二面角
為二面角 的平面角,………………………6分
的平面角,………………………6分
 ,
, ,∴
,∴ ,又∵
,又∵ 平面
平面 ,
, ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小為
的正切值的大小為 。………………………8分
。………………………8分
(Ⅲ)過(guò)點(diǎn) 做
做 ∥
∥ ,交
,交 于點(diǎn)
于點(diǎn) ,∵
,∵ 平面
平面 ,∴
,∴ 為
為 在平面
在平面 內(nèi)的射影,∴
內(nèi)的射影,∴ 為
為 與平面
與平面 所成的角,………………………10分
所成的角,………………………10分
 ∵
∵ ,∴
,∴ ,又∵
,又∵ ∥
∥ ,∴
,∴ 和
和 與平面
與平面 所成的角相等,∴
所成的角相等,∴ 與平面
與平面 所成角的正切值為
所成角的正切值為 。………………………12分
。………………………12分
解法2:如圖建立空間直角坐標(biāo)系,(Ⅰ)∵, ,∴點(diǎn)
,∴點(diǎn) 的坐標(biāo)分別是
的坐標(biāo)分別是 ,
, ,
,
 ,∴
,∴ ,
, ,設(shè)
,設(shè) ,∵
,∵ 平面
平面 ,∴
,∴ ,∴
,∴ ,取
,取 ,∴
,∴ ,∴
,∴ 。………………………4分
。………………………4分
(Ⅱ)設(shè)二面角 的大小為
的大小為 ,∵平面
,∵平面 的法向量是
的法向量是 ,平面
,平面 的法向量是
的法向量是 ,∴
,∴ ,∴
,∴ ,∴二面角
,∴二面角 的正切值的大小為
的正切值的大小為 。………………………8分
。………………………8分
(Ⅲ)設(shè) 與平面
與平面 所成角的大小為
所成角的大小為 ,∵平面
,∵平面 的法向量是
的法向量是 ,
, ,∴
,∴ ,∴
,∴ ,∴
,∴ 與平面
與平面 所成角的正切值為
所成角的正切值為 。………………………12分
。………………………12分
21.(Ⅰ) 解析:如圖,設(shè)右準(zhǔn)線 與
與 軸的交點(diǎn)為
軸的交點(diǎn)為 ,過(guò)點(diǎn)
,過(guò)點(diǎn) 分別向
分別向 軸及右準(zhǔn)線引垂線
軸及右準(zhǔn)線引垂線 ,∵
,∵ ,∴
,∴ ,又∵
,又∵ ∥
∥ ,∴
,∴
 ,………………………2分
,………………………2分
∴ ,又∵
,又∵ ,∴
,∴ ,又∵
,又∵ ,解得
,解得 ,∴
,∴ ,∴雙曲線
,∴雙曲線 的方程為
的方程為 。………………………4分
。………………………4分
(Ⅱ)聯(lián)立方程組  消
消 得:
得:
由直線 與雙曲線
與雙曲線 交于不同的兩點(diǎn)得:
交于不同的兩點(diǎn)得:
即  于是
于是  ,且
,且 ………………①………………………6分
………………①………………………6分
設(shè) 、
、 ,則
,則

 ……………………9分
……………………9分
又 ,所以
,所以 ,解得
,解得
 ……………②
……………②
由①和②得
 即
即 或
或
故 的取值范圍為
的取值范圍為 。………………………12分
。………………………12分
22.(12分)解析:(Ⅰ)∵ ,∴
,∴ ,∴
,∴ ,∴數(shù)列
,∴數(shù)列 是等差數(shù)列,………………………2分
是等差數(shù)列,………………………2分
又∵ ,
, ,∴公差為2,
,∴公差為2,
∴ ,………………………4分
,………………………4分
(Ⅱ)∵ ,∴
,∴ ,
,
∴數(shù)列 是公比為2的等比數(shù)列,
是公比為2的等比數(shù)列,
∵ ,∴
,∴ ,………………………6分
,………………………6分
(Ⅲ)∵ ,
,
∴ ………………………8分
………………………8分
∴ ………………………10分
………………………10分
 ∵
∵ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ………………………12分
………………………12分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com