
題目列表(包括答案和解析)
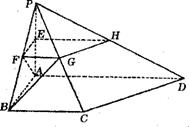
(09年萊陽一中期末理)(12分)四棱錐![]() 中,
中,
![]() ,E為PA中點,過E作平行于底面的面EFGH分別與另外三條側棱交于F, G,H已知底面ABCD為直角梯形,AD∥BC,
,E為PA中點,過E作平行于底面的面EFGH分別與另外三條側棱交于F, G,H已知底面ABCD為直角梯形,AD∥BC,![]() ,
,![]() 。
。
(1)求異面直線AF,BG所成的角的大小;
(2)設面APB與面CPD所成的銳二面角的大小為![]() ,求cos
,求cos![]() .
.
(滿分12分)設底面邊長為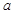 的正四棱柱
的正四棱柱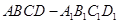 中,
中,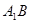 與平面
與平面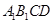 所成角為
所成角為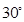 ;點
;點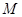 是棱
是棱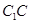 上一點.
上一點.

(1)求證:正四棱柱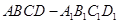 是正方體;
是正方體;
(2)若點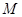 在棱
在棱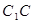 上滑動,求點
上滑動,求點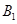 到平面
到平面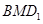 距離的最大值;
距離的最大值;
(3)在(2)的條件下,求二面角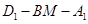 的大小.
的大小.
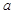 的正四棱柱
的正四棱柱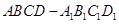 中,
中,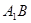 與平面
與平面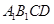 所成角為
所成角為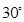 ;點
;點 是棱
是棱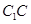 上一點.
上一點.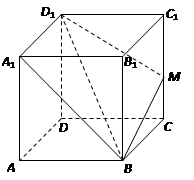
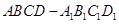 是正方體;
是正方體; 在棱
在棱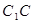 上滑動,求點
上滑動,求點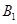 到平面
到平面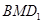 距離的最大值;
距離的最大值;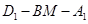 的大小.
的大小.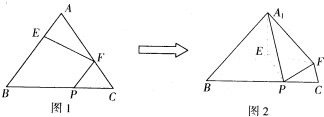 如圖1,在正三角形ABC中,已知AB=5,E、F、P分別是AB、AC、BC邊上的點,設
如圖1,在正三角形ABC中,已知AB=5,E、F、P分別是AB、AC、BC邊上的點,設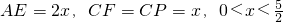 ,將△ABC沿EF折起到△A1EF的位置,使二面角A1-EF-B的大小為
,將△ABC沿EF折起到△A1EF的位置,使二面角A1-EF-B的大小為 ,連接A1B、A1P(如圖2).
,連接A1B、A1P(如圖2). ,PA=AB=2,點E為線段PB的中點,點M在弧AB上,且OM∥AC.
,PA=AB=2,點E為線段PB的中點,點M在弧AB上,且OM∥AC.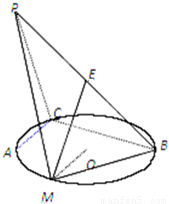
一.選擇題:本大題共12小題,每小題5分,共60分。
(1)B (2)A (3)B (4)A (5)C (6)D
(7)A (8)C (9)B (10)A (11)D (12)B
二.填空題:本大題共4小題,每小題5分,共20分。
(13) (14)
(14) (15)
(15)
(16)
三.解答題:本大題共6小題,共70分,解答應寫出文字說明,證明過程或演算步驟。
(17)(本小題滿分10分)
(Ⅰ)解法一:由正弦定理得 .
.
故  ,
,
又  ,
,
故  ,
,
即  ,
,
故  .
.
因為  ,
,
故  ,
,
又  為三角形的內角,
為三角形的內角,
所以  . ………………………5分
. ………………………5分
解法二:由余弦定理得  .
.
將上式代入 整理得
整理得 .
.
故  ,
,
又  為三角形內角,
為三角形內角,
所以  .
………………………5分
.
………………………5分
(Ⅱ)解:因為 .
.
故  ,
,
由已知  得
得

又因為  .
.
得  ,
,
所以  ,
,
解得  . ………………………………………………10分
. ………………………………………………10分
 (18)(本小題滿分12分)
(18)(本小題滿分12分)
(Ⅰ)證明:
∵ 面
面 ,
, 面
面 ,
,
∴ .
.
又∵底面 是正方形,
是正方形,
∴ .
.
又∵ ,
,
∴ 面
面 ,
,
又∵ 面
面 ,
,
∴平面
 平面
平面 . ………………………………………6分
. ………………………………………6分
(Ⅱ)解法一:如圖建立空間直角坐標系 .
.
設 ,則
,則 ,在
,在 中,
中, .
.
∴ 、
、 、
、 、
、 、
、 、
、 .
.
 ∵
∵ 為
為 的中點,
的中點, ,
,
∴ .
.
設 是平面
是平面 的一個法向量.
的一個法向量.
 則由
則由 可求得
可求得 .
.
由(Ⅰ)知 是平面
是平面 的一個法向量,
的一個法向量,
且 ,
,
∴ ,即
,即 .
.
∴二面角 的大小為
的大小為 . ………………………………………12分
. ………………………………………12分
解法二:
 設
設 ,則
,則 ,
,
在 中,
中, .
.
設 ,連接
,連接 ,過
,過 作
作 于
于 ,
,
連結 ,由(Ⅰ)知
,由(Ⅰ)知 面
面 .
.
∴ 在面
在面 上的射影為
上的射影為 ,
,
∴ .
.
故 為二面角
為二面角 的平面角.
的平面角.
在 中,
中, ,
, ,
, .
.
∴ ,
,
∴ .
.
∴ .
.
即二面角 的大小為
的大小為 . …………………………………12分
. …………………………………12分
(19)(本小題滿分12分)
(Ⅰ)解:設 、
、 兩項技術指標達標的概率分別為
兩項技術指標達標的概率分別為 、
、 .
.
由題意得: …………2分
…………2分
∴ .
.
即一個零件經過檢測為合格品的概率為 . …………6分
. …………6分
(Ⅱ)設該工人一個月生產的20件新產品中合格品有 件,獲得獎金
件,獲得獎金 元,則
元,則
 . ………………8分
. ………………8分
 ~
~ ,
, ,
………………10分
,
………………10分
 .
.
即該工人一個月獲得獎金的數學期望是800元. ………………12分
(20)(本小題滿分12分)
解:(Ⅰ)設雙曲線方程為 ,
, ,
,
由 ,
, 及勾股定理得
及勾股定理得 ,
,
由雙曲線定義得  .
.
則 .
………………………………………5分
.
………………………………………5分
(Ⅱ) ,
,
 ,故雙曲線的兩漸近線方程為
,故雙曲線的兩漸近線方程為 .
.
因為 過
過 , 且
, 且 與
與 同向,故設
同向,故設 的方程為
的方程為 ,
,
則
又 的面積
的面積 ,所以
,所以 .
.
可得 與
與 軸的交點為
軸的交點為 .
.
設 與
與 交于點
交于點 ,
, 與
與 交于點
交于點 ,
,
由 得
得 ;由
;由 得
得 .
.
故 ,
,

 ,
,
 ,
,
從而 .
.
故 的取值范圍是
的取值范圍是 . …………………………12分
. …………………………12分
(21)(本小題滿分12分)
解:(Ⅰ) ,
,
 .
.
又因為函數 在
在 上為增函數,
上為增函數,
 在
在 上恒成立,等價于
上恒成立,等價于
 在
在 上恒成立.
上恒成立.
又 ,
,
故當且僅當 時取等號,而
時取等號,而 ,
,
 的最小值為
的最小值為 .
………………………………………6分
.
………………………………………6分
(Ⅱ)由已知得:函數 為奇函數,
為奇函數,
 ,
,  , ………………………………7分
, ………………………………7分
 .
.
 切點為
切點為 ,其中
,其中 ,
,
則切線 的方程為:
的方程為: ……………………8分
……………………8分
由 ,
,
得 .
.
又 ,
,
 ,
,
 ,
,
 ,
,
 或
或 ,由題意知,
,由題意知,
從而 .
.
 ,
,
 ,
,
 .
………………………………………12分
.
………………………………………12分
(22)(本小題滿分12分)
(Ⅰ)解: 由 ,
,
 得
得
 ,
, . …………………………3分
. …………………………3分
(Ⅱ)由(Ⅰ)歸納得
 , ………………………4分
, ………………………4分
用數學歸納法證明:
①當 時,
時, 成立.
成立.
②假設 時,
時, 成立,
成立,
那么

所以當 時,等式也成立.
時,等式也成立.
由①、②得
 對一切
對一切 成立. ……………8分
成立. ……………8分
(Ⅲ)證明: 設 ,則
,則 ,
,
所以 在
在 上是增函數.
上是增函數.
故 .
.
即 .
.
因為 ,
,
故 .
.
 =
= .…………12分
.…………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com