
題目列表(包括答案和解析)
已知等比數列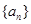 中,
中,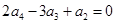 ,且
,且 ,公比
,公比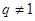 ,(1)求
,(1)求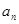 ;(2)設
;(2)設 ,求數列
,求數列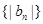 的前
的前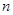 項和
項和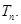
【解析】第一問,因為由題設可知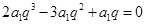
又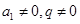 故
故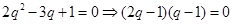
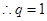 或
或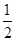 ,又由題設
,又由題設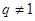
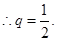 從而
從而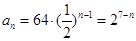
第二問中,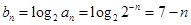
當 時,
時,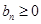 ,
, 時
時
故 時,
時,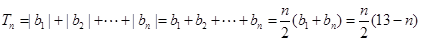
 時,
時,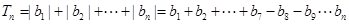
分別討論得到結論。
由題設可知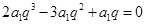
又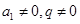 故
故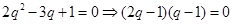
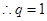 或
或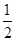 ,又由題設
,又由題設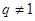
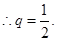
從而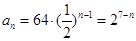 ……………………4分
……………………4分
(2)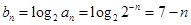
當 時,
時,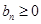 ,
, 時
時 ……………………6分
……………………6分
故 時,
時,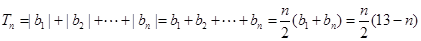 ……8分
……8分
 時,
時,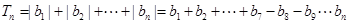
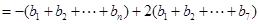
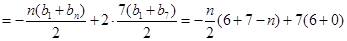
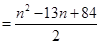 ……………………10分
……………………10分
綜上可得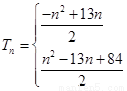

設點 是拋物線
是拋物線

 的焦點,
的焦點, 是拋物線
是拋物線 上的
上的 個不同的點(
個不同的點(
 ).
).
(1) 當 時,試寫出拋物線
時,試寫出拋物線 上的三個定點
上的三個定點 、
、 、
、 的坐標,從而使得
的坐標,從而使得
 ;
;
(2)當 時,若
時,若 ,
,
求證: ;
;
(3) 當 時,某同學對(2)的逆命題,即:
時,某同學對(2)的逆命題,即:
“若 ,則
,則 .”
.”
開展了研究并發現其為假命題.
請你就此從以下三個研究方向中任選一個開展研究:
① 試構造一個說明該逆命題確實是假命題的反例(本研究方向最高得4分);
② 對任意給定的大于3的正整數 ,試構造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
,試構造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
③ 如果補充一個條件后能使該逆命題為真,請寫出你認為需要補充的一個條件,并說明加上該條件后,能使該逆命題為真命題的理由(本研究方向最高得10分).
【評分說明】本小題若填空不止一個研究方向,則以實得分最高的一個研究方向的得分作為本小題的最終得分.
【解析】第一問利用拋物線 的焦點為
的焦點為 ,設
,設 ,
,
分別過 作拋物線
作拋物線 的準線
的準線 的垂線,垂足分別為
的垂線,垂足分別為 .
.
由拋物線定義得到
第二問設 ,分別過
,分別過 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為 .
.
由拋物線定義得


第三問中①取 時,拋物線
時,拋物線 的焦點為
的焦點為 ,
,
設 ,
, 分別過
分別過
 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為
 .由拋物線定義得
.由拋物線定義得




 ,
,
則 ,不妨取
,不妨取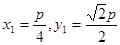 ;
;
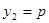 ;
;
 ;
;
解:(1)拋物線 的焦點為
的焦點為 ,設
,設 ,
,
分別過 作拋物線
作拋物線 的準線
的準線 的垂線,垂足分別為
的垂線,垂足分別為 .由拋物線定義得
.由拋物線定義得


因為 ,所以
,所以 ,
,
故可取

 滿足條件.
滿足條件.
(2)設 ,分別過
,分別過 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為 .
.
由拋物線定義得


 又因為
又因為



 ;
;
所以

 .
.
(3) ①取 時,拋物線
時,拋物線 的焦點為
的焦點為 ,
,
設 ,
, 分別過
分別過
 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為
 .由拋物線定義得
.由拋物線定義得




 ,
,
則 ,不妨取
,不妨取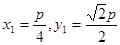 ;
;
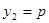 ;
;
 ;
; ,
,
則

 ,
,

 .
.
故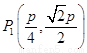 ,
, ,
, ,
, 是一個當
是一個當 時,該逆命題的一個反例.(反例不唯一)
時,該逆命題的一個反例.(反例不唯一)
② 設 ,分別過
,分別過 作
作
拋物線 的準線
的準線 的垂線,垂足分別為
的垂線,垂足分別為 ,
,
由 及拋物線的定義得
及拋物線的定義得
 ,即
,即 .
.
因為上述表達式與點 的縱坐標無關,所以只要將這
的縱坐標無關,所以只要將這 點都取在
點都取在 軸的上方,則它們的縱坐標都大于零,則
軸的上方,則它們的縱坐標都大于零,則






 ,
,
而 ,所以
,所以 .
.
(說明:本質上只需構造滿足條件且 的一組
的一組 個不同的點,均為反例.)
個不同的點,均為反例.)
③ 補充條件1:“點 的縱坐標
的縱坐標 (
( )滿足
)滿足  ”,即:
”,即:
“當 時,若
時,若 ,且點
,且點 的縱坐標
的縱坐標 (
( )滿足
)滿足 ,則
,則 ”.此命題為真.事實上,設
”.此命題為真.事實上,設 ,
,
分別過 作拋物線
作拋物線 準線
準線 的垂線,垂足分別為
的垂線,垂足分別為 ,由
,由 ,
,
及拋物線的定義得 ,即
,即 ,則
,則






 ,
,
又由 ,所以
,所以 ,故命題為真.
,故命題為真.
補充條件2:“點 與點
與點
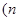 為偶數,
為偶數, 關于
關于 軸對稱”,即:
軸對稱”,即:
“當 時,若
時,若 ,且點
,且點 與點
與點
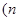 為偶數,
為偶數, 關于
關于 軸對稱,則
軸對稱,則 ”.此命題為真.(證略)
”.此命題為真.(證略)
把函數 的圖象按向量
的圖象按向量 平移得到函數
平移得到函數 的圖象.
的圖象.
(1)求函數 的解析式; (2)若
的解析式; (2)若 ,證明:
,證明: .
.
【解析】本試題主要考查了函數 平抑變換和運用函數思想證明不等式。第一問中,利用設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 ,便可以得到結論。第二問中,令
,便可以得到結論。第二問中,令 ,然后求導,利用最小值大于零得到。
,然后求導,利用最小值大于零得到。
(1)解:設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 證明:令 ,……6分
,……6分
則 ……8分
……8分
 ,∴
,∴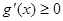 ,∴
,∴ 在
在 上單調遞增.……10分
上單調遞增.……10分
故 ,即
,即
為了解高中一年級學生身高情況,某校按10%的比例對全校700名高中一年級學生按性別進行抽樣檢查,測得身高頻數分布表如下表1、表2.
表1:男生身高頻數分布表
|
身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
|
頻數 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生身高頻數分布表
|
身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
|
頻數 |
1 |
7 |
12 |
6 |
3 |
1 |
(I)求該校男生的人數并完成下面頻率分布直方圖;

(II)估計該校學生身高在 的概率;
的概率;
(III)從樣本中身高在180 190cm之間的男生中任選2人,求至少有1人身高在185
190cm之間的男生中任選2人,求至少有1人身高在185 190cm之間的概率。
190cm之間的概率。
【解析】第一問樣本中男生人數為40 ,
由分層抽樣比例為10%可得全校男生人數為400
(2)中由表1、表2知,樣本中身高在 的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在
的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在 的頻率
的頻率
故由 估計該校學生身高在
估計該校學生身高在 的概率
的概率
(3)中樣本中身高在180 185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185
185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185 190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖,故從樣本中身高在180
190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖,故從樣本中身高在180 190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185
190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185 190cm之間的可能結果數為9,因此,所求概率
190cm之間的可能結果數為9,因此,所求概率
由表1、表2知,樣本中身高在 的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在
的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在
的頻率
 -----------------------------------------6分
-----------------------------------------6分
故由 估計該校學生身高在
估計該校學生身高在 的概率
的概率 .--------------------8分
.--------------------8分
(3)樣本中身高在180 185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185
185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185 190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖為:
190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖為:

--10分
故從樣本中身高在180 190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185
190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185 190cm之間的可能結果數為9,因此,所求概率
190cm之間的可能結果數為9,因此,所求概率
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com