
題目列表(包括答案和解析)
| x-1 |
| x+1 |
|
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 7 |
下列說法,其中正確命題的序號為___ ________.
①.若函數 在
在 處上有極大值,則實數
處上有極大值,則實數 或6
或6
②.對于R上可導的任意函數 ,若滿足
,若滿足 ,則必有
,則必有
③.若函數 在
在 上有最大值,則實數
上有最大值,則實數 的取值范圍為
的取值范圍為
④.已知函數 是定義在R上的奇函數,
是定義在R上的奇函數, ,
,
 ,則不等式
,則不等式 的解集是
的解集是
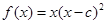 在
在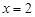 處上有極大值,則實數
處上有極大值,則實數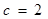 或6
或6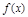 ,若滿足
,若滿足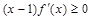 ,則必有
,則必有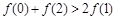
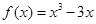 在
在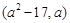 上有最大值,則實數
上有最大值,則實數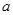 的取值范圍為
的取值范圍為
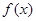 是定義在R上的奇函數,
是定義在R上的奇函數,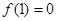 ,
,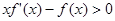
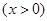 ,則不等式
,則不等式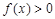 的解集是
的解集是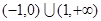
①若a>b,則a2>b2 ②若a>b,則![]() <1 ③若a2>b2且a<0,b<0,則a<b ④a2+b2+ab≥0
<1 ③若a2>b2且a<0,b<0,則a<b ④a2+b2+ab≥0
對于下列結論,其中正確命題的序號是________.
①若a>b,則a2>b2 ②若a>b,則![]() <1 ③若a2>b2且a<0,b<0,則a<b ④a2+b2+ab≥0
<1 ③若a2>b2且a<0,b<0,則a<b ④a2+b2+ab≥0
一、選擇題:每小題5分,共60分
BCCAB ACADB BB
二、填空題:每小題4分,共16分
13. ,甲,甲:
,甲,甲: ①
①
三、解答題:本題滿分共74分,解答應有必要的文字說明,解答過程或演算步驟
17.解:(1)甲、乙二人抽到的牌的所有基本事件(放快4用
(2)甲抽到3,乙抽到的牌只能是2,4,
因此乙抽到的牌的數字大于3的概率是 ;------------------------(6分)
;------------------------(6分)
(3)甲抽到牌比乙大有(3,2),(4,2),(4,3),( ,乙獲勝的與甲獲勝是對立事件,所以乙獲勝的概率是
,乙獲勝的與甲獲勝是對立事件,所以乙獲勝的概率是 ,
,
 此游戲不公平------------------(12分)
此游戲不公平------------------(12分)
18.解:(1)由題意知 .
.

 (5分)
(5分)
 ,
,
 -----------------(7分)
-----------------(7分)
(2)


 -------------------------------------(9分)
-------------------------------------(9分)

 ---------------(12分)
---------------(12分)
19.解:(1) 低面ABCD是正方形,O為中心,
低面ABCD是正方形,O為中心, AC⊥BD
AC⊥BD
又SA=SC, AC⊥SO,又SO
AC⊥SO,又SO BD=0,
BD=0, AC⊥平面SBD-----------------(6分)
AC⊥平面SBD-----------------(6分)
 (2)連接
(2)連接


又由(1)知,AC⊥BD
且AC⊥平面SBD,
所以,AC⊥SB---------------(8分)
 ⊥
⊥
 ⊥
⊥ ,且EM
,且EM NE=E
NE=E
 ⊥平面EMN-------------(10分)
⊥平面EMN-------------(10分)
因此,當P點在線段MN上移動時,總有AC⊥EP-----(12分)
20.解:
 -------------------------------(2分)
-------------------------------(2分)
(2)
則
令 --------------------------------(4分)
--------------------------------(4分)
當x在區間[-1,2]上變化時,y’,y的變化情況如下表:
X
-1



1
(1,2)
2
Y’
+
0
-
0
+
Y
3/2
單增
極大值
單減
極小值
單增
3
又


 -----------(6分)
-----------(6分)
(3)證明:
又


 ---------------------(12分)
---------------------(12分)
21.解:(1)
當
當 ,適合上式,
,適合上式,
 -------------------------------(4分)
-------------------------------(4分)
(2) ,
,
 ①
①
 , ②
, ②
兩式相減,得

=
=
=
 --------------------------------(8分)
--------------------------------(8分)
(3)證明,由

又

=
 成立---------------------------------------------------(12分)
成立---------------------------------------------------(12分)
22.解:(1)由題意可知直線l的方程為 ,
,
因為直線與圓 相切,所以
相切,所以 =1,既
=1,既
從而 ----------------------------------------------------------------------------------------(6分)
----------------------------------------------------------------------------------------(6分)
(2)設 則
則

 ---------------------------------(8分)
---------------------------------(8分)
j當

k當
 故舍去。
故舍去。
綜上所述,橢圓的方程為 ------------------------------------(14分)
------------------------------------(14分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com