題目列表(包括答案和解析)
設P(a,b)（b≠0）是平面直角坐標系xOy中的點，l是經過原點與點(1,b)的直線，記Q是直線l與拋物線x2＝2py（p≠0）的異于原點的交點
⑴.已知a＝1，b＝2，p＝2，求點Q的坐標。
⑵.已知點P(a,b)（ab≠0）在橢圓+y2＝1上，p＝，求證：點Q落在雙曲線4x2－4y2＝1上。
⑶.已知動點P(a,b)滿足ab≠0，p＝，若點Q始終落在一條關于x軸對稱的拋物線上，試問動點P的軌跡落在哪種二次曲線上，并說明理由。
設平面直角坐標系
中，設二次函數
的圖象與坐標軸有三個交點，經過這三個交點的圓記為C。
（1）求實數
的取值范圍；
（2）求圓
的方程；
（3）問圓是否經過某定點（其坐標與無關）？請證明你的結論。
設復數
滿足
，且
在復平面上對應的點在第二、四象限的角平分線上，若
，求和
的值。
設平面直角坐標系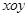
中，設二次函數
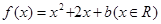的圖象與坐標軸有三個交點，經過這三個交點的圓記為C。
（1）求實數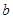
的取值范圍；
（2）求圓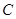
的方程；
（3）問圓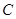是否經過某定點（其坐標與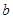無關）？請證明你的結論。
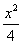+y2=1上，p=
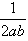，求證：點Q落在雙曲線4x2-4y2=1上；
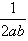，若點Q始終落在一條關于x軸對稱的拋物線上，試問動點P的軌跡落在哪種二次曲線上，并說明理由。 一、選擇題：本大題共10個小題，每小題5分，共50分．
題號
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
B
A
D
B
A
二、填空題：本大題共4個小題，每小題4分，共16分．
11. 630 12. 2k 13. 
14. ①②③
三、解答題：本大題共6個小題，每小題14分，共84分．
15．
(4分) 
由題意得
16． 
有分布列：
0
1
2
3
P
從而期望
17．（1）
又
(2) 
(3)DE//AB,
(4)設BB1的中點為F，連接EF、DF，則EF是DF在平面BB
因為BB
18.(1) 由題意得
(2) 
所以直線
的斜率為
令
，則直線的斜率
，
19．（1）由韋達定理得
是首項為4，公差為2的等差數列。
（2）由（1）知
，則
原式左邊=
=
=右式。故原式成立。
20．令x=y=0，有
，令y=-x則
得
故（1）得證。
（2）在R上任取x1,x2且
，且
，
所以
在R上單調遞增；
（3）
由
得
；
由
得
；因為
，
所以
無解，即圓心到直線的距離大于或等于半徑2，只需
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com