題目列表(包括答案和解析)
（本小題滿分12分）
已知橢圓
經過點
其離心率為
（1）求橢圓
的方程
(2)設直線
與橢圓相交于A、B兩點，以線段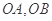
為鄰邊作平行四邊形OAPB，其中頂點P在橢圓上，
為坐標原點. 求到直線
的距離的最小值.
（本小題滿分12分）已知等差數列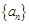
中，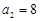
，前10項的和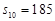
（1）求數列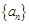的通項公式；
（2）若從數列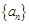中，依次取出第2、4、8，…，
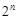，…項，按原來的順序排成一個新的數列
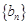，試求新數列
的前
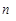項和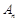
.
（本小題滿分12分）
已知函數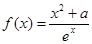
（
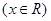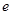是自然對數的底數，
）.
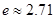（1）當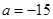
時，求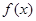
的單調區間；
（2）若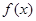在區間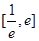
上是增函數，求實數
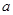的取值范圍；
（3）證明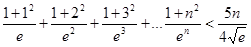
對一切
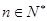恒成立.
（本小題滿分12分）
已知f(x)是R上的奇函數，且當x＞0時，f(x)＝－x2＋2x＋2.
(1)求f(x)的解析式；
(2)畫出f(x)的圖象，并指出f(x)的單調區間．
（本小題滿分12分）
已知等比數列
中，
，求
和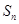
。
一、選擇題（60分）
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
C
B
（C
D
D
A
B
C
B
二、填空題（20分）
13. 15 14．5 15． 
16． 
三、解答題（70分）
17．（1）
，∴
，∴
（5分）
（2）
∵
，∴
，∴
∴
（理10分）
18．
（1）記“甲恰好投進兩球”為事件A，則
（6分）
（2）記“甲比乙多投進兩球”，其中“恰好甲投進兩球且乙未投進”為事件
，“恰好甲投進三球且乙投進一球”為事件
，根據提議，、互斥，
（理12分）
19．（1） （6分）
（2） （文12分）
（3） （理12分）
20．（1）設數列
的公比為
，則
∴
則
（文6分，理4分）
（2）由（1）可知
所以數列
是一個以
為首項，1為公差的等差數列
∴
（文12分，理8分）
（3）∵
∴當
時，
，即
當
時，
，即
綜上可知：時，；時， （理12分）
21. ⑴由已知
所求雙曲線C的方程為
;
⑵設P點的坐標為
,M,N的縱坐標分別為
.
共線
同理
22．
（1）由題意得：
∴在
上
；在
上
；在
上
在此
在
處取得極小值
∴
①
②
③
由①②③聯立得：
∴
（6分）
（2）設切點Q
過
令
，
求得：
，方程
有三個根。
需：
故：
因此所求實數
的取值范圍為：
（理12
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com